गणित
शुल्बसूत्रांमधील भूमिति - एक धावती ओळख. भाग २.
शुल्बसूत्रांमधील भूमिति - एक धावती ओळख. भाग २.
प्रमाणं तृतीयेन वर्धयेत्तच्च चतुर्थेनात्मचतुस्त्रिंशोनेन। सविशेष:।
बौधायन २.१२. इतर शुल्बकारांनीहि जवळजवळ ह्याच शब्दांमध्ये हे मूल्य दाखविले आहे.
सरळ अर्थ - प्रमाण बाजूमध्ये तिचा तिसरा भाग, त्याचा चौथा भाग वाढवावा. त्याचा चौतिसावा भाग कमी करावा. त्यात अजून काही थोडे मिळविले (की इष्ट उत्तर मिळते.)
टिप्पणी - दिलेल्या चौरसाच्या दुप्पट आकाराचा चौरस निर्माण करण्याची पद्धति येथे संक्षिप्तपणाने दर्शविली आहे. अशा दुप्पट आकाराच्या चौरसाची बाजू = मूळच्या चौरसाचा कर्ण हे उघड आहे. मूळ चौरसाच्या बाजूचे प्रमाण = १ असे मानल्यास त्या चौरसाचा कर्ण = वर्गमूळ २. ’२’ चे वर्गमूळ म्हणजे किती हे येथे दर्शविले आहे. ’१ + १/३ + १/३*४ - १/३*४*३४ + थोडेसे वर (सविशेष)’ असे हे ’२’ चे वर्गमूळ दाखविले आहे. आकडेमोड केल्यास १+१/३+१/३*४-१/३*४*३४ = १.४१४२१५६... आणि वर्गमूळ २ = १.४१४२१३... हे पाहिल्यावर असे जाणवते की शुल्बकारांना माहीत असलेले उत्तर खर्या उत्तराच्या खूपच जवळचे आहे. हे उत्तर त्यांनी कसे शोधून काढले असावे?
हा विचार करण्यासाठी शुल्बकारांना उपलब्ध असलेले संख्याज्ञान कशा प्रकारचे होते आणि त्यांचे अंकगणितातील क्रियांचे ज्ञान कशा प्रकारचे होते हे पाहायला लागेल. १, २, ३ अशा नैसर्गिक पूर्ण संख्या, हातापायाच्या १० बोटांवरून १०, १००, १००० अशा संख्या आणि ह्यांच्या संकलनाने (बेरीज) आणि व्यवकलनाने (वजाबाकी) निर्माण होऊ शकणार्या उर्वरित नैसर्गिक पूर्ण संख्या मनुष्यजातीने सहज निरीक्षणामधून निर्माण करून त्या भिन्नभिन्न दर्शविण्यासाठी आवश्यक ती चिह्नेहि निर्माण केली असणे स्वाभाविकच मानता येईल. रोमन संस्कृतीने निर्माण केलेली अशी चिह्ने अजूनहि मर्यादित वापरात आहेत. शुल्बकालीन भारतीयांची अशी चिह्ने काय होती ह्याचा काहीच पुरावा उरलेला नाही, यद्यपि अशी चिह्ने असणार हे निश्चित. तशाच नैसर्गिक विचाराने मोठया समुच्चयाचे एकाच आकाराच्या लहान समुच्चयांमध्ये विभाजन करणे - जसे की १० चे ५ आणि ५ असे दोन बिभाग, १८ चे ६,६,६ असे तीन विभाग - हेहि माहीत असणार. (परंतु १० चे ३ भाग कसे होऊ शकतील हा विचार त्यांच्या झेपेपलीकडील होता.) दोन संख्यांचे संकलन (बेरीज) अथवा त्यांपैकी एकातून दुसरी घालविणे असे व्यवकलन (वजाबाकी) ह्या कृतीहि नैसर्गिकत: सुचणार्या आहेत. मात्र ’शून्य’ ह्या संकल्पनेची निर्मिति आणि तिचा वापर करून संख्येच्या स्थानावरून तिचे मूल्य १० च्या पटीत बदलणे हे ज्ञान अजून काही शतके दूरच होते आणि त्याशिवाय गुणाकार आणि भागाकार हेहि शक्य नव्हते. (रोमन आकडे वापरून गुणाकार करता येत नाही ह्यावरून हे स्पष्ट होईल.) शेती आणि पशुपालन हे मुख्य व्यवसाय असलेल्या आणि संपूर्णत: यन्त्रविरहित असलेल्या समाजाला आपले दैनंदिन जीवन चालविण्यासाठी ह्याहून अधिक गणितज्ञानाची आवश्यकताहि नव्हती.
अशा स्थितीत एका संख्येपासून ज्याला आपण ’वर्ग’ म्हणतो अशी दुसरी संख्या कशी काढायची? उत्तर सरळ आहे. ५ चा वर्ग काढायचा म्हणजे धान्याचे दाणे ५ च्या ओळींमध्ये एकाखाली एक अशा ५ वेळा ठेवायचे आणि एकूण दाणे मोजायचे.
दिलेल्या चौरसाच्या दुप्पट क्षेत्रफळाचा वर्ग कसा काढायचा? दिलेला चौरस शेजारीशेजारी दोन वेळा मांडायचा आणि त्यातील दाणे खालील आकृतीत दाखविल्याप्रमाणे मांडून नवा चौरस मिळतो का हे पाहायचे. आकृतीत ५ इतकी बाजू असलेले दोन चौरस शेजारीशेजारी काढून तेच धान्याचे दाणे वेगळ्या मार्गाने मांडून नवा चौरस मिळतो काय हे पाहण्याचा प्रयत्न केला आहे. असे दिसते की ७ बाजू असलेला नवा चौरस ह्यातून निघतो पण १ दाणा शिल्लक राहतो. हा प्रयोग कोठल्याहि संख्येवर केला तरी सगळे दाणे वापरून नवा चौरस निर्माण करता येत नाही हे लवकरच ध्यानात येते. प्रत्येक वेळी काही दाणे उरतात तरी किंवा कमी पडतात. म्हणजेच केवळ पूर्णांक आणि पूर्ण विभाजन देणारे भागच केवळ वापरून दुप्पट आकाराचा चौरस निर्माण करता येत नाही हे लक्षात येते.
हे नाही तर नाही पण ’सर्वनाशे समुत्पन्ने अर्धं त्यजति पण्डित:’ असा विचार करून सर्वसाधारणत: अदमासाने दुप्पट म्हणता येईल असा चौरस तरी सापडेल काय असा विचार सुरू होतो. त्यासाठी प्रथम एक संख्या घ्यायची, तिच्या चौरसाचे मान काढायचे, त्याची दुप्पट करायची आणि त्या दुपटीच्या जवळ येईल अशी वर्गसंख्या कोठल्या संख्येची आहे असा शोध घ्यायचा. (हे सर्व कार्य वर दिलेल्या अंकगणिताच्या मर्यादेत राहून करणे शक्य आहे.) असे केले म्हणजे (५,७), (१७.२४), (२९,४१), (३४.४८) अशा अनेक जोडया नजरेस येतात पण त्या सर्वांमध्ये एक दोष आहे आणि तो असा की पहिल्या संख्येच्या वर्गाची दुप्पट आणि दुसया संख्येचा वर्ग ह्यांमध्ये बर्यापैकी अंतर आहे आणि ही ढोबळ चूक जितकी पट करू तितक्या प्रमाणात वाढत जाईल. समाधानकारकरीत्या लहान अशी चूक मिळण्यासाठी बरेच पुढे जावे लागेल पण तसे केले की (४०८,५७७) ही जोडी मिळेल जेथे ह्या संख्यांच्या आकारच्या मानाने चूक अगदीच क्षुल्लक आहे. ४०८ चा वर्ग = १,६६,४६४, त्याची दुप्पट ३,३२,९२८ आणि ५७७ चा वर्ग = ३,३२,९२९. म्हणजेच ४०८ प्रमाणक इतकी बाजू असलेला चौरस घेतला तर त्याच्या दुप्पट आकाराच्या चौरसाची बाजू ५७७ पेक्षा अगदी क्षुल्लक फरकाने लहान आहे. हाच ’सविशेष’.
आता प्रश्न येतो की ४०८ प्रमाणक लांबीने प्रारंभ करून आणि वर उल्लेखिलेल्या अंकगणिती मर्यादेत राहून ५७७ प्रमाणक इतकी लांबी कशी मिळवायची. ४०८ चा अर्धा भाग त्याच्या पुढे ठेवला तर आपण ६१२ ला पोहोचतो, जी संख्या ५७७ च्या बरीच पुढे आहे. ४०८ चा तिसरा भाग १३६ त्यापुढे मांडला तर आपण ५४४ ला पोहोचतो. त्या तिसर्या भागाचा चौथा भाग त्यापुढे ठेवला तर आपण ४०८+१३६+३४ = ५७८ ला पोहोचतो. आता आपली उडी ५७७ च्या पुढे १ प्रमाणक इतकी पडली आहे. तो १ (= ४०८ च्या तिसर्या भागाच्या चौथ्या भागाचा चौतिसावा भाग) कमी केला म्हणजे आपण ५७७ ला पोहोचतो. ह्यात ’सविशेष’ मिळवला म्हणजे इष्ट त्या दुप्पट आकाराच्या चौरसाची बाजू मिळेल. वेगळ्या शब्दात लिहायचे तर मूळ चौरसाची बाजू १ प्रमाणक मानली तर इष्ट चौरसाची बाजू =
शुल्बसूत्रांमध्ये वापरलेले लांबीचे कोष्टक ३४ यवाचे दाणे = १ अंगुलि, १२ अंगुलि = १ प्रदेश असे असते. कोष्टकांसाठी साधारणत: निवडले जाणारे २,४,८.१६ असे सोपे आकडे सोडून शुल्बकारांची नजर ३४ वर का पडली असावी ह्याचाहि उलगडा येथे होतो. दिलेल्या चौरसाची बाजू = १ प्रदेश असे मानल्यास इष्ट चौरसाची बाजू आता १ प्रदेश + ५ अंगुलि + १ यव असे मांडता येते. तसे मांडता यावे म्हणून ३२ वा ३६ हे ’सोयीस्कर’ आकडे वगळून तेथे शुल्बकारांनी ३४ यव = १ अंगुलि असे ठरविले असले पाहिजे.
(पहिल्या भागात उल्लेखिलेले थिबो ह्यांचे पुस्तक थोडी वेगळी उपपत्ति देते. तिच्याहून मी येथे दिलेली उपपत्ति अधिक सुकर आहे असे वाटते.)
- Read more about शुल्बसूत्रांमधील भूमिति - एक धावती ओळख. भाग २.
- 8 comments
- Log in or register to post comments
- 5341 views
शुल्बसूत्रांमधील भूमिति - एक धावती ओळख. भाग १.
प्राचीन भारताच्या काळात जे यज्ञ केले जात त्यांचे यज्ञाचे इच्छित फल प्राप्त होण्यासाठी यज्ञ तंतोतंत मुळाबरहुकूम केला जाणे अपेक्षित होते आणि त्यामुळे यज्ञविधीमधील मन्त्रोच्चारण, त्यांचे व्याकरण, शब्दांचे अर्थ कळण्यासाठी व्युत्पत्ति, ऋक्-छन्दांचे ज्ञान, यज्ञास योग्य काळ आणि यज्ञांमधील कृति अशा सहा गोष्टी शिक्षा, व्याकरण, निरुक्त, छन्दस्, ज्योतिष आणि कल्प ह्या सहा निरनिराळ्या वेदांगांनी नियमित केल्या गेल्या आहेत. ह्या सहा वेदांगांपैकी कल्प हे वेदांग नाना यज्ञांचे विधि कसे करावेत हे सांगण्यासाठी निर्माण झाले आहे. कल्पसूत्रांचे मुख्यत: दोन विभाग आहेत. पहिला गृह्यसूत्रे, ज्यांमध्ये व्यक्तींच्या घरांमध्ये होणारे बिवाह, जन्म, मृत्यु अशा प्रकारचे कौटुंबिक विधि कसे केले जावेत हे सांगितले आहे. दुसरा श्रौतसूत्रे, ज्यांमध्ये अधिक मोठे. सार्वजनिक स्वरूपाचे असे विधि (अनेक मन्त्रपाठक आणि अनेक प्रकारचे अग्नि ह्यांच्यासह केले जाणारे) वर्णिले आहेत. ह्यांपैकी यज्ञामधील एक वा अनेक वेदि अथवा चिति कोणत्या आकारांच्या आणि लांबीरुंदीच्या असाव्यात, त्यांचे एकमेकांशी प्रमाण काय असावे असावी हे सांगणे हे शुल्बसूत्रांचे एक प्रमुख कार्य आहे आणि ह्यातूनच आपल्याला वेदकालीन भारतात भूमितिज्ञान किती आणि कशा प्रकारचे होते ह्याची कल्पना येते.
वेदांच्या निरनिराळ्या शाखांशी संलग्न अशी नऊ शुल्बसूत्रे माहीत आहेत. त्यांमध्ये बौधायन, आपस्तम्ब, कात्यायन आणि मानव अशी चार प्रमुख शुल्बसूत्रे आहेत. ’शुल्ब’ अथवा ’शुल्व’ म्हणजे दोरी अथवा रज्जु. यज्ञवेदि बांधण्यासाठी अंतराअंतरावर गाठी बांधलेल्या रज्जूच्या वापराने लांबी मोजणे, वर्तुळ काढणे अशा गोष्टी केल्या जातात. सर्व शुल्बसूत्रांमध्ये प्रारंभी अनेक भौमितिक आकृतींचे आणि त्यांच्या वैशिष्टयांचे वर्णन केले आहे आणि तदनंतर वेदि कशा बांधायच्या ह्याचे विवरण आहे. ह्यावरून शुल्बसूत्र हा शब्द निर्माण झाला आहे. सर्व शुल्बसूत्रांमधून सर्वसाधारणपणे त्याच गोष्टी वेगवेगळ्या शब्दांमधून सांगितल्या आहेत. आधुनिक शब्दात बोलायचे तर शुल्बसूत्रे ही वेदिनिर्माणाचे manual अथवा user-guide आहेत. विशिष्ट आकारांच्या विटांचे काही पातळ्यांपर्यंत थर उभारून आणि त्यांना निरनिराळे आवश्यक आकार देऊन वेदि तयार होतात. काही वेदी त्रिकोण, आयत, चौरस, वर्तुळ अशा सोप्या आकारांच्या असतात तर काही त्याहून थोडया अवघड अशा तुल्यचतुर्भुज - Rhombus, तुल्यलंबक - Trapezium आणि अतुल्यलंबक -Trapezoid - अशा आकारांच्या असतात. श्येन, कूर्म अशा प्राण्यांसारख्या दिसणार्या वेदीहि असतात. त्यांचे क्षेत्रफळ आणि अशा क्षेत्रफळांचे एकमेकात संबंध हे निश्चित केले आहेत. हे सर्व कार्य शास्त्रविहित मार्गाने करण्यासाठी लागणारे भूमितिज्ञान शुल्बसूत्रांमधून मांडण्यात आले आहे.
शुल्बसूत्रांमधील भूमितिज्ञान हे आज आपण शिकतो तशा प्रकारचे म्हणजे गृहीतकृत्ये आणि त्यांमधून तर्काने निघणारी प्रमेये आणि त्यांच्या सिद्धता अशा प्रकारचे नाही. अमुक एक भौमितीय आकार कसा काढावयाचा हे एक स्वत:सिद्ध सत्य म्हणून मांडायचे अशी शुल्बसूत्रांची रचना आहे. केलेल्या विधानाची सिद्धता किंवा ते तसे का ह्याबाबतचे कोठलेच विवेचन त्यात नाही. ह्याचे कारणे असे संभवते की शुल्बसूत्रे हा काही भूमितिशास्त्राचा ग्रंथ नाही. त्यांचे स्वरूप यज्ञविधि करणार्या ऋत्विजांसाठीचे hand-manual अथवा user-guide असे आहे आणि म्हणून त्यात दिलेल्या सूचनांचे शास्त्रीय स्पष्टीकरण तेथे न मिळणे साहजिक आहे.
शुल्बसूत्रांमधील भूमितिज्ञान कसे होते ह्याची काही उदाहरणे आता पाहू. (जमिनीत मेखा - सूत्रांच्या भाषेत शंकु - उभ्या करून आणि त्यांना पुरेशा लांबीच्या रज्जूच्या दोन टोकांनी बांधून एकमेकांशी काटकोन करणार्या दोन रेषा कशा काढायच्या, तसेच वर्तुळ अथवा त्याचा चाप कसा काढायचा, चौरस वा आयत कसा काढायचा अशा स्वरूपाच्या प्राथमिक कृति येथे वगळून पुढे जाऊ. काटकोन अथवा लंब ह्या संकल्पना स्पष्टपणे कोठे उल्लेखिलेल्या दिसत नाहीत पण दिलेल्या कृतींचा परिणाम तोच होतो.)
१)पायथागोरसच्या नावाने ओळखले जाणारे प्रमेय.
दीर्घचतुरस्रस्याक्ष्णयारज्जु: पार्श्वमानी तिर्यङ्मानी च यत्पृथग्भूते कुरुतस्तदुभयं करोति। तासां त्रिकचतुष्कयोर्द्वादशिकपञ्चिकयो: पञ्चदशिकाष्टिकयो: सप्तिकचतुर्विंशिकयोर्द्वादशिकपञ्चत्रिंशिकयो: पञ्चदशिकषट्त्रिंशिकयोरित्येतासूपलब्धि:। बौधायन १.१२.
(येथे दाखविलेले सूत्रांचे संदर्भ ह्या http://hinduonline.co/digitalLibrary.html संस्थळावरील शुल्बसूत्रांच्या देवनागरी आवृत्तीवरून दाखविले आहेत. ही आवृत्ति बर्याच जागी अशुद्ध दिसते पण पुस्तकांच्या digital आवृत्त्यांहून स्पष्ट असल्याने आवश्यक तशी शुद्ध करून तीच वापरली आहे. निरनिराळ्या पुस्तकांमधून सूत्रांचे अनुक्रमांक निरनिराळे दिसतात.)
सरळ अर्थ - आयताचा अक्ष्णयारज्जु ते दोन्ही करतो जे पार्श्वमानी आणि तिर्यङ्मानी वेगवेगळे करतात. ३ आणि ४, १२ आणि ५, १५ आणि ८, ७ आणि २४, १२ आणि ३५, १५ आणि ३६ येथे ही उपलब्धि मिळते.
टिप्पणी - आयताच्या कर्णावर चौरस उभारला तर त्याचे क्षेत्र हे दोन बाजूंवर उभारलेल्या चौरसांच्या क्षेत्रांच्या बेरजेइतके असते. (मुख्य ’प्राची’ म्हणजे म्हणजे पूर्वपश्चिम रेषा. चौरसाची वा आयताची ’प्राची’ला समान्तर असलेली म्हणजेच तिच्या पार्श्वस्थानी असलेली बाजू म्हणजे ’पार्श्वमानी’. तिला लंब करणारी करणारी रेषा ती ’तिर्यङ्मानी’ - चौरसाची वा आयताची आडवी बाजू आणि आयताच्या संदर्भात लहान बाजू. भारतीय पद्धतीने पूर्वपश्चिम रेषा ही उभी - vertical - असते. पूर्व दिशा वर आणि पश्चिम दिशा खाली असते. तिला लंबमान उत्तरदक्षिण रेषा ही आडवी असते. त्यातहि उजवी बाजू ही दक्षिण आणि डावी ही उत्तर. (आठवा - दक्षिणे लक्ष्मणो यस्य वामे च जनकात्मजा - रामरक्षास्तोत्र आणि वामांगी रखुमाई दिसे दिव्य शोभा - पांडुरंगाची आरती.) ’अक्ष्णयारज्जु’ ह्याचा अर्थ चौरसाचा वा आयताचा कर्ण.
काटकोन त्रिकोणाच्या दोन बाजू - भुज आणि कोटि - ह्यांवरील चौरसांच्या क्षेत्राची बेरीज ही कर्णावरील चौरसाच्या क्षेत्राइतकी ह्या पायथागोरसच्या नावाने ओळखल्या जाणार्या प्रमेयाचा तथ्यांश प्राचीन भारतीयांनाहि माहीत होता हे ह्या आणि पुढे दर्शविलेल्या शुल्बसूत्रावरून दिसते. त्याची ’सिद्धता’ भारतात माहीत होती किंवा अशा सिद्धतेची आवश्यकता त्यांना भासली होती असा काही पुरावा आता उरलेला नाही पण तत्त्व माहीत होते हे निश्चित. त्यांना हे कोठून मिळाले अथवा हे भारतातच कोणाला स्वतन्त्रपणे सापडले होते, भारतीयांपाशी हे ज्ञान केव्हापासून होते ह्याचाहि काही पुरावा उरलेला नाही पण त्याचा यज्ञविधींसारख्या बाबीत वापर केला जात होता ह्यावरून भारतीयांना हे स्वतन्त्ररीत्या जाणवले असावे असे मत बनारसच्या संस्कृत कॉलेजातील प्राध्यापक जॉर्ज थिबो ह्यांच्या On the Shulvasutras ह्या १८७५ साली प्रकाशित झालेल्या पुस्तकात व्यक्त करण्यात आले आहे.
२) दिलेल्या चौरसाच्या दुप्पट क्षेत्रफळाचा चौरस निर्माण करणे.
समचतुरस्रस्याक्ष्णयारज्जुर्द्विस्तावतीं भूमिं करोति । बौधायन १.९.
सरळ अर्थ - चौरसाचा कर्ण त्याच्या दुप्पट क्षेत्र निर्माण करतो.
टिप्पणी - समचतुरस्र म्हणजे चारहि बाजू समान असलेला आणि शेजारच्या बाजू एकमेकांस लंब असलेला चौरस. अशा चौरसाचा कर्ण, ज्याला येथे ’अक्ष्णयारज्जु’ असे म्हटलेले आहे, हा बाजू मानून नवा चौरस उभारला तर त्याचे क्षेत्रफळ मूळ चौरसाच्या दुप्पट असते.
३) दिलेल्या चौरसाच्या तिप्पट क्षेत्रफळाचा चौरस निर्माण करणे.
प्रमाणं तिर्यग्द्विकरण्यायामस्तस्याक्ष्णयारज्जुस्त्रिकरणी। बौधायन १.१०.
सरळ अर्थ - रुंदी दिल्याप्रमाणे आणि त्याचा कर्ण आडवी बाजू अशा आयताचा कर्ण तीनपट देतो.
टिप्पणी - दिलेल्या चौरसाच्या बाजूएवढी तिर्यङ्मानी बाजू आणि त्याच्या कर्णाइतकी पार्श्वमानी बाजू असा आयत काढून त्याच्या कर्णावर नवा चौरस बेतला तर त्याचे क्षेत्रफळ मूळच्या चौरसाच्या तिप्पट असेल. ’द्विकरणी’ म्हणजे ’दुप्पट करणारा’ म्हणजेच वर दाखविल्याप्रमाणे चौरसाचा कर्ण. अशा कर्णाइतकी लांबी असलेली पार्श्वमानी बाजू आणि मूळच्या चौरसाच्या बाजूइतकी तिर्यङ्मानी बाजू असलेला आयत काढल्यास तिप्पट क्षेत्राचा चौरस मिळेल.
४) ह्याच मार्गाने पुढे जाऊन मूळ चौरसाहून चौपट, पाचपट इत्यादि कोठल्याहि पटीचे क्षेत्रफळ असलेला चौरस क्रमाक्रमाने करता येईल.
५) मूळ चौरसाच्या कोठल्याहि पटीइतके क्षेत्रफळ असलेला चौरस निर्माण करण्याचा आणखी एक सोपा मार्ग कात्यायन देतो.
 यावत्प्रमाणानि समचतुरस्रस्यैकीकर्तुं चिकीर्षेदेकोनानि तानि भवन्ति तिर्यक् द्विगुणान्येकत एकाधिकानि त्र्यस्रिर्भवति तस्येषुस्तत्करोति। कात्यायन ६.७.
यावत्प्रमाणानि समचतुरस्रस्यैकीकर्तुं चिकीर्षेदेकोनानि तानि भवन्ति तिर्यक् द्विगुणान्येकत एकाधिकानि त्र्यस्रिर्भवति तस्येषुस्तत्करोति। कात्यायन ६.७.
सरळ अर्थ - जितके चौरस एकत्र करावयाचे असतील तेथे आडवी बाजू (चौरसांच्या संख्येच्या) एकाने कमी, (दुसर्या बाजूची) दुप्पट (संख्येहून) एकाने अधिक असा जो (समद्विभुज) त्रिकोण त्याची उंची ते करते.
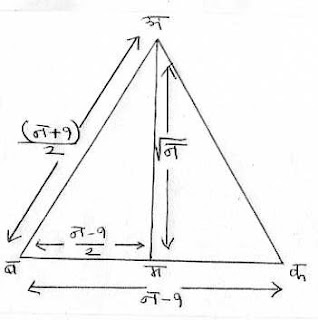
टिप्पणी - दिलेल्या चौरसाच्या ’न’ पट क्षेत्राचा चौरस निर्माण करावयाचा असेल तर असा एक (समद्विभुज) त्रिकोण काढा ज्याचा पाया मूळ चौरसाच्या बाजूच्या ’न - १’ पट असेल आणि एका बाजूची दुप्पट केल्यास ती दुप्पट मूळ चौरसाच्या बाजूच्या ’न + १’ पट असेल, म्हणजेच ती बाजू मूळ चौरसाच्या बाजूच्या ’(न + १)/२’ इतकी पट असेल. अशा त्रिकोणाची उंची (इषु) इष्ट चौरस निर्माण करेल.
शेजारच्या आकृतीत अबक ह्या त्रिकोणात बक = न - १, अम हा ’बक’वर लंब. त्यावरून अम२ = अब२ - बम२ = [(न + १)/२]२ - [(न - १)/२]२ = न. त्रिकोणाची ही उंची अम ही बाजू धरून काढलेल्या चौरसाचे क्षेत्र ’न’ इतके असेल. (येथे मूळ चौरसाची बाजू = १ एकक असे मानले आहे.)
६) चौरसाची जितकी पट करायची ती संख्या अन्य कोठल्या संख्येचा वर्ग असल्यास वापरायचा सोपा मार्ग.
द्विप्रमाणा चतु:करणी त्रिप्रमाणा नवकरणी चतु:प्रमाणा षोडशकरणी। यावत्प्रमाणा रज्जुर्भवति तावन्तस्तावन्तो वर्गा भवन्ति तान्समस्येत्। कात्यायन ३.६, ३.७.
सरळ अर्थ - दुप्पट मापाने चार पट, तिप्पट मापाने नऊ पट, चौपट मापाने सोळा पट )क्षेत्र मिळते.) रज्जु जितका पट तितक्या तितक्या पटीने चौरस. त्यांना एकत्र करावे.
टिप्पणी - मूळ चौरसाच्या दुप्पट बाजू असलेल्या चौरसाचे क्षेत्र मुळाच्या चौपट असते, तिप्पट बाजून नऊ पट आणि चौपट बाजूने सोळा पट क्षेत्र मिळते.
७) एक संख्या दोन वर्गसंख्यांची बेरीज असेल तर त्या संख्येच्या पटीचा चौरस दिलेल्या चौरसापासून निर्माण करणे.
पदं तिर्यङ्मानी त्रिपदा पार्श्वमानी तस्याक्ष्णयारज्जुर्दशकरणी। एवं द्विपदा तिर्यङ्मानी षट्पदा पार्श्वमानी तस्याक्ष्णयारज्जुश्चत्वारिंशत्करणी। कात्यायन २.४, २.५.
सरळ अर्थ - आडवी बाजू एक पट, उभी बाजू तिप्पट तर कर्ण दहा पट निर्माण करतो. तसेच आडवी बाजू दोन पट, उभी बाजू सहा पट. तर कर्ण चाळीस पट निर्माण करतो.
टिप्पणी - दिलेल्या चौरसाच्या बाजूच्या एक पट आडवी बाजू, तीन पट उभी बाजू असा आयत काढल्यास त्याच्या कर्णावरील चौरस मूळ चौरसाच्या दहा पट असेल. दिलेल्या चौरसाच्या बाजूच्या दोन पट आडवी बाजू, सहा पट उभी बाजू असा आयत काढल्यास त्याच्या कर्णावरील चौरस मूळ चौरसाच्या चाळीस पट असेल.
८) वेगवेगळ्या क्षेत्रांच्या दोन चौरसांच्या बेरजेइतक्या क्षेत्राचा चौरस निर्माण करणे.
 नानाचतुरस्रे समस्यन्कनीयस: करण्या वर्षीयसो वृध्रमुल्लिखेत्। वृध्रस्याक्ष्णयारज्जु: समस्तयो: पार्श्वमानी भवति। बौधायन २.१.
नानाचतुरस्रे समस्यन्कनीयस: करण्या वर्षीयसो वृध्रमुल्लिखेत्। वृध्रस्याक्ष्णयारज्जु: समस्तयो: पार्श्वमानी भवति। बौधायन २.१.
सरळ अर्थ - वेगवेगळ्या आकाराचे चौरस एकत्र करू पाहणार्याने लहान चौरसाच्या बाजूइतक्या अंतरावर मोठयाच्या बाजूवर खूण करावी. खुणेपासून काढलेला कर्ण ही (इष्ट) एकत्रित (चौरसाची) बाजू आहे.
टिप्पणी - शेजारच्या आकृतीमध्ये अबकड हा छोटा आणि यरलव हा मोठा चौरस आहेत. यर रेषेवर यम = अब इतके अंतर मोजा. मव ही बाजू धरून काढलेला चौरस हा इष्ट चौरस आहे कारण मव२ = यम२ + यव२ = अब२ + यव२.
९) वेगवेगळ्या क्षेत्रांच्या दोन चौरसांच्या वजाबाकीइतक्या क्षेत्राचा चौरस निर्माण करणे.
चतुरस्राच्चतुरस्रं निजिहीर्षन्यावन्निजिहीर्षेत्तस्य करण्या वर्षीयसो वृध्रमुल्लिखेत्। वृध्रस्य पार्श्वमानीमक्ष्णयेतरत्पार्श्वमुपसंहरेत्। सा यत्र निपतेत्तदपच्छिन्द्यात्। छिन्नया निरस्तम्। बौधायन २.२.
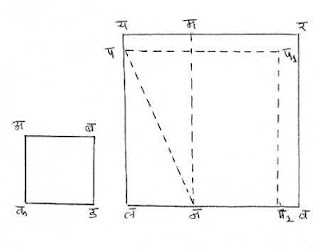 सरळ अर्थ - एका चौरसातून दुसरा चौरस वजा करण्यासाठी ज्यास वजा करायचे आहे त्याच्या बाजूने मोठयाच्या बाजूवर खूण करावी. मोठयातून (आयताकृति) भाग वेगळा काढावा. त्याची उभी बाजू फिरवून (दुसर्या) उभ्या बाजूवर आणावी. ती जेथे पडेल तेथे खूण करावी. ह्या खुणेने कार्य संपते.
सरळ अर्थ - एका चौरसातून दुसरा चौरस वजा करण्यासाठी ज्यास वजा करायचे आहे त्याच्या बाजूने मोठयाच्या बाजूवर खूण करावी. मोठयातून (आयताकृति) भाग वेगळा काढावा. त्याची उभी बाजू फिरवून (दुसर्या) उभ्या बाजूवर आणावी. ती जेथे पडेल तेथे खूण करावी. ह्या खुणेने कार्य संपते.
टिप्पणी - शेजारच्या आकृतीमध्ये अबकड हा छोटा आणि यरलव हा मोठा चौरस आहेत. यर रेषेवर ’म’ बिंदु असा शोधा असा की यम = अब. यमनल हा आयत पुरा करा. ह्या आयताची मन ही बाजू ’न’भोवती फिरवून तिला यल रेषेवरील ’प’पर्यंत आणा. आता पल२ = पन२ - लन२ = मन२ - लन२ = यल२ - अब२. पव ही बाजू धरून निर्माण केलेला पप१प२ल चौरस हा इष्ट चौरस होय जो तुटक रेषेने दाखविला आहे.
१०) दिलेल्या आयताच्या क्षेत्राचा चौरस करणे.
दीर्घचतुरस्रं समचतुरस्रं चिकीर्षंस्तिर्यङ्मानीं करणीं कृत्वा शेषं द्वेधा विभज्य विपर्यस्येतरत्रोपदध्यात्। खण्डमावापनेन तत्संपूरयेत्। तस्य निर्हार उक्त:। बौधायन २.५.
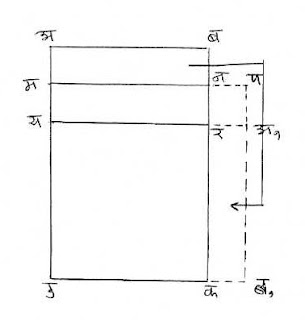 सरळ अर्थ - आयताचा चौरस करू इच्छिणार्याने आडव्या रेषेला बाजू मानून (त्यावर चौरस करावा). (आयताच्या) उर्वरित भागाचे दोन भाग पाडून (एकाला) उलटून बाजूस लावावे. (उरलेला) खंड (चौरस) तुकडयाने भरून घ्यावा. त्यांची वजाबाकी आधी सांगितली आहे.
सरळ अर्थ - आयताचा चौरस करू इच्छिणार्याने आडव्या रेषेला बाजू मानून (त्यावर चौरस करावा). (आयताच्या) उर्वरित भागाचे दोन भाग पाडून (एकाला) उलटून बाजूस लावावे. (उरलेला) खंड (चौरस) तुकडयाने भरून घ्यावा. त्यांची वजाबाकी आधी सांगितली आहे.
टिप्पणी - शेजारच्या आकृतीत अबकड हा दिलेला आयत आहे. त्याच्या डक ह्या तिर्यङ्मानीवर (आडव्या आखूड बाजूवर) यरकड हा चौरस उभारा. उरलेल्या अबरय ह्या भागाचे अबनम आणि मनरय असे दोन समान भाग करा. अबनम भागाला रमअ१ब१क असे दक्षिण बाजूस उभे लावा. मूळचा आयत आता मनरअ१ब१ड अशा अनियमित आकारामध्ये संक्रमित झाला आहे. त्याच्या कोपर्यावर उरलेल्या चौरस आकाराच्या खंडाला नपअ१र असे नाव द्या.
आता मपब१ड हा चौरस आहे हे स्पष्ट आहे. त्यामधून नपअ१र ह्या चौरसाला वजा केले असता उरलेल्या क्षेत्राचा चौरस कसा निर्माण करावयाचा हे वर क्र.९ मध्ये दर्शविले आहे. त्या मार्गाने इष्ट चौरस निर्माण करा.
११) पार्श्वमानी तिर्यङ्मानीहून बरीच मोठी असल्यास अशा आयताचा चौरस करण्यासाठी सोपा मार्ग.
अतिदीर्घश्चेत्तिर्यङ्मान्याऽपच्छिद्यापच्छिद्यैकसमासेन समस्य शेषं यथायोगमुपसंहरेदित्येक: समास:। कात्यायन ३.३.
सरळ अर्थ - आयत अतिदीर्घ असल्यास तिर्यङ्मानीने (आखूड बाजूने) पार्श्वमानीवर शक्य तेवढे छेद घेऊन चौरस करावेत आणि त्यांचा वर क्र. ५ मध्ये दिल्याप्रमाणे एक चौरस करावा. उरलेल्या आयताकृति भागाचा क्र. १० मध्ये दिल्याप्रमाणे चौरस करावा. दोन्ही नवे चौरस क्र. ८ प्रमाणे जोडून इष्ट चौरस होईल.
१२) चौरसामधून त्याच क्षेत्राचा आयत करणे.
समचतुरस्रं दीर्घचतुरस्रं चिकीर्षंस्तदक्ष्णयाऽपच्छिद्य भागं द्वेधा विभज्य पार्श्वयोरुपदध्याद्यथायोगम्। बौधायन २.३.
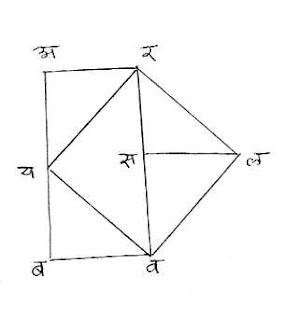 सरळ अर्थ - चौरसाचा (त्याच क्षेत्राचा) आयत करण्यार्याने कर्णाने चौरसाचे दोन भाग करून त्यामधील एका भागाचे दोन भाग करून ते (दुसर्या) भागाच्या दोन बाजूंवर बसवावे.
सरळ अर्थ - चौरसाचा (त्याच क्षेत्राचा) आयत करण्यार्याने कर्णाने चौरसाचे दोन भाग करून त्यामधील एका भागाचे दोन भाग करून ते (दुसर्या) भागाच्या दोन बाजूंवर बसवावे.
टिप्पणी - शेजारच्या आकृतीत दर्शविल्याप्रमाणे यरलव ह्या चौरसाचे रव ह्या कर्णाने दोन भाग केले. नंतर रलव ह्या भागाचे रलस आणि वलस असे दोन भाग केले. रलव उचलून यर शेजारी लावला, जेणेकरून रल ही रेषा यर ह्या रेषेवर पडेल. तसेच वलस ह्या भागाचे केले. आता अरवब हा आयत मिळाला ज्याचे क्षेत्र मूळ चौरसाइतके आहे.
१३)दिलेल्या चौरसाइतक्या क्षेत्राचा आणि एक बाजू दिलेली असणारा आयत निर्माण करणे.
अपि वै तस्मिँश्चतुरस्रं समस्य तस्य करण्यापच्छिद्य यदतिशिष्यते तदितरत्रोपदध्यात्। बौधायन २.४.
सरळ अर्थ - त्या (चौरसावर) (दिलेल्या बाजूचा) आयत निर्माण करून त्याच्या कर्णाने छेदून जे उरते ते इतरत्र ठेवावे.
ह्यावरून फारसा बोध होत नाही कारण सूत्र फार त्रोटक आहे. बिभूतिभूषण दत्ता ह्यांनी सौन्दरराज आणि द्वारकानाथ यज्वा ह्या टीकाकारांच्या टीकांचा आधार घेऊन पुढील अर्थ दिला आहे.
’यावदिच्छं पार्श्वमान्यौ प्राच्यौ वर्धयित्वा उत्तरपूर्वां कर्णरज्जुमायच्छेत्। सा दीर्घचतुरस्रमध्यस्थायां समचतुरस्रतिर्यङ्मान्यां यत्र निपतति तत उत्तरं हित्वा दक्षिणांशं तिर्यङ्मानीं कुर्यात्। तद्दीर्घचतुरस्रं भवति।’ ह्याचा अर्थ असा: (चौरसाच्या) दोन पार्श्वमानी बाजू पूर्वेकडे इष्ट लांबीपर्यंत वाढवून (आणि तो आयत पूर्ण करून) त्याची उत्तरपूर्व कर्णरेषा काढा. ती कर्णरेषा चौरसाच्या तिर्यङ्मानी बाजूस जेथे छेदेल तेथून उत्तर बाजू सोडून देऊन दक्षिण बाजू ही (इष्ट आयताची) तिर्यङ्मानी बाजू करा. असा (इष्ट)आयत निर्माण होईल.
प्रारंभीच म्हटल्याप्रमाणे भारतीय पद्धतीने वर पूर्व, डावीकडे उत्तर आणि उजवीकडे दक्षिण हे येथे लक्षात ठेवले पाहिजे.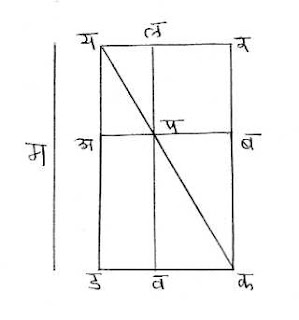 शेजारच्या आकृतीवरून ही कृति स्पष्ट होते. अबकड हा दिलेला चौरस आहे आणि म ही इष्ट आयताची लांबी आहे. (त्यामुळे म > अब हे स्पष्ट आहे.) डअ आणि कब ह्यारेषा अनुक्रमे य आणि र पर्यंत इतक्या वाढवा की यड = रक = म. यरकड हा आयत पूर्ण करा. त्याची यक ही कर्णरेषा अब ह्या अबकड चौरसाच्या तिर्यङ्मानीला जेथे छेदते त्या बिंदूस प असे नाव द्या. लपव ही यडला समान्तर रेषा काढा, ती अशी की ल आणि व हे बिंदु अनुक्रमे यर आणि कड ह्या रेषांवर असतील. लपव रेषेच्या उत्तरेकडील म्हणजे डाव्या बाजूचा भाग सोडला तर उरलेला आयत लरकव हा इष्ट आयत आहे.
शेजारच्या आकृतीवरून ही कृति स्पष्ट होते. अबकड हा दिलेला चौरस आहे आणि म ही इष्ट आयताची लांबी आहे. (त्यामुळे म > अब हे स्पष्ट आहे.) डअ आणि कब ह्यारेषा अनुक्रमे य आणि र पर्यंत इतक्या वाढवा की यड = रक = म. यरकड हा आयत पूर्ण करा. त्याची यक ही कर्णरेषा अब ह्या अबकड चौरसाच्या तिर्यङ्मानीला जेथे छेदते त्या बिंदूस प असे नाव द्या. लपव ही यडला समान्तर रेषा काढा, ती अशी की ल आणि व हे बिंदु अनुक्रमे यर आणि कड ह्या रेषांवर असतील. लपव रेषेच्या उत्तरेकडील म्हणजे डाव्या बाजूचा भाग सोडला तर उरलेला आयत लरकव हा इष्ट आयत आहे.
हे विधान असे ताडून पाहता येते: त्रिकोण यलप + चौकोन लरबप + त्रिकोण पबक = त्रिकोण यपअ + चौकोन अपवड + त्रिकोण पकव. आता त्रिकोण यलप = त्रिकोण यपअ आणि त्रिकोण पबक = त्रिकोण पकव. ह्यावरून चौकोन लरबप = चौकोन अपवड. म्हणून चौकोन लरबप + चौकोन पबकव = चौकोन अपवड + चौकोन पबकव, म्हणजेच आयत लरकव = चौरस अबकड.
(भाग २ मध्ये पुढे चालू. भाग २ मध्ये वर्तुळापासून चौरस बनविणे, ’२’ ह्या संख्येचे वर्गमूळ असे विषय असतील.)
आधार -
1) Ancient Hindu Geometry - Bibhutibhushan Datta,
2) The Shulvasutras - George Thibaut,
3) Ancient Indian Mathematics and Vedha - Laxman Vishnu Gurjar.
माहितीमधल्या टर्म्स
- Read more about शुल्बसूत्रांमधील भूमिति - एक धावती ओळख. भाग १.
- 11 comments
- Log in or register to post comments
- 9235 views
ट्रोजन युद्ध भाग २.२- इलियडमधले द्रोणपर्व: विविध वीरांचा पराक्रम आणि अकीलिसचा धुमसता राग.
धाग्याचा प्रकार निवडा:
माहितीमधल्या टर्म्स
गणित म्हणजे काय?
गणितात प्रवीण मुलांपैकीही फारच थोड्यांना गणितात गोडी असते, बाकी सगळे गणिताकडे उत्तम गुण मिळवून देणारा विषय, म्हणजे एक दुभती गाय, याच दृष्टीने बघत असतात. वर्गातील बहुसंख्य मुलांना तर गणिताची भीतीच वाटत असते. अशा परिस्थितीत गणिताकडे कसे पाहावे? गणित कसे शिकवावे? गणिताची नावड कशी घालवता येईल?
धाग्याचा प्रकार निवडा:
माहितीमधल्या टर्म्स
- Read more about गणित म्हणजे काय?
- 5 comments
- Log in or register to post comments
- 3092 views
सममित आकृतींचा शोध - भाग ३
तीन मितींच्या अवकाशातच थांबून राहणे गणितज्ञांना रुचत नाही. चार किंवा उच्चतर मितींच्या विश्वातील सुसम आकृती शोधू पाहिल्या तर गणिती जगतातील एक अद्भुत असमतोल सापडतो.
माहितीमधल्या टर्म्स
- Read more about सममित आकृतींचा शोध - भाग ३
- 3 comments
- Log in or register to post comments
- 1480 views
सममित आकृतींचा शोध - भाग २
दोन मितींच्या प्रतलावर, म्हणजे कागदावर, पूर्णतः सममित अशा वेगवेगळ्या आकाराच्या अनंत चित्राकृती काढता येतात. तीन मितींच्या अवकाशात पूर्णतः सममित अशा किती घनाकृती बनवता येतात?
माहितीमधल्या टर्म्स
- Read more about सममित आकृतींचा शोध - भाग २
- 6 comments
- Log in or register to post comments
- 2184 views
सममित आकृतींचा शोध - भाग १
एकाचसारखे दिसणारे अनेक भाग सुसूत्रपणे जोडून एखादी आकृती बनली असेल तर ती सममित (symmetric) असते. प्राचीन काळापासून मानवप्राणी सममित आकृतींकडे आकृष्ट झाला आहे. अशा सममित आकृतींचा शोध घेणारी एक लघुलेखमाला.
माहितीमधल्या टर्म्स
- Read more about सममित आकृतींचा शोध - भाग १
- 5 comments
- Log in or register to post comments
- 2590 views
पायथागोरसचे प्रमेय - भाग ३
सरळ रेषा एक मितीची, प्रतल दोन मितींचे आणि जिथे आपला वावर असतो ते अवकाश तीन मितींचे असे आपण मानतो. मग यापेक्षा जास्त म्हणजे चार मितींचे विश्व कसे असेल? आणि त्यातले पायथागोरसचे प्रमेय कसे असेल?
माहितीमधल्या टर्म्स
- Read more about पायथागोरसचे प्रमेय - भाग ३
- 8 comments
- Log in or register to post comments
- 2294 views
पायथागोरसचे प्रमेय - भाग २
पहिल्या भागात पाहिलेले पायथागोरसचे प्रमेय आयताच्या किंवा काटकोन त्रिकोणाच्या कर्णासंबंधी आहे. या दोन्ही आकृती दोन मिती असलेल्या प्रतलावर काढता येतात. तीन मिती असलेल्या अवकाशात या द्विमितीय प्रमेयाची दोन वेगवेगळी प्रतिरूपे होऊ शकतात.
माहितीमधल्या टर्म्स
- Read more about पायथागोरसचे प्रमेय - भाग २
- 2 comments
- Log in or register to post comments
- 1395 views
पायथागोरसपेक्षा पोदयनार सरस?
पायथागोरसचे प्रमेय – भाग १ हा लेख संपवण्याच्या बेतात होतो तेवढ्यात कुणी निनावी माणसाने मला एक निरोप अग्रेसर (Forward) केला, कायप्पा (व्हॉट्सॅप, WhatsApp) या तत्काळ संदेश पाठवणाऱ्या सेवेवरून. निरोपाचे शीर्षक होते : 'कर्णाची लांबी शोधून काढण्याची वैकल्पिक पद्धत'! मी साशंक झालो, आपल्या लेखात बदल करावा लागणार की काय अशा काळजीने.
माहितीमधल्या टर्म्स
- Read more about पायथागोरसपेक्षा पोदयनार सरस?
- 17 comments
- Log in or register to post comments
- 3912 views
