गणिताच्या निमित्ताने – भाग ७
गणिताच्या निमित्ताने – भाग ७
बालमोहन लिमये
(भौतिक-रसायनादि शास्त्रांप्रमाणेच गणितातही नव्या अनुभवजन्य शोधांमुळे सिद्धांतांत सुधारणा करावी लागते का? आणि, मी माझ्या पत्नीला म्हटले, ‘निर्मला, कल्याणीच्या तोंडातून युक्लिड बोलतोय!’ – प्राध्यापक बालमोहन लिमये यांच्या साप्ताहिक लेखमालेतील पुढील भाग. मागील भाग इथे.)
भूमिति आणि सापेक्षता
आय. आय. टी.मधील माझ्या सुरुवातीच्या काही वर्षांत गणित, भौतिकी (Physics) आणि रसायन (Chemistry) या तीन विभागांतील काही प्राध्यापक मंडळींनी एक ‘सैद्धांतिक अभ्यासमंडळ’ (Group of Theoretical Studies, उर्फ GTS) स्थापन केले. रसायन विभागातील प्रा. बी. एम. देब यांनी पुढाकार घेतला होता. भौतिकी विभागातील प्रा. सी. आर. शर्मा, प्रा. जी. एस. मूर्ति, आणि गणित विभागातील मी व इतर एक-दोघे दर आठवड्याला एकत्र जमत असू, चर्चा करत असू, कधी कोणी सेमिनार देत असे. आय. आय. टी.च्या निदेशकांनी या कार्यक्रमासाठी एका छोट्या रकमेचे प्रावधानही केले होते. आमच्यापैकी कोणी लिहिलेल्या शोधनिबंधावर आपापल्या विभागाखेरीज GTS अशी आमची संलग्नता (affiliation) दाखवायचेही आम्ही ठरवले होते.
एका दिवशी या अभ्यासमंडळात भूमिती आणि भौतिकी यांच्यातील परस्परसंबंधाबद्दल चर्चा चालू होती. परंपरागत भूमितीचे भौतिकशास्त्रामधील पायाभूत स्वरूप सर्वांना ठाऊक होते, पण आधुनिक भूमिती आधुनिक भौतिकीमध्ये काय भूमिका बजावते याबद्दल सुस्पष्टता नव्हती. कोणी तरी म्हणाले की नव्या अनुभवजन्य शोधांमुळे गणिताच्या सिद्धांतांत सुधारणा करावी लागते. आइन्स्टाइनची सापेक्षता (relativity) ही संकल्पना मांडण्यासाठी पुराणी भूमिती सोयीची नव्हती म्हणून तिला डच्चू देऊन ती बदलावी लागली. हे काही मला मानवले नाही, कारण गणितातील सिद्धांत फक्त आधीच सांगून ठेवलेल्या गृहीतकांवर अवलंबून असतात. जोपर्यंत आपण ती गृहीतके बदलत नाही तोपर्यंत ते अबाधित राहतात आणि ते कुठल्याही प्रयोगांच्या आधारावर बदलावे लागत नाहीत याची मला खात्री होती. परंतु मी त्यावेळी जास्त काही बोललो नाही. पुढच्या आठवड्यात चांगले वाचन करून मगच गणितावरील टीकात्मक विधानांचा समाचार घ्यायचे मी ठरवले.
आपण शाळेत शिकतो ती भूमिती इसवी सनापूर्वी सुमारे तीनशे वर्षे युक्लिड (Euclid) या ग्रीक गणितज्ञाने लिहिलेल्या ‘Elements’ नावाच्या प्रख्यात ग्रंथावर आधारलेली असते. असे म्हणतात की बायबल सोडले तर या पुस्तकाच्या सर्वात अधिक आवृत्ति प्रकाशित झाल्या आहेत. ते कसेही असो, युक्लिडचे हे पुस्तक गणिताच्या निगमन पद्धतीचे (deductive method) आद्य व सर्वोत्कृष्ट उदाहरण आहे. युक्लिड सुरुवातीला पाच गृहीतके (postulates) मांडतो व त्यावरून भूमितीचा सगळा डोलारा कसा उभारता येतो ते दाखवून देतो. बिंदू, रेषा आणि प्रतल यांच्या व्याख्या न करता ते शब्द अव्याख्यात (undefined) ठेवायचे. पाच गृहीतकांपैकी पहिली चार अगदी सोपी आहेत. उदाहरणार्थ, पहिले गृहीतक आहे: ‘एका बिंदूपासून दुसऱ्या बिंदूपर्यंत सरळ रेषा काढता येते.’ अशीच आणखी तीन आहेत, पूर्णपणे स्वयंसिद्ध वाटणारी. परंतु युक्लिडचे पाचवे गृहीतक जरा वेगळे आहे. स्कॉटिश शास्त्रज्ञ जॉन प्लेफेअर (John Playfair) याच्या शब्दात ते जास्त सुलभपणे सांगता येते. तत्पूर्वी असे नोंदवू या की समांतर रेषा म्हणजे एकाच प्रतलातील पण एकमेकींना न छेदणाऱ्या रेषा. पाचवे गृहीतक असे आहे :
‘एक सरळ रेषा व तिच्यावर नसणारा एक बिंदू दिला असल्यास त्या बिंदूतून जाणारी आणि त्या रेषेला समांतर असणारी एकच सरळ रेषा असते.’
हे गृहीतक वापरूनच आपण शाळेत असताना दाखवलेले असते की त्रिकोणाच्या तीन कोनांची बेरीज 180 अंश झाली पाहिजे. ह्या पाचव्या गृहीतकाला ‘समांतर गृहीतक’ (Parallel Postulate) असे म्हणतात. युक्लिडला आणि त्याच्या नंतरच्या कित्येक गणितज्ञांना वाटत होते की हे पाचवे गृहीतक पहिल्या चार गृहीतकांच्या सहाय्याने सिद्ध करता आले पाहिजे. पण ते काम कोणीच करू शकला नाही. सरतेशेवटी, ज्याला सर्वांत महान गणिती समजले जाते त्या कार्ल फ्रीड्रिश गाउस (Carl Friedrich Gauss) याने १८१८च्या सुमाराला युक्लिडच्या पाचव्या गृहीतकाच्या ऐवजी एक मुलखावेगळे गृहीतक मांडले. ते असे:
‘एक सरळ रेषा व तिच्यावर नसणारा एक बिंदू दिला असल्यास त्या बिंदूतून जाणाऱ्या आणि त्या सरळ रेषेला समांतर असणाऱ्या अनेक सरळ रेषा असतात.’
आता आपण असे म्हणू शकतो की हे गृहीतक मानले तरी प्रत्यक्षात अशा अनेक समांतर रेषा दिसत तर कुठेच नाहीत. इथेच तर मोठी गोम आहे. प्रत्यक्ष अनुभवाला चिकटून राहिलेच पाहिजे असे बंधन गणितज्ञावर नसते. तो एवढेच सुनिश्चित करतो की आपण मानलेली गृहीतके एकमेकांशी सुसंगत आहेत ना. मग अशा सुसंगत गृहीतकांवर आधारलेली सिद्धांतांची इमारत तो रचतो आणि त्या इमारतीच्या सौंदर्यांत हरखून जातो. गाउसने हेच केले, पण त्याने आपले याबाबतचे सिद्धांत लिहून ठेवले नाहीत, आणि जरी ते कधी काळी लिहिले तरी मरेपर्यंत प्रसिद्ध न करण्याचे त्याने ठरवले होते.
१८२० ते १८२३ च्या दरम्यान एक तरुण हंगेरियन गणिती यानोश बोय्याई (János Bolyai) युक्लिडच्या पाचव्या गृहीतकाबरोबर झगडत होता. त्याला कळून चुकले होते की हे पाचवे गृहीतक आधीच्या चार गृहीतकांवर अवलंबून नाही, आणि ते जर मानलेच नाही तर वेगळ्या घाटणीच्या भूमिती व तिच्यातील सिद्धांत मिळू शकतात. पण त्याचे संशोधन १८३२ पर्यंत प्रसिद्ध झाले नाही, आणि झाले तेसुद्धा त्याच्या वडिलांनी लिहिलेल्या पुस्तकाचे एक परिशिष्ट म्हणून. हे परिशिष्ट वाचल्यावर गाउस खूष झाला, पण म्हणाला ‘या कामाची स्तुती करणे म्हणजे माझीच स्तुती करण्यासारखे आहे, कारण याच गोष्टी मी गेली कित्येक वर्षे मनांत साठवून ठेवल्या होत्या.’

निकोलाय लोबाचेव्हस्की
परंतु ख्याती कुणाला मिळेल आणि किती मिळेल हे काही सांगवत नाही. यानोशला काही पत्ता नसलेला दुसरा एक तरुण गणिती रशियात कार्यरत होता. त्याचे नाव होते निकोलाय लोबाचेव्हस्की (Nikolai Lobachevsky). त्याने आपले संशोधन १८२९ साली म्हणजे यानोसच्या आधी दोन-तीन वर्षे प्रसिद्ध केले. त्यांत निकोलायने स्वतंत्रपणे नव्या भूमितीची मांडणी केली होती, अगदी गाउसप्रमाणेच युक्लिडचे समांतर गृहीतक बदलून.
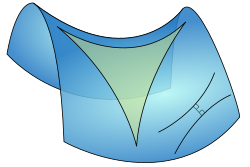
अपास्तपृष्ठावरील त्रिकोण
शिवाय त्याने ‘समांतरतेचा कोन’ (Angle of Parallelism) ही संकल्पना प्रस्तुत केली. या भूमितीत अपास्ताभाच्या पृष्ठभागावरील (surface of hyperboloid) त्रिकोणाच्या तीन कोनांची बेरीज 180 अंशांपेक्षा कमी असते. लोबाचेव्हस्कीने जे संशोधन केले होते त्याचा यानोशला १८४८ पर्यंत पत्ताही नव्हता! सध्या या भूमितीला Lobachevsky Geometry किंवा अपास्तीय भूमिती (Hyperbolic Geometry) म्हणतात, किंवा कधी कधी Bolyai-Lobachevsky Geometry असेही संबोधतात.
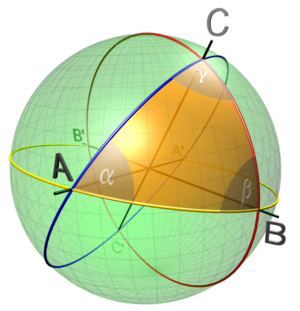
गोलीय पृष्ठभागावरील त्रिकोण
पुढे बेर्नहार्ड रीमान (Bernhard Riemann) याने त्याच्या १८५४ सालच्या गाजलेल्या व्याख्यानात एक सोपी भूमिती प्रस्तुत केली. तिला विवृत्तीय भूमिती (Elliptic Geometry) असे म्हणतात. या भूमितीत त्याने युक्लिडचे समांतर गृहीतक अगदी दुसऱ्या टोकाला नेले. ते असे :
‘एक सरळ रेषा व तिच्यावर नसणारा एक बिंदू दिला असल्यास त्या बिंदूतून जाणारी आणि त्या रेषेला समांतर असणारी एकही सरळ रेषा नसते.’
या भूमितीत पोकळ गोलावरील त्रिकोणाच्या तीन कोनांची बेरीज 180 अंशांपेक्षा जास्त होते.
युक्लिडच्या समांतर गृहीतकाचे अशा दोन प्रकारे प्रतियोजन (replacement) केल्याबद्दल अपास्तीय भूमिती (Hyperbolic Geometry) आणि विवृत्तीय भूमिती (Elliptic Geometry) या दोन्ही भूमितींना अयुक्लिडीय भूमिती (Non-Euclidean Geometry) अशी संज्ञा प्राप्त झाली. भूमितीबद्दलची ही परिस्थिति चटकन लक्षात यावी म्हणून तशाच प्रकारचे पण अगदी वेगळ्या संदर्भातील एक उदाहरण देता येईल. ख्रिस्ती, यहुदी किंवा मुस्लीम धर्मांचे अनुयायी असे गृहीत धरतात की देव एकच असतो, मग भले यापैकी एका धर्माचा देव इतर धर्मांच्या देवांसारखा असो वा नसो. उलटपक्षी हिंदू धर्माचे काही अनुयायी अनेक देव गृहीत धरायला तयार असतात, तर बौद्ध धर्माचे अनुयायी देवच नाही असे गृहीत धरतात. आपापल्या गृहीतकांवरून त्या त्या धर्माच्या चालीरीती, पद्धती ठरून जातात; गृहीतक बदलले की चालीरीती बदलतात, नाहीतर नाही.
या सगळ्यावरून स्पष्ट होते की गणितज्ञांनी केवळ आपली जिज्ञासा शमवण्यासाठी युक्लिडच्या भूमितीपेक्षा वेगळी भूमिती सुमारे दोनशे वर्षांपूर्वी शोधून काढली होती, भले तिचा प्रत्यक्षाशी संबंध असो वा नसो. विसाव्या शतकाच्या सुरुवातीला जेव्हा लोरेन्ट्झ (Lorentz), प्वाँकारे (Poincare), आइन्स्टाइन वगैरे मंडळींकडून सापेक्षतावादाची बांधणी होत होती, तेव्हा युक्लिडचीच भूमिती वापरायची ठरवली तर दोन सापेक्ष वेगांची बेरीज किंवा संघटन (Addition or Composition of Relative Velocities) कशी करायची याबाबत नेहमीपेक्षा वेगळे नियम किंवा वेगळी सूत्रे बनवावी लागली. याच सुमारास मिन्कोव्हस्कीने (Minkowsky) चार मितींच्या अवकाश-कालाची (four dimensional space-time) संकल्पना प्रस्तुत केली आणि सापेक्षतावादाची मजबुती केली, पण तीही युक्लिडच्या भूमितीच्या अंतर्गतच.
१९१० साली व्ह्लादिमिर व्हारिचाक (Vladimir Varicak) या युगोस्लाव्हियातील गणितज्ञाने एक वेगळीच शक्कल लढवली. त्याला बोय्याई आणि लोबाचेव्हस्की यांनी संकल्पिलेली अपास्तीय भूमिती (Hyperbolic Geometry) माहीत होती. त्याने दाखवले की युक्लिडच्या अवकाशात काम न करता जर आपण लोबाचेव्हस्कीच्या अवकाशाचा उपयोग केला तर दोन सापेक्ष वेगांचे संघटन फार सोप्या प्रकारे करता येते, आणि म्हणून विशिष्ट सापेक्षतेसाठी (Special Relativity) लोबाचेव्हस्कीची भूमिती वापरणे सयुक्तिक ठरते. व्हारिचाक आणि त्याच्या अनुयायांचे म्हणणे फार प्रचलित झाले नाही, कारण एक तर त्या काळात लोबाचेव्हस्कीची विचित्र भूमिती अनेकांना झेपत नव्हती, आणि दुसरे म्हणजे थोड्याच वर्षांनी १९१५ साली आइन्स्टाइनची सामान्य सापेक्षतेची (General Relativity) संकल्पना प्रामुख्याने समोर आली व व्हारिचाकने केलेली विशिष्ट सापेक्षतेची मांडणी मागे पडली.

व्ह्लादिमिर व्हारिचाक
मुख्य मुद्दा हा की युक्लिडच्या भूमितीला जराही धक्का लागला नव्हता. ती पूर्णपणे शाबूत होती. त्या भूमितीपेक्षा वेगळी भूमिती गणितज्ञांनी आधीच उभारून ठेवली होती. ती युक्लिडच्या भूमितीपेक्षा जास्त गुंतागुंतीची होती हे खरे, पण नेमक्या याच भूमितीचा उपयोग झाला एका सापेक्षतावादातील वैज्ञानिक उपपत्तीला सोपे करून देण्यात. आय. आय. टी.मधील आम्ही प्राध्यापक मंडळींनी चालवलेल्या सैद्धांतिक अभ्यासमंडळाच्या पुढल्या बैठकीत हे सगळे विशद केल्यावरच मला हायसे वाटले.
मूळ संख्या सतत मिळत जातील का?
1, 2, 3, 4, ... यांना म्हणतात नैसर्गिक संख्या (natural numbers). अशी एखादी संख्या जर 1 पेक्षा मोठी असेल आणि तिला दुसऱ्या कुठल्याच संख्येने (1 वगळता) भाग जात नसेल, तर तिला ‘मूळ संख्या’ किंवा ‘अविभाज्य संख्या’ (prime number) असे नाव देतात. उदाहरणार्थ, 2, 3, 5, 7, 11, 13 मूळ संख्या आहेत, अगदी सुरुवातीला येणाऱ्या. आपण प्राथमिक शाळेत शिकतो की कुठलीही नैसर्गिक संख्या काही मूळ संख्यांचा गुणाकार करून मिळवता येते, आणि त्या मूळ संख्यांना दिलेल्या संख्येचे ‘मूळ अवयव’ (prime factors) म्हणतात, जसे 12 = 2 × 2 × 3 किंवा 35 = 5 × 7, आणि म्हणून 12 या संख्येचे 2, 2 व 3 हे मूळ अवयव आहेत, तर 35 या संख्येचे 5 व 7 हे मूळ अवयव आहेत.
माझी मोठी मुलगी कल्याणी मुंबईतील आय. आय. टी.च्या परिसरातील सेंट्रल बोर्डाच्या शाळेत जात असे. ती पाचवीत असताना एके दिवशी घरी आल्यावर म्हणाली ‘बाबा, आज आम्हाला मूळ संख्या कशाला म्हणतात ते शिकवले.’ मी तिला मूळ संख्यांची उदाहरणे विचारली. तिने मला पहिल्या दहा मूळ संख्या सांगितल्या. मी तिला सहज प्रश्न केला, ‘कल्याणी, अशा मूळ संख्या सतत मिळत जातील का केव्हा तरी संपून जातील?’ कल्याणीने जेमतेम मिनिटभर विचार केला आणि म्हणाली, ‘बाबा, मोठमोठ्या मूळ संख्या मिळतच राहतील.’ मी म्हटले ‘कशावरून म्हणतेस असे?’ तिने तत्काळ उत्तर दिले, ‘बाबा, असे बघ, समज एकूण शंभरच मूळ संख्या आहेत. मग त्या सगळ्या शंभर मूळ संख्यांचा मी गुणाकार करेन आणि त्यांत 1 मिळवेन. ही जी नवीन संख्या तयार होईल, तिला आपल्याजवळच्या शंभर मूळ संख्यांपैकी एकीनेही भाग जाणार नाही, आणि म्हणून त्या संख्या या नवीन संख्येचे मूळ अवयव असू शकत नाहीत. मग या संख्येचे मूळ अवयव कुठून आणायचे? याचा अर्थ असा होतो की आपल्याजवळच्या शंभर मूळ संख्यांशिवाय आणखीही काही मूळ संख्या असल्याच पाहिजेत, म्हणजे एकूण मूळ संख्या शंभरपेक्षा जास्त असणार.’
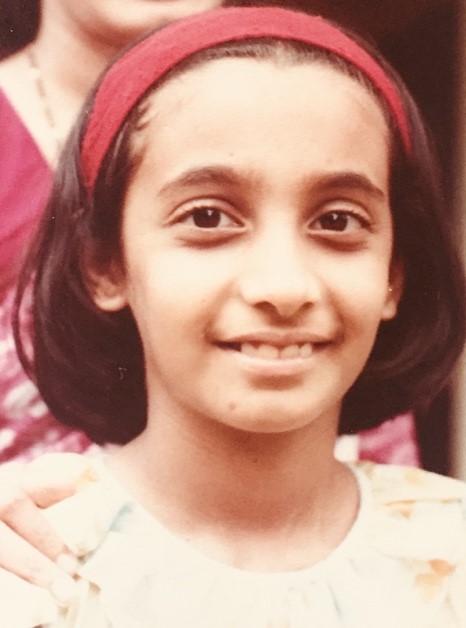
कल्याणी, १९८२
हे उत्तर ऐकून मी अवाक झालो. कल्याणीला अनंतता (infinity) ही संकल्पना माहीत नव्हती, पण तिच्या युक्तिवादात तिने वापरलेल्या शंभर या आकड्याऐवजी दुसरा कोणताही आकडा वापरता आला असता. त्यामुळे असे सिद्ध होते की मूळ संख्या सीमित किंवा सान्त (finite) नाहीत, त्या अनंत (infinite) असल्या पाहिजेत. इसवी सनापूर्वी जवळ जवळ ३०० वर्षे ग्रीसमधील युक्लिडने मूळ संख्यांच्या अनंततेची हीच विरोधजन्य सिद्धता (proof by contradiction) दिली होती. मी माझ्या पत्नीला म्हटले, ‘निर्मला, कल्याणीच्या तोंडातून युक्लिड बोलतोय!’ खरोखर, गणितातील निरनिराळ्या उत्तम सिद्धांतांच्या ज्या काही सुंदर, सोप्या सिद्धता उपलब्ध आहेत त्यांपैकी ही एक आहे. ख्यातनाम गणिती पॉल एर्डिश म्हणत की कोणी तरी एक खास पुस्तक (The Book) लिहिलेले आहे, आणि त्यात असे सगळे उत्तम सिद्धांत आणि अशा सुंदर सिद्धता आधीच लिहून ठेवलेल्या आहेत. पण तो लेखक पक्का हुकुमशहा (Supreme Fascist) असल्याने त्याच्या मर्जीनुसार मधूनमधून तो आपल्याला त्या पुस्तकाचे एखादे पान बघू देतो!
युक्लिडने दिलेल्या सिद्धतेमध्ये आपण उपलब्ध असलेल्या ज्या काही मूळ संख्या उपलब्ध आहेत त्यांचा गुणाकार करतो व त्यात 1 मिळवतो. आपण सुरुवातीपासूनच्या मूळ संख्यांचा गुणाकार करून त्यात 1 मिळवत गेलो, तर या नव्याने बनवलेल्या सगळ्या संख्या मूळ संख्याच असतील का? जरा तपासून पाहू या. आता 2 + 1 = 3, (2 × 3) + 1 = 7, तसेच (2 × 3 × 5) + 1 = 31, (2 × 3 × 5 × 7) + 1 = 211 आणि (2 × 3 × 5 × 7 × 11) + 1 = 2311 या सगळ्या मूळ संख्या आहेत. म्हणजे वरपांगी तरी असे दिसते की आपल्या प्रश्नाचे उत्तर होकारार्थी असावे. पण इतके उतावळे होऊन चालत नाही. यानंतरची संख्या (2 × 3 × 5 × 7 × 11 × 13) + 1 = 30031 ही मूळ संख्या नाही, कारण 30031 = 59 × 509. म्हणजे आपल्या प्रश्नाचे उत्तर नकारार्थी आहे. यावरून दोन गोष्टी लक्षात येतात. एक म्हणजे विश्वासार्ह अनुमान (conjecture) बांधायला भरपूर आणि खोल निरीक्षणांची गरज असते. दुसरी गोष्ट म्हणजे सुरुवातीपासूनच्या मूळ संख्यांचा गुणाकार करून त्यात 1 मिळवणे हा नवनवीन मूळसंख्या निर्माण करण्याचे सूत्र (formula) होऊ शकत नाही. वस्तुतः असे कुठलेच सूत्र अद्यापि सापडलेले नाही. डिसेंबर २०२० पर्यंत सापडलेली सर्वात मोठी मूळ संख्या आहे 282,589,933 - 1; ती लिहून काढली तर 24,862,048 अंकी होईल.
मोठमोठ्या मूळ संख्यांचा एक अगदी अनपेक्षित उपयोग सध्या केला जात आहे. गूढलेखन (Cryptography) या क्रियेत आपण पाठवलेला संदेश ज्याच्यासाठी आहे त्यालाच समजावा, इतर कुणाला समजू नये याची खबरदारी घ्यावी लागते. आपण दोन मोठ्या मूळ संख्या मनाशी बाळगू आणि ज्याला संदेश पाठवायचा आहे त्याला त्या सांगून ठेवू. या मूळ संख्यांचा गुणाकार करून जी अवाढव्य संख्या मिळेल, तीच फक्त सांकेतिक (coded) संदेश पाठवताना वापरायची. ही अवाढव्य संख्या इतरांना कळली तरी हरकत नाही, कारण संदेशातील संकेत समजण्यासाठी (decoding) आपण घेतलेल्या मूळ संख्या माहित असणे जरूर असते व त्या इतर कुणाला शोधून काढणे अशक्य कोटीतले असते. म्हणून आपला संदेश केवळ इच्छित माणसालाच समजू शकतो. उदाहरणार्थ, 193,707,721 आणि 761,838,257,287 या मूळ संख्यांचा गुणाकार करणे तसे सोपे आहे, निदान संगणकाला तरी; तो गुणाकार आहे 267 – 1. आता 267 – 1 या अवाढव्य संख्येला फक्त वरील दोनच मूळ अवयव आहेत, व नुसती 147,573,952,589,676,412,927 ही 21 आकड्यांची संख्या बघून ते अवयव शोधून काढणे संगणकालाही सोपे नाही. म्हणून आपला संदेश आपण ज्याला ते मूळ अवयव आधीच सांगून ठेवले असतील त्यालाच समजू शकतो. मूळ संख्यांचा असा व्यावहारिक उपयोग पाहून बहुतेक सगळ्यांना हायसे वाटेल. परंतु प्राध्यापक जी. एच. हार्डी या मूळ संख्यांबाबत मूलगामी संशोधन केलेल्या शुद्ध गणितज्ञाला (pure mathematician) चक्क वाईट वाटत असे. ते म्हणायचे, ‘अरेरे, निव्वळ कुतूहल शमवण्यासाठी आपण केलेले प्रयास अशा गौण गोष्टी साध्य करण्यास वापरले जावेत, यापरते दुःख नाही!’
मूळ संख्यांबाबत समजायला अगदी सोपी पण गमतीदार माहिती पाहू या. एखादी मूळ संख्या सम असू शकते का? जवळजवळ कधीच नाही, कारण 2 सोडून कुठल्याच मूळ संख्येला 2 ने भाग जाणे शक्य नाही. म्हणून 2 ही एकच मूळ संख्या सम आहे आणि बाकीच्या सर्व मूळ संख्या विषम आहेत. याच कारणास्तव दोन मूळ संख्या एकामागून एक (consecutive) येऊ शकत नाहीत, फक्त 2 आणि 3 हा अपवाद सोडता. हे फारच सोप्या रीतीने सिदध करता येईल. समजा p आणि p + 1 या दोन्ही मूळ संख्या आहेत. या दोन संख्यांपैकी एक संख्या सम असली पाहिजे आणि एक संख्या विषम असली पाहिजे. पण जर एखादी मूळ संख्या सम असेल, तर ती मूळ संख्या 2 च असली पाहिजे, आणि p + 1 ही संख्या 2 असू शकत नाही. अशाप्रकारे p = 2, आणि म्हणून p + 1 = 3. आता थोडे पुढे जाऊन असे विचारूया की दोन मूळ संख्या एक सोडून एक येऊ शकतात का, म्हणजे p आणि p + 2 या दोन्ही मूळ संख्या असू शकतात का? जरा तपासून पाहिले, तर आपल्याला अशा खूप जोड्या मिळतील. उदाहरणार्थ, (3, 5), (5, 7), (11, 13), (17, 19) वगैरे. अशा जोडगोळी असलेल्या मूळ संख्यांना ‘जुळ्या मूळ संख्या’ (twin primes) असे म्हणतात.
एकूण सगळ्या मूळ संख्या अनंत असतात हे आपण आताच पाहिले. आता विचारता येईल की जुळ्या मूळ संख्यासुद्धा अनंत आहेत की कांही टप्प्यानंतर त्या मिळायच्या बंद होतात? हा प्रश्न मी कल्याणीला विचारला नाही. तसे विचारणे रास्त झाले नसते, कारण सन १८५० पासून जगातील किती तरी गणितज्ञ त्याचे उत्तर शोधत आहेत. तरीही तो प्रश्न आज अनिर्णित आहे, म्हणजे आजतागायत कोणी असे सिद्ध केलेले नाही की जुळ्या मूळ संख्या अनंत आहेत, आणि कोणी असेही दाखवलेले नाही की एका मर्यादेपलीकडे या जोडगोळ्या मिळत नाहीत. जर कोणी या दोन गोष्टींपैकी एक गोष्ट पुराव्यानिशी मांडली तर त्याला क्षणार्धात ख्याती मिळेल, आणि गडगंज पैसाही. या प्रश्नावर काम करणाऱ्या सगळ्यांचा कयास मात्र असा आहे की मोठमोठ्या जुळ्या मूळ संख्या नेहमी मिळत राहतील, त्या कधीच संपणार नाहीत. या कयासाचे नाव ‘जुळ्या मूळ संख्यांचे अनुमान’ (Twin Prime Conjecture) असे आहे. आजपर्यंत सापडलेल्या सर्वात मोठ्या जुळ्या मूळ संख्या आहेत 2996863034895 × 21290000 – 1 आणि 2996863034895 × 21290000 + 1.
क्षणभर जुळ्या मूळ संख्यांकडून तिळ्या मूळ संख्यांकडे जाऊ या. p, p + 2, p + 4 या तिन्ही मूळ संख्या असू शकतात का? याचे उत्तर मात्र सोपे आहे, कारण p, p + 1 आणि p + 2 या लागोपाठ येणाऱ्या तीन संख्यापैकी एकीला तीनने भाग गेला पाहिजे. आता p + 4 = (p + 1) + 3 असल्याने p + 1 ला तीनने भाग जाणे याचाच अर्थ p + 4 ला तीनने भाग जाणे असा होतो. अशाप्रकारे आपण म्हणू शकतो ही p, p + 2, p + 4 या संख्यांपैकी एकीला तीनने भाग गेला पाहिजे. पण जर एखाद्या मूळ संख्येला 3 ने भाग गेला तर ती मूळ संख्या 3 च असली पाहिजे, आणि p + 2 किंवा p + 4 ही संख्या 3 असू शकत नाही. अशाप्रकारे p = 3 आणि म्हणून (3, 5, 7) हे एकच तिळे शक्य आहे. जरा बदल करून असे विचारले की p, p + 2 आणि p + 6 या तिन्ही मूळ संख्या असू शकतात का, तर अशा त्रिकूटांची किती तरी उदाहरणे मिळतील. उदाहरणार्थ, (5, 7, 11), (11, 13, 17), (17, 19, 23), (41, 43, 47), (101, 103, 107) वगैरे. पण अशी मूळ संख्यांची त्रिकूटे अनंत आहेत की नाहीत हे मात्र अजून कुणालाच ठाऊक नाही. ती जर अनंत असली, तर मात्र जुळ्या मूळ संख्यासुद्धा अनंत असतात हे ओघानेच आले.
आणखी एक मजेदार निरीक्षण सांगतो. कुठलीही 2 पेक्षा मोठी सम संख्या घेतली, तर असे दिसते की ती कुठल्यातरी दोन मूळ संख्यांची बेरीज करून मिळवता येते, जसे 12 = 5 + 7, 100 = 11 + 89, 102 = 13 + 89 वगैरे. ही गोष्ट प्रथम जर्मन गणितज्ञ ख्रिश्चियन गोल्डबाख (Christian Goldbach) याच्या लक्षात आली. त्याने स्विस गणितज्ञ लिओन्हार्ड ऑयलर (Leonhard Euler) याच्याशी १७४२ साली याबाबत पत्रव्यवहार केला होता. या निरीक्षणाची शहानिशा करायची असली तर असे सिद्ध करता आले पाहिजे की प्रत्येक 2 पेक्षा मोठी सम संख्या नेहमीच दोन ठिकाणी विभागता येते जेणेकरून प्रत्येक भाग एक मूळ संख्या असेल, किंवा उलटपक्षी एक तरी 2 पेक्षा मोठी सम संख्या शोधता आली पाहिजे की जी या प्रकारे विभागता येणार नाही. आजपर्यंत खूप गणितज्ञांनी अतोनात प्रयत्न करूनही याचा निर्णय होऊ शकलेला नाही. मात्र सगळ्यांचा अंदाज असा आहे की गोल्डबाखने केलेले निरीक्षण कधी ना कधी सिद्ध करता येईल. म्हणून त्याला ‘गोल्डबाखचे अनुमान’ (Goldbach Conjecture) असे म्हणतात. आतापर्यंत 4 आणि 4 × 1018 यामधील प्रत्येक सम संख्या दोन मूळ संख्यांची बेरीज करून मिळवता येते असे संगणकाच्या साह्याने दाखवता आले आहे. हा आकडा केवढा मोठा आहे याची कल्पना येण्यासाठी आपण लक्षात घेऊ या की एका शास्त्रीय अंदाजाप्रमाणे आपल्या विश्वाचे वय 1018 सेकंदांपेक्षा कमी आहे. पण तरीही गोल्डबाखचे अनुमान खरे आहे की खोटे आहे हे आपण नक्की सांगू शकत नाही.

ख्रिश्चियन गोल्डबाख
ग्रीक लेखक अपोस्तोलो दोक्सिआदिस (Apostolos Doxiadis) याने २००० साली ‘पेत्रोस काका आणि गोल्डबाखचे अनुमान’ (Uncle Petros and Goldbach Conjecture) या नावाची कादंबरी लिहिली. ती आंतरराष्ट्रीय स्तरावर ‘बेस्ट सेलर’ म्हणून गाजली आणि पस्तीस भाषांत प्रसिद्ध झाली. कादंबरीच्या ब्रिटीश व अमेरिकन प्रकाशकांनी जर कोणी दोन वर्षांच्या आत गोल्डबाखचे अनुमान सिद्ध केले तर त्याला दहा लाख डॉलर्सचे बक्षिस जाहीर केले होते. ही जाहिरातबाजी तर होतीच, पण यावरून गोल्डबाखचे अनुमान किती आकर्षक आहे हे कळून येते.
एखादा कठीण प्रश्न सोडवता आला नाही तरी गणितज्ञ सहजासहजी हार मानायला तयार नसतात. मग ते मूळच्या प्रश्नापेक्षा जरा सोपा प्रश्न सोडवायचा प्रयत्न करतात. अशा सुलभीकरणाचा एक मार्ग असा असतो. मूळच्या अनुमानाचे उत्तर होकारार्थी आहे असे समजून जर त्यातून एखादे विधान निष्पन्न होत असेल, तर मूळच्या अनुमानापेक्षा हे नवीन विधान सिद्ध करणे सोपे जावे. कुठलीही 2 पेक्षा मोठी सम संख्या दोन मूळ संख्यांची बेरीज असते या अनुमानाचे उत्तर होकारार्थी आहे असे समजले, तर कुठलीही 5 पेक्षा मोठी विषम संख्या तीन मूळ संख्यांची बेरीज होणार हे विधान निष्पन्न होते. याचे कारण असे. समजा m ही 5 पेक्षा मोठी विषम संख्या आहे. मग m - 3 ही 2 पेक्षा मोठी सम संख्या होते, आणि जर आपण p आणि q अशा मूळ संख्या मिळवल्या की m - 3 = p + q, तर m ही संख्या 3 + p + q अशा तीन मूळ संख्यांची बेरीज होते. उदाहरणार्थ, 103 – 3 = 100 = 11 + 89, व म्हणून 103 = 3 + 11 + 89. हे लक्षात घेऊन अनेक गणितज्ञांनी असे सिद्ध करायचा प्रयत्न केला की कुठलीही पाचपेक्षा मोठी विषम संख्या तीन मूळ संख्यांची बेरीज असते. तेही अवघड होते, पण २०१३ साली हाराल्ड हेल्फगॉट (Harald Helfgott) या पेरू देशाच्या गणितज्ञाला ते साध्य झाले.

हाराल्ड हेल्फगॉट, २०१५
हेल्फगॉटने गणिती युक्तिवाद वापरून असे दाखवले की जर एखादी विषम संख्या 1027 पेक्षा मोठी असेल तर ती तीन मूळ संख्यांची बेरीज असली पाहिजे, आणि संगणकाच्या साह्याने असेही दाखवले की 7 आणि 1029 यामधील प्रत्येक विषम संख्या तीन मूळ संख्यांची बेरीज करून मिळवता येते. यामुळे आता आपण ठामपणे म्हणू शकतो की पाचपेक्षा मोठी प्रत्येक विषम संख्या तीन मूळ संख्यांची बेरीज असते. एका विषम संख्येतून 3 वजा करून जशी आपण एक सम संख्या मिळवली, तसेच एका सम संख्येतून 3 वजा करून आपण एक विषम संख्या मिळवू शकतो, व हेल्फगॉटचे प्रमेय वापरून असे म्हणू शकतो की आठपेक्षा मोठी प्रत्येक सम संख्या चार मूळ संख्यांची बेरीज असते. शिवाय 8 = 2 + 2 + 2 + 2, म्हणजे आठ ही संख्यादेखील चार मूळ संख्यांची बेरीज आहेच. यामुळे सहापेक्षा मोठी प्रत्येक सम संख्या चार मूळ संख्यांची बेरीज असते असे सिद्ध होते. जवळजवळ दोनशे सत्तर वर्षांनी गोल्डबाखचे अनुमान सिद्ध करण्यात गणितज्ञांना असे अंशत: यश मिळाले.
विषम आणि सम अशा दोन्ही प्रकारच्या संख्यांचा विचार करून असे निष्पन्न होते की 1 पेक्षा मोठी प्रत्येक संख्या जास्तीत जास्त चार मूळ संख्यांची बेरीज करून मिळू शकते; जर गोल्डबाखचे अनुमान कधी काळी सिद्ध झाले तर जास्तीत जास्त तीनच मूळ संख्यांची बेरीज करून काम भागेल. मूळ संख्यांच्या गुणाकाराबाबत मात्र आपण असे काहीच म्हणू शकत नाही. 1 पेक्षा मोठी कुठलीही संख्या तिच्या मूळ अवयवांचा गुणाकार असते हे खरे, पण ती अमुक इतक्याच मूळ संख्यांचा गुणाकार करून मिळवता येईल असे बिलकुल नाही; यासाठी किती मूळ संख्या लागतील याला सीमा नाही, जसे 6 = 2 × 3 साठी दोन मूळ संख्यांचा गुणाकार करावा लागतो, तर 30 = 2 × 3 × 5 साठी तीन, 210 = 2 × 3 × 5 × 7 साठी चार, 2300 = 2 × 3 × 5 × 7 × 11 साठी पाच, तर 30030 = 2 × 3 × 5 × 7 × 11 × 13 साठी सहा मूळ संख्यांचा गुणाकार करावा लागतो, आणि असे करत गेले तर आपल्याला कधीच थांबता येणार नाही, कारण मूळ संख्या सतत मिळत राहतात ना! आहे की नाही गंमत!
(पुढील भाग)
---
बालमोहन लिमये
(balmohan.limaye@gmail.com)

लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण
ललित लेखनाचा प्रकार
सरळ रेषा
निरनिराळ्या भूमितींत 'सरळ रेषा' ह्याचा अर्थ 'अल्पांतरी' म्हणजे geodesic ही मूलभूत संकल्पना वापरून लावावा लागतो हे नमूद करावेसे वाटते. लेखात उल्लेख केलेल्या तीनही भूमितींत दोन 'समांतर' सरळ रेषा म्हणजे एकमेकींना न छेदणार्या (त्या त्या भूमितींतल्या) दोन सरळ रेषा असा लावला पाहिजे. लेख छानच आहे. Goldbach चे शब्दलेखन (spelling) सुरुवातीलाच चुकून Golbach असे झाले आहे. तसेच Harald चा उच्चार हॅरल्ड असा नको का? अजून काही सापडते का ते बघतो. :-)
अंतर मम
> निरनिराळ्या भूमितींत 'सरळ रेषा' ह्याचा अर्थ 'अल्पांतरी' म्हणजे geodesic ही मूलभूत संकल्पना वापरून लावावा लागतो हे नमूद करावेसे वाटते.
ह्यात तथ्य नक्कीच आहे, आणि लेखात आलेल्या उदाहरणांबाबत हे खरं आहे. पण माझ्या अनुभवाप्रमाणे हे सगळीकडे लागू होत नाही. जी काही भूमिती समोर असेल तिच्यात दरवेळी ‘अंतराचं मोजमाप’ (metric) ही संकल्पना असलीच पाहिजे असं नाही. उदाहरणार्थ, प्रोजेक्टिव्ह जॉमेट्रीमध्ये (काही ठराविक गृहीतकांच्या बंधनात राहून) कशाला बिंदू म्हणायचं आणि कुठल्या रेषेत कुठले बिंदू असणार हे आपण यदृच्छेने ठरवू शकतो. बिंदूंची एकूण संख्या सांत असू शकते (७, १३ वगैरे), आणि दोन बिंदूंतलं अंतर किती हा प्रश्न तिथे उद्भवत नाही.
+ (माझेही दोन पैसे) (FWIW)
लेख छानच आहे.
याच्याशी सहमत.
निरनिराळ्या भूमितींत 'सरळ रेषा' ह्याचा अर्थ 'अल्पांतरी' म्हणजे geodesic ही मूलभूत संकल्पना वापरून लावावा लागतो हे नमूद करावेसे वाटते. लेखात उल्लेख केलेल्या तीनही भूमितींत दोन 'समांतर' सरळ रेषा म्हणजे एकमेकींना न छेदणार्या (त्या त्या भूमितींतल्या) दोन सरळ रेषा असा लावला पाहिजे.
यावरून एक गोष्ट आठवली.
फारा वर्षांपूर्वी माझा एक जुना पारशी मित्र बाहेरगावाहून मला भेटायला आला. माझ्याच घरी उतरला. उतरला तो उतरला, परंतु, त्यानंतर मग जे काही दोनतीन दिवस माझ्या घरी होता, तेवढ्यात त्याने त्याचे जे जे म्हणून जुने कॉलेजकालीन वगैरे (आणि माझ्याशी यत्किंचितही संबंध नसलेले) मित्र माझ्या गावात होते, त्यांना सर्वांना एक एक करून त्याला भेटण्यासाठी माझ्या घरी बोलावण्याचा सपाटा लावला. तेही ठीकच म्हणा.
तर असाच एके संध्याकाळी त्याचा एक मुसलमान मित्र त्याला भेटायला म्हणून माझ्या घरी आला. चहापाणी वगैरे झाले. अचानक त्याचा तो मुसलमान मित्र, माझ्या घरात एखादी मोकळी खोली वगैरे काही मिनिटांकरिता त्याला खाजगीमध्ये, वैयक्तिक वापरासाठी मिळू शकेल काय, म्हणून विचारू लागला. का, तर म्हणे त्याची प्रार्थनेची वेळ झाली, म्हणून. म्हटले, ठीक आहे. त्याला एक विशेष वापरात नसलेली खोली दाखवून दिली, नि म्हटले बस तिथे; तिथे तुला कोणीही डिस्टर्ब करणार नाही, म्हणून.
मग पुढचा प्रश्न: इथून ईशान्य म्हणजे नक्की कोठल्या बाजूला राहिली, म्हणून. का, तर म्हणे प्रार्थना करताना मक्केकडे तोंड करावे लागते.
ईशान्य?????? अटलांटात बसून मक्केकडे बोले तो ईशान्येकडे?????? मी बुचकळ्यात पडलो. परंतु, "असेल बुवा. मला काय करायचेय?" म्हणून मी तो विषय तेवढ्यावरच सोडून त्याला माझ्या अंदाजाप्रमाणे ईशान्य दिशा दाखवली.
माझ्या पारशी मित्रालाही खरे तर हाच प्रश्न पडला होता. परंतु, मिनिटभर गहन विचार केल्यावर त्याची ट्यूब पेटली, नि "अरे यार! वो ग्रेट सर्कल-वाला फंडा!!!" म्हणून त्याने खुलासा केला.
----------
मला वाटते, गोलपृष्ठीय भूमितीचे प्रतलीय भूमितीवर प्रोजेक्शन (मराठी? प्रक्षेपण???) करून विचार करण्याच्या सवयीमुळे आपल्या अशा बऱ्याच गोच्या होत असाव्यात. बऱ्याच गोष्टी लक्षात येत नसाव्यात. उदाहरणार्थ:
१. सर्व रेखावृत्ते ही 'सरळ रेषा' आहेत; उलटपक्षी, विषुववृत्त वगळल्यास एकही अक्षवृत्त हे 'सरळ रेषा' नाही.
२. अक्षवृत्ते ही 'समांतर रेषा' नाहीत. (अर्थात, विषुववृत्त वगळल्यास बाकीची अक्षवृत्ते ही मुळात 'रेषा'च नाहीत, म्हटल्यावर...)
३. (शंका: मुळात गोलीय पृष्ठभागावरील कोठल्याही दोन 'रेषा' या कधी समांतर असूच शकतात काय?)
४. कॉंट्ररी टू इंट्यूशन/पॉप्युलर पर्सेप्शन, (उदाहरणादाखल) न्यूयॉर्कहून हाँगकाँग किंवा सिंगापूरला जाण्यासाठी सर्वात जवळचा मार्ग हा सपाट कागदावरील नकाशावर सरळ रेषा काढून वाटते त्याप्रमाणे आग्नेयेकडे (अटलांटिक + युरोप + आशिया पालथा घालून) किंवा नैर्ऋत्येकडे (आख्खी खंडीय संयुक्त संस्थाने + पॅसिफिक ओलांडून + कदाचित पूर्व आशियाला थोडाफार स्पर्श करून) नसून, उत्तर ध्रुवाच्या बऱ्यापैकी जवळून जावा. किंवा, ऑस्ट्रेलियातील पर्थहून आर्जेंटिनातील बुएनोस आयरेसला जाणारा सर्वात जवळचा मार्ग हा सरळसरळ पश्चिमेकडे न जाता, अंटार्क्टिकावरून (आणि बहुधा दक्षिण ध्रुवाच्या बऱ्यापैकी जवळून) जावा. (हे पाहा.) अर्थात, ध्रुवांजवळून विमाने उडविण्यात अनेक व्यावहारिक/लॉजिस्टिकल (मराठी?) अडचणी येत असल्याकारणाने हे फारसे कोणी करीत नसावे. (अधिक माहितीकरिता हे आणि हेदेखील पाहा.)
५. यावरून, लहानपणी ऐकलेले एक कोडे आठवले.
एकदा एक शिकारी, बंदूक घेऊन शिकारीच्या शोधात निघतो. शिकार शोधत शोधत, निघाल्या ठिकाणाहून एक मैल दक्षिणेस जातो. तेथून एक मैल पूर्वेस जातो. तेथून एक मैल उत्तरेस जातो. तेथे त्याला एक अस्वल दिसते, ते तो टिपतो. नंतर, टिपलेले अस्वल निघाल्या ठिकाणी परत कसे न्यावे, याचा विचार करीत असताना त्याच्या लक्षात येते, की, अरे, आपण निघाल्या ठिकाणीच आहोत की! आपल्याला काहीच करण्याची गरज नाही! तर, त्याने टिपलेल्या अस्वलाचा रंग कोणता?
या कोड्याचे उत्तर 'पांढरा' असे आहे. कारण, (कोड्याच्या लॉजिकप्रमाणे) अशी परिस्थिती पृथ्वीतलावर केवळ उत्तर ध्रुवावर उद्भवू शकते. आणि, उत्तर ध्रुवाजवळची अस्वले पांढरी असतात.
अर्थात, हे लॉजिक पूर्णपणे बरोबर नाही. कारण, (कोणीतरी सुचविल्याप्रमाणे) दक्षिण गोलार्धात असे अगणित बिंदू असू शकतात. दक्षिण ध्रुवाच्या बऱ्यापैकी जवळ, बरोबर एक मैल परीघ असलेले अक्षवृत्त घ्या. (या ठिकाणी, अक्षवृत्ताला वर्तुळाकृती मानले आहे, नि त्याचा 'परीघ' अशी काही संकल्पना गृहीत धरलेली आहे, ती अर्थातच गोलपृष्ठीय भूमितीस अनुसरून नव्हे.) त्यावरील कोणत्याही रँडम बिंदूच्या उत्तरेस एक मैल जा, आणि जेथे पोहोचाल, तेथून शिकारी शिकारीच्या शोधात निघाला, असे माना. मात्र अडचण अशी आहे, की दक्षिण ध्रुवाच्या जवळपास अस्वले नसावीत. त्यामुळे, आपल्या शिकाऱ्यास पेंग्विन टिपावा लागेल. And that would be a dead giveaway, wouldn't it be?
६. तसेही, (उत्तर ध्रुवावर सगळ्याच दिशा दक्षिण असतात, नि दक्षिण ध्रुवावर 'मी म्हणेन ती उत्तर' अशी परिस्थिती असते, या अतिऑबव्हियस अतिबेसिक बाबी तूर्तास बाजूला ठेवून) परंपरेने आपल्या ज्या काही 'उत्तरेकडे तोंड करून उजव्या हाताकडची दिशा ती पूर्व, नि डाव्या हाताकडची दिशा ती पश्चिम' वगैरे पूर्वपश्चिमेच्या व्याख्या - ठोकताळे म्हणा हवे तर - असतात, त्यांची ध्रुवांजवळ पार वाट लागत असेल, नाही? कारण, तेथे रेखावृत्ते ही तरीही दक्षिणोत्तरच जाणार; मात्र, अक्षवृत्ते ही त्या ठिकाणी रेखावृत्तांशी काटकोनात (गोलपृष्ठीय भूमितीत याचा जो काही अर्थ होत असेल, तो - मुळात, एक 'सरळ रेषा' आणि एक 'वक्राकृती' यांच्यातील 'कोन' कसा मोजावा?) नसणार. (हे म्हणणे बरोबर आहे काय? गोलपृष्ठीय भूमितीच्या दृष्टीने सदर रेखावृत्तास 'काटकोना'त छेदणारी जी 'रेषा' (ग्रेट सर्कल) असेल, ती 'अक्षवृत्त' नसणार. उलटपक्षी, त्या ठिकाणी अक्षवृत्त ही मुळात 'रेषा' नसल्यामुळे 'काटकोन' ही कल्पना तेथे बहुधा निरर्थक ठरणार. 'अक्षवृत्ताची (वक्राकृतीची) स्थानिक स्पर्शिका' अशी जरी काही संकल्पना तेथे ओढूनताणून घुसडली, तरी ती स्पर्शिका आणि ते रेखावृत्त यांचे नाते (त्या ठिकाणी) काटकोनाचे नसणार. हे ठीक आहे काय?) उलटपक्षी, (पूर्वपश्चिमेबद्दल) 'उत्तरेकडे तोंड करून डावी-उजवी' या ठोकताळ्यामध्ये 'उत्तरेशी काटकोनात' हे अभिप्रेत आहे. मग आपल्या शिकाऱ्याने एक मैल पूर्वेकडे जे जायचे, ते अक्षवृत्ताचा मागोवा घेत, की हाताच्या आडाख्याने? (मुळात, ध्रुवांच्या अगदी जवळ bearing eastचा अर्थ नक्की काय?)
('सूर्य उगवतो, ती दिशा पूर्व, आणि मावळतो, ती दिशा पश्चिम' हा आडाखा तर त्या भागांत पूर्णपणे गैरलागू असणार. त्यामुळे, तोही उपयोगाचा नाही.)
७. (बरेचसे अवांतर.) पृथ्वीच्या अतिउत्तरेकडील भागांत (उत्तर ध्रुवाजवळ, किंवा अलास्काच्या उत्तरेकडील भागांत वगैरे) जीपीएस प्रणाली गंडते/निकामी ठरते, असे ऐकून आहे. त्यामागील कारण काय असावे? (बहुधा दक्षिण ध्रुवाजवळ तथा अंटार्क्टिकातसुद्धा हे होत असावे, असे वाटते, परंतु कल्पना/खात्री नाही.)
(त्या भागांत होकायंत्रसुद्धा (पृथ्वीचे अक्षीय ध्रुव आणि चुंबकीय ध्रुव यांच्या स्थानांतील फेरफार दुर्लक्षूनसुद्धा) गंडत असणार, हे उघड आहे.)
----------
असो इतकेच. ('For the greatest fool may ask more than the wisest man can answer.') इत्यलम्|
क्र. ४ बद्दल
पृथ्वीवरील कोणत्याहि दोन बिंदूमधील सर्वात कमी अंतर हे 'Great Circle' वर असते. त्या दोन बिंदूंवरील 'Great Circle' म्हण्जे ते दोन बिंदू आणि पृथ्वीचा मध्य ह्यामधून जाणाऱ्या ह्या समतलामुळे पृथ्वीच्या पृष्ठभागावर निर्माण झालेले वर्तुळ. दोन गावांमध्ये येजा करणारी विमाने शक्य तितके अशा 'Great Circle' मार्गाला धरून असतात
समांतर
आपल्या क्रमांक ३ मधील शंकेविषयी: गोलीय पृष्ठभागावरील कुठल्याही दोन सरळ रेषा समांतर असू शकत नाहीत. कारण इथे सरळ रेषा म्हणजे गोलाच्या केंद्रबिंदूतून जाणारे कुठलेही प्रतल (plane) आणि गोलीय पृष्ठभाग ह्यांचे छेदन (intersection)-ह्यालाच great circle (महान वर्तुळ?) असे म्हणतात.
हम्म्म्म्... बहुधा.
म्हणजे, नक्की distinction काय? अक्षवृत्त/रेखावृत्त म्हणजे latitude/longitude (प्रत्यक्ष वृत्ते), तर अक्षांश/रेखांश म्हणजे degree of latitude/longitude (वृत्तांचे कोनीय मोजमाप), असे काही? तसे असल्यास, होय, मला अक्षवृत्त/रेखावृत्त असेच म्हणायचे होते. (My bad!) धन्यवाद.
(ता.क.: बदल केलेला आहे. तसेच, एके ठिकाणी deadly giveaway असा शब्दप्रयोग (चुकून) केलेला होता, तो प्रतिसाद पुन्हा वाचताना माझा मलाच लक्षात आला; तेथेही योग्य ती दुरुस्ती केलेली आहे. पुनश्च आभार.)
RSA Theorem
गूढलेखन (Cryptography) या क्रियेत आपण पाठवलेला संदेश ज्याच्यासाठी आहे त्यालाच समजावा, इतर कुणाला समजू नये याची खबरदारी घ्यावी लागते. आपण दोन मोठ्या मूळ संख्या मनाशी बाळगू आणि ज्याला संदेश पाठवायचा आहे त्याला त्या सांगून ठेवू. या मूळ संख्यांचा गुणाकार करून जी अवाढव्य संख्या मिळेल, तीच फक्त सांकेतिक (coded) संदेश पाठवताना वापरायची. ही अवाढव्य संख्या इतरांना कळली तरी हरकत नाही, कारण संदेशातील संकेत समजण्यासाठी (decoding) आपण घेतलेल्या मूळ संख्या माहित असणे जरूर असते व त्या इतर कुणाला शोधून काढणे अशक्य कोटीतले असते. म्हणून आपला संदेश केवळ इच्छित माणसालाच समजू शकतो. उदाहरणार्थ, 193,707,721 आणि 761,838,257,287 या मूळ संख्यांचा गुणाकार करणे तसे सोपे आहे, निदान संगणकाला तरी; तो गुणाकार आहे 267 – 1. आता 267 – 1 या अवाढव्य संख्येला फक्त वरील दोनच मूळ अवयव आहेत, व नुसती 147,573,952,589,676,412,927 ही 21 आकड्यांची संख्या बघून ते अवयव शोधून काढण्याची संगणकालाही सोपे नाही. म्हणून आपला संदेश आपण ज्याला ते मूळ अवयव आधीच सांगून ठेवले असतील त्यालाच समजू शकतो.
ह्या संकल्पनेला RSA Theorem असे नाव आहे. Ron Rivest, Adi Shamir and Leonard Adleman ह्या तीन संशोधकांच्या MIT मधील सहकार्यातून तिचा उगम झाला आणि त्यांच्या आद्याक्षरावरून तिला RSA Theorem असे नाव मिळाले . MIT ला ह्याचे पेटंटहि मिळाले. पहा: https://en.wikipedia.org/wiki/RSA_(cryptosystem).
शंका?
हे वाक्य मला नीटसं समजलं नाही. दोन सापेक्ष वेग म्हणजे काय हे मला माहीत आहे. -
... दोन सापेक्ष वेगांचे संघटन फार सोप्या प्रकारे करता येते,
या लेखात जे मोठे आकडे आले आहेत - २६७ - १, आणि असे अनेक, ते संगणक वापरून शोधण्यासाठी काही विशेष अल्गोरिदम वापरलं जातं, का निव्वळ संगणकीय शक्ती वापरून एकामागोमागे एक ट्रायल अँड एरर छापानं शोधतात?
मराठी शब्दाबद्दल -
शिवाय त्याने ‘समांतरतेचा कोन’ (Angle of Parallelism) ही संकल्पना प्रस्तुत केली.
ही संकल्पना मांडली, असं म्हणतात त्यापेक्षा काही निराळा अर्थ अपेक्षित आहे का?
शंकानिरसन?
सापेक्ष वेगांचे संघटन: मला भौतिकी मधील फारसे गम्य नाही. पण, ... www.arkiv.org वर J.F. Barrett यांचे The Hyperbolic Theory of Special Relativity या नावाचे पुस्तक उपलब्ध आहे. ते पाहिल्यास काही गोष्टी समजू शकतील. हे उद्धरण पहा: `His (Varicak's) basic result is that the relativistic law of composition of velocities can be interpreted as the triangle of velocities in hyperbolic space and so the kinematic space of Special Relativity is hyperbolic. This view leads to the redefinition of velocity as a hyperbolic velocity more appropriate to relativity.' या बाबतीत `rapidity' (defined in terms of velocity) ही संकल्पना उपयोगी पडते. या पुस्तकाखेरीज, en.wikisource.org वर `Application of Lobachevskian Geometry to the Theory of Relativity' व `The Theory of Relativity and Lobachevskian Geometry' ही व्हारिचाकने १९१० साली लिहिलेल्या दोन शोधनिबंधांची भाषांतरे मिळू शकतात.
अल्गोरिदम: जयदीप चिपलकट्टी यांनी खुलासा केला आहे.
समांतरतेचा कोन: होय, `प्रस्तुत केली' म्हणजे `मांडली' असेच म्हणायचे होते.
> या लेखात जे मोठे आकडे आले
> या लेखात जे मोठे आकडे आले आहेत ... ते संगणक वापरून शोधण्यासाठी काही विशेष अल्गोरिदम वापरलं जातं, का निव्वळ संगणकीय शक्ती वापरून एकामागोमागे एक ट्रायल अँड एरर छापानं शोधतात?
हा विषय भयंकर किचकट आहे. मूळ संख्या शोधणे, दिलेली संख्या मूळ आहे का हे तपासणे, नसेल तर तिचे विभाजक शोधून काढणे यासाठी अनेक अल्गोरिथम्स आहेत आणि त्यांच्यात सुधारणा कशी करायची (म्हणजे वेळ आणि संगणकस्मृती यांची बचत कशी करायची) यावर पेपरामागून पेपर प्रसिद्ध होत असतात. एकूण ह्या अल्गोरिथम्समध्ये घड्याळी अंकगणित (modular arithmetic) + त्यावर आधारित प्रमेयं + ट्रायल अँड एरर यांचं मिश्रण असतं असं मोघमपणे म्हणता येईल. शिवाय elliptic curve नावाची अंकगणित आणि भूमिती अशा दोन्ही प्रांतात पाय रोवून असणारी एक वस्तू असते तीही वापरतात.
हो.संगणक हा स्वतंत्र बुद्धिने काम करत नसतो.
Intuition (?मराठीत) नसते. अगोदर काय झालं आहे म्हणजे तुमच्या डिवाईस हिस्ट्रीत आणि जालावर यातून शोधतो.
साधी साधी गणितं पण अगणित असंख्य प्रमाणात करणे करतो.
मूळ संख्या तपासण्यासाठी २,३,४,५,...न, .न+१ हा अगदी सरधोपट मार्ग. पण शॉर्टकट्स आहेत. पण संख्या मोठी झाली की हेसुद्धा अजमावणे वेळखाऊच होते.
George Gamow - One Two Three...Infinity
ह्या मलिकेतील बहुतेक विषयांना George Gamow ह्यांच्या 'One Two Three...Infinity' नावाच्या पुस्तकामध्ये स्पर्श केला गेला आहे. १९५७-५८ मध्ये मी कॉलेजच्या पहिल्या-दुसऱ्या वर्षामध्ये असतांना हे पुस्तक विद्यार्थ्यांच्यामध्ये बरेच वाखाणले जात असे आणि त्यामुळेच त्या वेळी मी ते वाचलेले होते. ह्या पुस्तकाचा दुसरा भाग 'Space, Time and Einstein' हा विशेषच रंजक होता असे आठवते. आइन्स्टाइनच्या General Theory of Relativity च्या मुळाशी असलेल्या Reimannian Geometry चीहि तोंडओळख ह्या पुस्तकामध्ये झाली. हे पुस्तक archive.org ह्या संस्थळावर येथे उपलब्ध आहे.
"The Birth and Death of the Sun" असे ह्याच लेखकाचे पुस्तकहि वाचनात आले होते.
माणिक टेंबे यांचा अभिप्राय
लिमयेसरांच्या लेखातली त्यांच्या मुलीने दिलेल्या उत्तराची आठवण खूप सुंदर आहे. योग्य प्रकारे जिज्ञासा जागी करून दिली तर मुले किती सुंदर विचार करू शकतात याचे अतिशय मनोज्ञ उदाहरण आहे ही आठवण.
या लेखात अयुक्लीडीय भूमिती आणि मूळ संख्यांबद्दलचे विवेचनही गोष्टीइतके सुरस मांडले आहे. शालेयअभ्यासक्रमातील पाय्, अनंत, पायथॅगोरसचे प्रमेय आणि त्याचे व्यापकीकरण, युक्लीडच्या पाचव्या गृहितकाची गोष्ट, मूळ संख्या या सर्वच संकल्पनांचा स्वतःचा असा सुरस इतिहास आहे आणि तो शाळा कॉलेजातील मुलांपर्यंत पोचला तर त्यांची गणिताची आवड दृढ होईल. शिकवणे अधिक रंजक आणि अर्थपूर्ण होईल.
गणित विषयाबद्दलची आणि एक अडचण म्हणजे गणितात शाळेनंतर पुढे काय असते, गणित विषय निवडला तर आपण काय शिकू? काय काम करू शकू? गणितात कुठचे संशोधन चालू आहे या प्रश्नांची उत्तरे मुलांना कधीच शाळकरी वयात मिळत नाहीत. त्यामुळे गणितात करिअर करण्याचा विचार करणारे फार थोडेच असतात.
'गणिताच्या निमित्ताने'सारखे लेखन म्हणूनही खूप महत्त्वाचे आहे.
माणिक टेंबे.

>>>आता आपण असे म्हणू शकतो की
>>>आता आपण असे म्हणू शकतो की हे गृहीतक मानले तरी प्रत्यक्षात अशा अनेक समांतर रेषा दिसत तर कुठेच नाहीत. इथेच तर मोठी गोम आहे. प्रत्यक्ष अनुभवाला चिकटून राहिलेच पाहिजे असे बंधन गणितज्ञावर नसते. तो एवढेच सुनिश्चित करतो की आपण मानलेली गृहीतके एकमेकांशी सुसंगत आहेत ना. मग अशा सुसंगत गृहीतकांवर आधारलेली सिध्दांतांची इमारत तो रचतो आणि त्या इमारतीच्या सौंदर्यांत हरखून जातो.
या लेखातली अशी काही वाक्य खूप आवडली.