विज्ञान/तंत्रज्ञान
अंदाज करा - इन्फंंट मॉर्टॅलिटी
Taxonomy upgrade extras
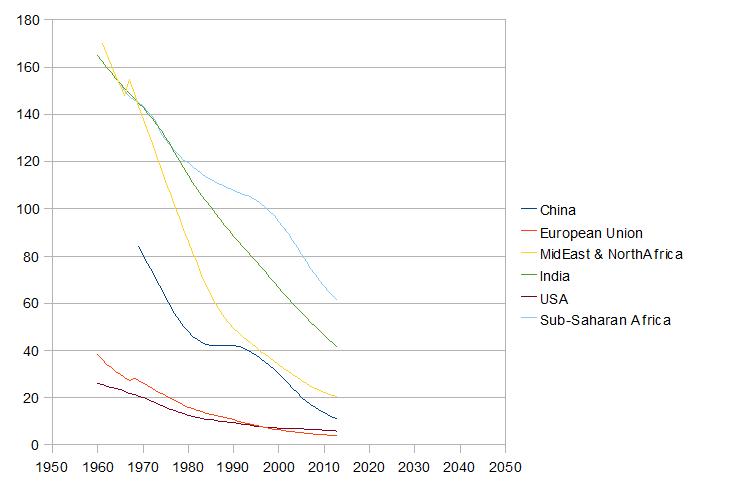
वरील आलेखात गेल्या काही दशकातली इन्फंट मॉर्टॅलिटीची आकडेवारी दिलेली आहे. (इन्फंट मॉर्टॅलिटीने जन्मापासून एका वर्षाच्या आत मृत्यू पावणाऱ्या मुलांचं प्रमाण दर हजार जन्मांमागे दर्शवलं जातं) यात जगाचे पाच मोठे विभाग सामावलेले आहेत.
- Read more about अंदाज करा - इन्फंंट मॉर्टॅलिटी
- 58 comments
- Log in or register to post comments
- 24258 views
हिंदु गणितातील 'वर्गप्रकृति"
Taxonomy upgrade extras
'India gave quadratic equation to world: Rajnath Singh' ह्या बातमीवर 'ही बातंमी समजली का - ५४' ह्या धाग्यामध्ये थोडेसे उपहासाचे प्रतिसाद दिसतात. विमानविद्या आपणच शोधली असले हास्यास्पद शोध जाहीर केल्याने भारताचे हसे होते हे खरे असले तरी ज्या गोष्टी जुन्या काळात आपण खरोखरीच मिळवल्या होत्या त्यांचीहि नोंद केली गेली पाहिजे. वर्गसमीकरणे हा त्याचे एक उदाहरण आहे. त्याविषयी मला असलेली माहिती पुढीलप्रमाणे.
Nx2 + 1 = y2अशा प्रकारच्या समीकरणांना 'वर्गप्रकृति' असे नाव आहे. अशाच प्रकारचे
- Read more about हिंदु गणितातील 'वर्गप्रकृति"
- 38 comments
- Log in or register to post comments
- 18995 views
प्लूटो चा घोळ
Taxonomy upgrade extras
अगदी 21व्या शतकात देखील वैज्ञानिक अन शास्त्रज्ञांची गणिते अन कयासदेखील चुकू शकतात हे सिद्ध झाले . 7/8 वर्षापूर्वी प्लूटो या ग्रहाचा सूर्यमालिकेतील ग्रहाचा दर्जा रद्द करण्यात आला होता, त्यानुसार जगभरातील भूगोलाच्या पाठ्यपुस्तकातून प्लूटो संबंधी माहिती वगळण्यात देखील आली, आणि कालच पुन्हा एकदा तो ग्रह असल्याचे सिद्ध झाले. आता मधल्या काळात चुकीचे विज्ञान शिकवले गेले त्याला जबाबदार कोण ?
- Read more about प्लूटो चा घोळ
- 38 comments
- Log in or register to post comments
- 17036 views
विज्ञान परिषदेत जुन्या विमानांचा विषय
Taxonomy upgrade extras
अरेरे.. का तो जुन्या विमानांचा विषय काढला.. आता तर विज्ञान परिषदेतही मांडला.
:(
भळभळा वाहायला लागतो हो नळ आमचा लगेच.. टाळा ते. :(
(व्यवस्थापन : चर्चा लांबल्यामुळे मूळ धाग्यातून वेगळी काढली आहे.)
- Read more about विज्ञान परिषदेत जुन्या विमानांचा विषय
- 209 comments
- Log in or register to post comments
- 50891 views
एअर-एशिया QZ8501 ... पहाटेचा काळोख...
Taxonomy upgrade extras
शेवटी विमानाचे थोडेसे तुकडे आणि चाळीसेक मृतदेह मिळाल्याचा अपडेट आला. आत्ता तीस डिसेंबरचे पावणेचार (भारतीय वेळ) वाजलेत. आता तासातासाला नवेनवे आकडे येतील आणि नवी वाईट माहितीसुद्धा. MH370 सारखी भयानक अनिश्चितता या विमानाच्या वाट्याला आली नाही, पण हे काही भाग्य म्हणता येत नाही. गडद काळ्याच्या कसल्या शेड्स बघायच्या ?
- Read more about एअर-एशिया QZ8501 ... पहाटेचा काळोख...
- Log in or register to post comments
- 13258 views
मंगलयान...दंगलगान
Taxonomy upgrade extras
फ़क्त 450 कोटी मध्ये मंगळमोहिम आखली गेली...खरच प्रशंसनीय आणि उल्लेखनीय !!
दहा महिन्यापूर्वी पाठवण्यात आलेले 'MOM' नावाचे हे 'अवकाश यान' मंगळाच्या कक्षेत प्रवेश करून निर्विध्नपणे स्थिरावले आणि ही मोहिम यशस्वी झाल्याची सुवार्ता जिकडे तिकडे पसरली आणि मनोमनी इस्त्रोच्या शास्त्रज्ञांचे या कौतुकास्पद कामगिरी बद्दल आभार मानले.
पण...फक्त 450 कोटि मंगळ मोहिमेला वापरले गेले हे कळल्यावर माझ्या डोळ्यापुढे भारतातल्या करोडो रुपयांचे घोटाळ्यांचे आकडे आठवले....बाप रे..!! आणि हा खर्च क्षुल्लक वाटू लागला...
कलमाड़ी फेम कॉमन वेल्थ गेम घोटाळा...8000 करोड़
सारडा चिट फण्ड घोटाळा....5500 करोड़
- Read more about मंगलयान...दंगलगान
- 3 comments
- Log in or register to post comments
- 2363 views
सेंट पीटर्सबर्ग पॅरॅडॉक्स
Taxonomy upgrade extras
उदय यांच्या लेखात 'सेंट पीटर्सबर्ग पॅरॅडॉक्स' चा उल्लेख आलेला आहे, पण त्याचा तपशील दिलेला नाही. तेव्हा वाचकांचा कौल मागवण्यासाठी ही उत्तम संधी आहे. ज्यांना ह्या पॅरॅडॉक्सची उकल ठाऊक आहे त्यांनी ती 'फोडू' नये, आणि ज्यांना त्याची माहिती नाही त्यांनी गूगलगिरी करण्याचा मोह टाळावा ही विनंती.
तर समजा तुम्ही सेंट पीटसबर्गमध्ये झार निकोलसच्या दालनात शिरता.
- Read more about सेंट पीटर्सबर्ग पॅरॅडॉक्स
- 57 comments
- Log in or register to post comments
- 30751 views
Digitization विषयक भारतातील अनास्था.
Taxonomy upgrade extras
माहितगारमराठी ह्यांच्या ’उस्मानियाच्या ऑनलाईन डिजिटल ग्रंथालयात १४०० मराठी पुस्तके’ ह्या http://www.aisiakshare.com/node/3070 येथील धाग्यावरून पुढील लिखाणाचे कारण मला मिळाले. माहितगारमराठी ह्यांच्या लिखाणाचे उद्दिष्ट एक विकीपान निर्माण करणे हे असल्याने पुढील लिखाण आणि त्यावरील चर्चा तेथे अप्रस्तुत ठरेल म्हणून हा वेगळा धागा निर्माण करीत आहे. ह्याचे उद्दिष्ट digitization ची भारतातील दयनीय स्थिति ह्याला आनुषंगिक अशी चर्चा व्हावी हे आहे.
सुमारे दोन वर्षांपूर्वी http://mr.upakram.org/node/3450 असा धागा मी लिहिला होता आणि त्यामध्ये DLI च्या ढिसाळ कारभाराबद्दल आणि तेथे उपलब्ध माहितीच्या अंदाधुंदीबद्दल बरेच काही सोदाहरण लिहिले होते. त्याखालील चर्चेत सर्व प्रतिसाद ह्याला अनुमोदन देणारेच होते.
OUDL DLI हून काकणभर सरस आहे कारण तेथे पीडीएफ फ़ाइल उतरवून घेण्यास मिळते. DLI वाल्यांनी आपल्या संस्थळाच्या वापरात अनेक अडथळे घालून ठेवले आहेत. त्यापैकी एक म्हणजे तेथे पुस्तक उतरवून घेणे वा online वाचणे हे शक्य नाही. त्यासाठी dli downloader ह्या third-party software चा अनधिकृत वापर करावा लागतो.
अजूनहि ती परिस्थिति बदललेली नाही.
मला आश्चर्य असे वाटते की मुंबई-पुणे-नागपूर अशी जुनी विद्यापीठे अणि त्यांची ग्रन्थालये ह्या digitization च्या कामात संपूर्णतया उदास आहेत. अशी विद्यापीठे आणि गावोगावची नगर वाचनालये मिळून हजारो मराठी, संस्कृत आणि अन्य भारतीय भाषांमधील पुस्तके आपल्या कपाटांमधून साठवून आहेत. जसजसा काळ पुढे जात आहे तसतशी ही पुस्तके वाळवी, ओलावा, कागदाचा जुनेपणा, चोर्या, दुर्लक्ष अशा कारणांनी नष्ट होत आहेत. अशा ठेव्याचे रक्षण आणि विस्मृतप्राय अशा ह्या ज्ञानाचा इच्छुकांना वापर करता येईल असे काही करणे हे खरे विद्यापीठे आणि ज्ञानाच्या अन्य क्षेत्रांमधील अन्य संस्था ह्यांचे काम आहे. पण गूगल बुक्स, archive.org,scribd.com अशी संस्थळे अस्तित्वात आल्याला एक दशक लोटत आले तरी इकडे जाग येत नाही असे का? अन्य देशांतील पुष्कळ विद्यापीठे हे कार्य करतात. त्यात भारतीय विद्यापीठे कोठे आहेत?
ह्यापलीकडे मला असाहि प्रश्न पडतो की माहितीचे मोठे खजिने वृत्तपत्रांच्या जुन्या अंकात पडून राहिले आहेत ते digitization मार्गाने विनामूल्य वा थोडे मूल्य घेऊन इच्छुकांना उपलब्ध का करून दिले जात नाही? भारतात टाइंम्सने असा थोडा प्रयत्न केल्याचे दिसते पण तो अतिशय तोटका आणि २००१ सालानंतरचाच आहे. एकाहि मराठी वृत्तपत्राने असे काही केल्याचे मला ठाऊक नाही. वृत्तपत्रांना उत्पन्नाचा हा नवा स्रोत अजून का दिसत नाही? New York Times, London Times, Spectator अशी काही वृत्तपत्रे त्यांच्या पहिल्या दिवसांपासून digitization स्वरूपात उपलब्ध आहेत.
ह्या अनास्थेवर ’ऐसी’च्या वाचकांना काय वाटते?
- Read more about Digitization विषयक भारतातील अनास्था.
- 4 comments
- Log in or register to post comments
- 2669 views
विश्वाची उत्पत्ति - एक 'आस्तिक' विचार
Taxonomy upgrade extras
भूमितीमध्ये आपणास सारख्या भेटणार्या आकृतींमध्ये प्रत्यक्ष निसर्गात नैसर्गिक मार्गाने निर्माण झालेल्या अशा आकृति फार क्वचित दिसतात. शाळेतल्या प्राथमिक भूमितीमध्ये ’सरळ रेषा’ सारखी भेटते, तसेच सरळ रेषा वापरून निर्माण झालेले त्रिकोण, चौरस, पंचकोन हेहि भेटतात. ’वर्तुळ’ ही अशीच एक ubiquitous आकृति. पण ह्या ओळखीच्या आकृति निसर्गात नैसर्गिक मार्गाने निर्माण झालेल्या अशा कोठेच भेटत नाहीत. समोर दिसणारी झाडे, डोंगर-पर्वत, प्राण्यांची शरीरे, फुले-पाने, ढग अशा हजारो गोष्टीमध्ये तुम्हास एकहि नैसर्गिक सरळ रेषा, पूर्ण वर्तुळ दिसणार नाही. सभोवती दिसणार्या सरळ रेषा, पूर्ण वर्तुळे ही मानवनिर्मित घरे, गाडीची चाके अशा वस्तूंमध्येच काय ती दिसतात. Two-dimensional Co-ordinate Geometry मध्ये रेषेचे समीकरण ax+by+c=0, वर्तुळाचे समीकरण x2+y2=1 अशी समीकरणे अगदी सुटसुटीत, ज्यांना elegant म्हणता येईल, अशा प्रकारची असतात पण समोरच्या ढगाच्या चित्राला किंवा फुलाच्या outline ला अशा सुटसुटीत elegant समीकरणामध्ये पकडायचा प्रयत्न करून पहा, तसे करणे अशक्य आहे असे जाणवेल.
एकमेकांशी संबंध नसलेल्या दोन संकल्पनांना एकमेकांशी जुळवायचा प्रयत्न करून पहा. उदाहरणार्थ पृथ्वीला सूर्याभोवती एक पूर्ण प्रदक्षिणा करण्यासाठी लागणारा काळ मोजा आणि पृथ्वीला स्वत:भोवती एक प्रदक्षिणा करण्यासाठी लागणारा काळ मोजा. हे दोन काळ एकमेकांपासून स्वतन्त्र आहेत आणि त्यामुळे त्यांच्यामध्ये सहज मोजण्याजोगा संबंध नाही. रोजच्या व्यवहाराला आवश्यक अशा कालगणनेची निर्मिति तर करायलाच हवी. त्यासाठी असा संबंध जोडण्याचा प्रयत्न म्हणजे कॅलेंडर. ह्या दोघांमध्ये कोणताच सुसूत्रपणा नसल्यामुळे प्राचीन काळापासून कॅलेंडरकर्त्यांना वर्षांमधून काही दिवस वगळणे, वर्षांना काही दिवस तात्पुरते चिकटविणे, leap year अशा कसरती कराव्या लागल्या आहेत आणि ह्यापुढेहि कराव्या लागतील.
पण आइन्स्टाइनचे E=mc2 हे वस्तुमान आणि वस्तुमान आणि वैश्विक शक्ति (जड विश्व आणि चैतन्य) ह्यांमधील संबंध दाखविणारे प्रसिद्ध समीकरण मात्र ह्याला अपवाद आहे, यद्यपि समीकरणातील तिन्ही संज्ञांच्या व्याख्या एकमेकांपासून अनवलम्बित अशा स्वतन्त्र आहेत. निसर्गाच्या एरवी दिसणार्या सवयीनुसार त्यांच्यामधले समीकरण फार गुंतागुंतीचे असायला हवे पण ते तर अगदी सोपे - elegant - आहे. हे का घडले असावे?
ह्या सोपेपणामुळे हे समीकरण कोणा ’नियन्त्या’ने आपल्या ’इच्छे’तून निर्माण केले आहे असा तर्क कोणा आस्तिकाने मांडला तर तो चुकीचा आहे असे म्हणता येईल काय?
(अरुण जोशींच्या ह्या धाग्यावरून माझ्या मनात आलेले हे विचार वेगळ्या दिशेने जातात असे वाटल्यावरून हा धागा निर्माण केला आहे.)
- Read more about विश्वाची उत्पत्ति - एक 'आस्तिक' विचार
- 32 comments
- Log in or register to post comments
- 8834 views
इंटरनेट कनेक्शन - भाग १
Taxonomy upgrade extras
"उपकार?"
"हां हां उपकार."
"वो कैसे?"
"हम आपको टेलिफोन देकर आपकी सेवा ही तो करते है."
"तो सेवा बोलिए ना. ए उपकार कहां से आ गया?"
"जोशीजी, हम आपकी सेवा करते है ये आखिर आप पर उपकार ही तो हुआ ना?"
"तो अब क्या सोची है? उपकार करना बंद करोगे?"
"अरे नहीं बाबू, धीरज रखो."
"वो तो मैं साल से रख रहा हूं. एक तो मै गलती से भी सरकारी कनेक्शन न लेता. लिया है तो केवल अॅड्रेस प्रूफ के लिये. सोचा लिया ही है तो इसी पे ब्रोडबँड भी लेते है. पण आपका फोन ५०% टाइम डाउन होता है. फिर २५% टाइम नेट डायलही नही होता. और बचे हुए २५% टाइम डी एन एस सर्वर डाउन होता है."
"वो डी एन एस तो पिछे से होता है जी"
- Read more about इंटरनेट कनेक्शन - भाग १
- 13 comments
- Log in or register to post comments
- 6376 views
