मला भेटलेले प्राध्यापक श्रीखंडे
मला भेटलेले प्राध्यापक श्रीखंडे
बालमोहन लिमये
(आंतरराष्ट्रीय ख्यातीचे गणितज्ञ प्राध्यापक शरद्चंद्र शंकर श्रीखंडे यांचा सहवास व स्नेह बालमोहन लिमये यांना लाभला. काही दिवसांपूर्वीच प्रा. श्रीखंडे यांचा प्रथम स्मृतिदिन होता. त्या निमित्ताने बालमोहन लिमये यांनी सांगितलेल्या त्यांच्या आठवणी आणि त्यांच्या गणितातील कामगिरीचा करून दिलेला अल्प-परिचय.)
मी २००६ साली निवृत्त झाल्यावरही पुढची जवळ जवळ ११ वर्षे आय्. आय्. टी. बॉम्बेच्या गणित विभागाचा क्रियाशील सदस्य होतो. काम पहिल्यासारखेच, पण उपाधी वेगळ्या. कामाचा ताण मात्र कमी होता. माझ्याकडे पीएच्. डी. करणारे विद्यार्थी नव्हते. मी इतर संस्थांमध्ये जाऊन सहजपणे माझ्या आवडत्या विषयांवर व्याख्याने देऊ शकत होतो. अशीच एक संस्था होती आंध्र प्रदेशातील गुंटुर या शहराजवळची विग्यान युनिव्हर्सिटी. २०१२च्या जानेवारी महिन्यात मी तेथे ‘मूळ संख्यांसंबंधीचे काही प्रश्न’ (Some Questions about Prime Numbers) या विषयावर व्याख्यान दिले. मी टिफ्र (TIFR: Tata Institute of Fundamental Research) या संस्थेत काम करत होतो तेव्हापासून तिथला माझा मित्र तरलोक शोरी मला मूळ संख्यांबाबतच्या नवनवीन शोधांची माहिती पुरवत होताच. ती अशावेळी उपयोगी पडे.
पण गुंटूरला जाण्याचा माझा खरा हेतू वेगळाच होता. जवळच्या मंगलागिरी मंडलातील काझा नावाच्या गावी चिन्मयविजय आश्रम आहे. त्या आश्रमात मला जायचे होते. मी पवईजवळील चिन्मयानंद आश्रमाला कधी कधी एक शांत, प्रसन्न जागा म्हणून भेट देत असे. पण इतका खटाटोप करून गुंटूरच्या आश्रमाला भेट द्यायला मी काही भाविक नव्हतो. त्या आश्रमात लहान मुलींचे एक मोठे अनाथालय होते. इमारतींच्या मध्यवर्ती दोन-दोन खोल्यांची पाच सहा निवासस्थाने होती. त्यातल्या एकात रहात होते प्राध्यापक शरद्चंद्र शंकर श्रीखंडे. मला त्यांना भेटायचे होते.
त्यावेळी प्रा. श्रीखंडे ९४ वर्षांचे होते. ते आणि त्यांची २४ तास काळजी वाहणारा भूपेंद्र सिंह असे दोघेच तिथे रहात होते, अगदी निर्जन जागी. सभोवतीचे सगळे जण फक्त तेलुगु भाषा बोलणारे. बाहेरच्या जगाशी संबंध फक्त टेलिफोनद्वारे किंवा इंटरनेटद्वारे. प्रा. श्रीखंडे इथे कसे येऊन पोहोचले? ही कोण असामी होती? मुख्य म्हणजे मी आणि माझी पत्नी निर्मला आम्ही दोघे जवळजवळ एक हजारपेक्षा जास्त किलोमीटर प्रवास करून, जसे धार्मिक लोक लांबच्या धर्मस्थळाला भेट देतात तसे, त्यांना भेटायला का चाललो होतो?
प्रा. श्रीखंड्यांची आणि माझी पहिली भेट झाली होती १९७१ साली - म्हणजे पन्नास वर्षांपूर्वी. त्यावेळी निर्मला मुंबई विद्यापीठातील गणिताच्या प्रगत अध्ययन केंद्रात (Centre of Advanced Studies in Mathematics) वरिष्ठ संशोधन अधिछात्र (Senior Research Fellow) म्हणून काम करत होती, आणि केंद्राचे निदेशक होते प्रा. श्रीखंडे. निर्मला गरोदर होती, पण तिच्या नेमणुकीमध्ये प्रसूति रजेची (maternity leave) सोयच नव्हती. ती प्रा. श्रीखंडे यांना जाऊन भेटली. त्यांनी विद्यापीठ अनुदान आयोगाकडे (University Grants Commission) अर्ज करायला सांगितला, व शिफारस केली. त्याकाळी विद्यापीठाच्या गणित विभागातील विद्यार्थी टिफ्रमध्ये येऊन संशोधन करत. माझे कार्यालय पण तेथेच होते. प्रा. श्रीखंडे काही दुसऱ्या कामासाठी टिफ्रमध्ये आले असताना मुद्दाम निर्मलाला सांगायला आले की तिचा अर्ज मान्य झाला आहे. मग निर्मला त्यांना माझ्या खोलीत घेऊन आली. मी प्रा. श्रीखंडे यांच्याबद्दल खूप ऐकले होते. पण जेव्हा त्यांनी माझ्या खोलीत पाऊल टाकले तेव्हा मी स्तिमितच झालो. त्यांची सहा फुटी, सावकाश हालचाल करणारी देहयष्टी, प्रसन्न मुद्रा आणि खोलवर पाहणारी नजर यांनी मी इतका भारून गेलो की त्यांनी हस्तांदोलन केव्हा केले ते कळलेच नाही. माझी थोडीशी विचारपूस करून ते बाहेर पडायला निघालेही. या अल्प व अनौपचारिक भेटीचा ठसा माझ्यावर कायमचा राहिला.
पुढील २-३ वर्षांत आमची फारशी मुलाखत झाली नसली तरी निर्मलाकरवी त्यांचे माझ्यावर लक्ष होते. त्यांनी एकदा बॉम्बे मॅथेमॅटिकल कलोक्विअमतर्फे माझे एक व्याख्यानही रुइया कॉलेजमध्ये घडवून आणले होते. मीही निर्मलाकडून त्यांच्याबद्दल ऐकत असे. प्रा. श्रीखंडे १९६३ साली मुंबई विद्यापीठात गणित विभागाचे संस्थापक प्रमुख म्हणून काम करू लागले तेव्हा त्यांच्या सहकाऱ्यांमध्ये एक होत्या वासंती भट. पुणे विद्यापीठातून प्रथम क्रमांकाने गणितात एम्.एस्सी. झाल्यावर त्या मुंबईतील टिफ्र या संस्थेत काम करू लागल्या. पण तेथे मिळालेल्या वागणुकीने त्या आपला आत्मविश्वास गमावून बसल्या. त्या मुंबई विद्यापीठात शिकवू लागल्या, तेव्हा आपण वर्गात जाऊन शिकवू शकतो याचे त्यांचे त्यांनाच आश्चर्य वाटे. एके दिवशी भीतभीतच त्या प्रा. श्रीखंडे यांच्या खोलीत गेल्या आणि म्हणाल्या ‘सर, मला मदत कराल का? माझा आत्मविश्वास पूर्ण गेला आहे. पण मी तुम्हाला वचन देते की मी मन लावून अभ्यास करेन. मला पी. एच्. डी.साठी मार्गदर्शन कराल का?’ श्रीखंडे फक्त म्हणाले ‘ठीक आहे.’ पण त्यांनी वासंतीची मनस्थिती पूर्ण ओळखली होती. त्यांनी प्रथम वासंतीला काही पुस्तके आणि शोधनिबंध अभ्यासायला सांगितले. नंतर संशोधनाकरता एक–दोन प्रश्न सुचवले. वासंतीला केव्हाही त्यांच्या खोलीत जाऊन चर्चा करायची परवानगी दिली. जेव्हा जेव्हा वासंती त्यांच्याकडे आपल्या कल्पना घेऊन जाई, तेव्हा ते पूर्ण लक्ष देऊन तिचे म्हणणे ऐकत आणि म्हणत ‘ठीक वाटताहेत तुझ्या कल्पना. आता त्या गोष्टी सिद्ध करून दाखव.’ वासंती चिकाटीने तिची विधाने सिद्ध करे. एखादे विधान चुकीचे निघाले तरी ते तिला वाईट वाटू देत नसत. हळूहळू वासंतीला आत्मविश्वास परत मिळाला. कालांतराने १९७० साली तिचा प्रबंध मुंबई विद्यापीठाने पीएच्. डी.करता मान्य केला. हे सर्व होत असताना प्रा. श्रीखंडे यांनी वासंतीला एक विद्यार्थी म्हणून न वागवता सहकारी म्हणूनच वागवले. पुढे वासंती भट मुंबई विद्यापीठातील जेष्ठ प्राध्यापक बनल्या, गणित विभागाच्या प्रमुखही झाल्या. श्रीखंड्यांनी घातलेला पायंडा त्यांनी चालू ठेवला. एम्.एस्सी. करताना निर्मला वासंती भट यांची विद्यार्थिनी होती. ती जेव्हा मुंबई विद्यापीठात शिकवण्याकरता रुजू झाली, तेव्हा वासंती भट यांनी निर्मलाला कायमच मानाची, एका सहकाऱ्याची, वागणूक दिली. प्रा. श्रीखंड्यांचा सुस्वभाव असा पसरत असे.
मी टिफ्रमध्ये नुसते संशोधन करण्यात फारसा रमत नाही हे समजल्यावर त्यांनी मला मुंबई विद्यापीठाच्या गोव्यातील पणजी येथील पद्व्युत्तर अध्यापन व संशोधन केंद्रात (Centre for Postgraduate Instruction and Research) जाण्याबद्दल सुचवले. एक वेगळा प्रयोग म्हणून मी ते मानलेही. त्यावेळचे गोव्यातील केंद्राचे निदेशक प्रा. डी. बी. वाघ हे गणिताचे प्राध्यापक होते आणि ते श्रीखंड्यांना चांगले ओळखत. नवीन मुलुख आणि नवीन माणसे, आणि मुख्यत्वे विद्यार्थ्यांना शिकवायची संधी यांमुळे आमचे गोव्यातील सुरुवातीचे वास्तव्य सुखकारक झाले. त्या काळात निर्मलाने तिच्या पीएच्. डी.चे संशोधनही पूर्ण केले. पाच-सहा महिन्यांनंतर जरा मोठा आवाका असलेल्या ठिकाणी जावेसे मला वाटू लागले. निर्मलालाही गोव्यांत काम करण्याची फारशी संधी दिसत नव्हती. कांही निमित्ताने मी मुंबईला आलो असताना अचानक मला समजले की २-३ दिवसांत आय्. आय्. टी.च्या गणित विभागात साहाय्यक प्राध्यापकाच्या पदासाठी मुलाखती होणार आहेत. त्या वेळच्या गणित विभागाचे प्रमुख प्रा. मनोहर वर्तक यांना मी भेटलो आणि अर्ज लिहून दिला. सुदैवाने मला मुलाखतीसाठी बोलावण्यात आले. मुलाखत घेणाऱ्या विशेषज्ञांमध्ये होते प्रा. श्रीखंडे, टिफ्रचे प्रा. एम्. एस्. नरसिंहन् आणि दुसरे दोघेजण. माझी मुलाखत चांगली झाली. आय्. आय्. टी.कडून नियुक्तिपत्र खूप उशीरा, म्हणजे एप्रिल १९७५ मध्ये आले, पण दुसऱ्याच दिवशी मला माझी निवड झाल्याचे कळले होते.
आम्ही मुंबईला आल्यावर काही महिन्यांतच निर्मला मुंबई विद्यापीठाच्या गणित विभागात शास्त्रीय संकोष अधिकारी (Scientific Pool Officer) आणि नंतर प्रपाठक (Reader) म्हणून काम करू लागली. ती एम्.एस़्सी. करत असताना तिला प्रा. श्रीखंडे यांनी शिकवले होते. आता ती त्यांची सहकर्मी (colleague) झाली. त्यांच्या विभागात प्रा. श्रीखंडे यांचा दबदबा तर होताच, पण ते इतके साधे व निगर्वी होते की विभागप्रमुखाच्या कार्यालयातील वातावरण अगदी खेळीमेळीचे रहात असे. कुणालाही काही अडचण आली की त्यातून ते मार्ग काढत असत. काही कारणास्तव मी विद्यापीठात गेलो किंवा प्रा. श्रीखंडे आय्. आय्. टी.त आले तर मी त्यांना जरूर भेटत असे. त्यांच्या सान्निध्यात असताना आपण एका अतिशय बुद्धिमान आणि तितक्याच सज्जन माणसाबरोबर असल्याची सतत जाणीव होत असे. ते क्षण जपून ठेवावेत असे वाटे.
आय्. आय्. टी.त माझ्याकडे पी.एच्.डी. करणाऱ्या शरद सानेचा विषय प्रा. श्रीखंडे यांच्या प्रांतातलाच होता. १९७८ मध्ये शरदच्या प्रबंधाचे परीक्षण कराल का, असे मी त्यांना विचारले. पण त्याच वेळी प्रा. श्रीखंडे मुंबई विद्यापीठातून निवृत्त होण्याच्या बेतात होते. त्यांनी टिफ्रमध्ये काम करणारा त्यांचा विद्यार्थी डॉ. नवीन सिंघी याचे नाव सुचवले. प्रा. श्रीखंडे निवृत्त होण्याच्या आधी मुंबई विद्यापीठाच्या गणित विभागातील सर्वजण आपापल्या जोडीदारांसह दक्षिण मुंबईतील ब्रिस्टोल ग्रिल या रेस्टॉरन्टमध्ये जमले होते. आम्हा दोघांबरोबर शरद सानेही आला होता. मुंबईमधील अनेक महाविद्यालयातील प्रा. श्रीखंड्यांचे चाहते आणि टिफ्रमधील प्रा. नरसिंहन्, प्रा. श्रीधरन्, प्रा. बालगंगाधरन् उपस्थित होते. प्रा. श्रीखंडे त्यांच्या नेहमीच्या साध्या सुती कपड्यांतच होते. अनेक जणांनी भाषणे केली. मी मात्र काही बोललो नाही. एकतर मी त्यावेळी खूप कनिष्ठ होतो, आणि दुसरे म्हणजे अशा प्रसंगी प्रा. श्रीखंडे यांच्यासारख्या व्यक्तीसंबंधी बोलताना माझे डोळे पाणावतात.
मुंबई विद्यापीठातून बाहेर पडल्यावर प्रा. श्रीखंडे यांनी अलाहाबाद मधील मेहता संशोधन संस्थेचे (आताच्या हरिश्चंद्र संशोधन संस्थेचे) निदेशकपद स्वीकारले. आपली पत्नी शकुंतला व बौद्धिकदृष्ट्या अक्षम असा मोठा मुलगा विजय यांच्यासह ते तिकडे रवाना झाले. विजय ही त्यांची मर्मबंधातील ठेव होती. त्याच्याबद्दल वाटणारी काळजी ते कधीही चेहऱ्यावर दाखवत नसत. पण त्याची जबाबदारी त्यांनी कधीही आपल्या इतर मुलांवर टाकली नाही, अगदी पत्नी निवर्तल्यावरही. त्यांच्या पत्नीने आपले सर्व आयुष्य नवरा आणि मोठा मुलगा यांना वाहिल्यामुळेच प्रा. श्रीखंडे संशोधनातील काम करू शकले. त्यांची अलाहाबादमधील सुरुवातीची वर्षे बरी गेली, पण नंतर त्यांच्या पत्नीला स्तनाच्या कॅन्सरने पछाडले.
मी १९८७ साली काही महिने कॅनबेरा येथील ऑस्ट्रेलियन नॅशनल युनिव्हर्सिटीत काम करत असताना एक विनिबंध (monograph) लिहिला. तो तेथील Proceedings of Centre for Mathematical Analysis चा एक खंड म्हणून प्रकाशित झाला. भारतात परतल्यावर १९८८ साली मार्च महिन्यात मी त्याची एक प्रत प्रा. श्रीखंडे यांना पाठवली आणि सोबत एक पत्रही लिहिले. तेव्हा प्रा. श्रीखंडे नागपूरला स्थायिक झाले होते. त्यांच्या पत्नीची तब्येत खालावल्यामुळे काळजीत होते. तरीही चार दिवसांत त्यांनी मला उत्तर पाठवले. स्वतःच्या हस्ताक्षरात, एकही शब्द न खोडता, पुरी दोन पाने त्यांनी लिहिली होती. प्रवाही इंग्लिशमधील ते पत्र मी अजून जपून ठेवले आहे. मी लिहिलेला विनिबंध संक्षिप्त रूपात एखाद्या भारतीय संस्थेतर्फे प्रकाशित करता आला तर तो इथल्या विद्यार्थ्यांना परवडेल व उपयोगी ठरेल, असे त्यांनी म्हटले होते. मी माझ्या पत्रात त्यांच्या माझ्यावरील कृपादृष्टीचा उल्लेख करून विचारले होते की मी काही त्यांचा विद्यार्थी किंवा सहकर्मी नव्हतो, त्यांचे आणि माझे संशोधनविषयही वेगळे होते, मग त्यांच्या मनात माझ्याबद्दल मृदुभाव का वसावा. त्यांनी लिहिलेल्या मजकुराचे मराठीत भाषांतर असे करता येईल : ‘तुम्ही मला विचारलेल्या प्रश्नाचे उत्तर सोपे आहे. तुमची गणितातील गति, तुम्हाला गणिताबद्दल वाटणारी तळमळ आणि तुम्हाला मिळणाऱ्या प्रत्येक संधीचा तुम्ही करत असलेला पुरेपूर उपयोग यामुळेच माझ्या मनात तुमच्याबद्दल मृदुभाव आहे. शिवाय त्याचे एक कारण निर्मलाही आहे. (पण तिला त्याचे फार श्रेय घेऊ देऊ नका!)’ हे वाचून मला हुरूप तर आलाच, पण त्यांचे हळूच चिमटा काढण्यातले कसब लक्षात आले. मला कधी कधी वाटे की प्रा. श्रीखंडे यांना निर्मलापेक्षा माझ्याबद्दल जास्त जिव्हाळा होता. अर्थात् निर्मलाला याच्या नेमके उलटे वाटत असे. प्रा. श्रीखंड्यांनी पाठवलेल्या उत्तरावरून त्यांना स्वत:ला गणिताबद्दल व गणितात प्रगती करू पाहणाऱ्या तरुण लोकांबद्दल किती ममता वाटत असे ते कळून चुकते.

प्रा. श्रीखंडे यांनी १५ मार्च १९८८ रोजी मला लिहिलेल्या पत्राचा एक भाग
काही महिन्यांतच सौ. श्रीखंडे यांचे निधन झाल्यावर आम्ही नागपूरला जाऊन प्रा. श्रीखंडे यांना भेटलो होतो. त्यावेळी त्यांच्या तब्येतीवर आपल्या मुलाच्या – विजयच्या – काळजीचा बराच परिणाम झालेला दिसत होता. प्रा. श्रीखंडे यांच्या अमेरिकेत स्थायिक झालेल्या मोहन, आशा आणि अनिल या तीन मुलांनी त्यांना काही महिन्यांकरता अमेरिकेला नेले. थोड्याशा आजारानंतर विजयचा मृत्यू झाला. काळजी ओसरल्याने आणि हवा, स्थळ व माणसे यांच्यातील बदलाने प्रा. श्रीखंडे यांची तब्येत सुधारली. भारतात परतल्यानंतर ते काही काळ नागपूरला आणि काही काळ त्यांच्या जन्मस्थळी मध्यप्रदेशातील सागरला राहिले. मधूनमधून मुलांकडे अमेरिकेला जाताना आणि येताना ते मुंबईला आवर्जून थांबत. त्यांचे मुंबई विद्यापीठातील सहकारी निर्मला, शरद साने आणि प्रफुल्लता चवाथे यांच्याकडे आलटून पालटून मुक्काम करत. आमच्याकडे असताना आमच्या मुली, निर्मलाची आई या सर्वांशी इतके मिळून-मिसळून वागत की कुणाला वाटावे की ते घरातले आजोबाच आहेत. एकदा अमेरिकेहून परत येताना त्यांनी एक भेटवस्तू आणली होती. ती म्हणजे ‘The Man Who Loved Only Numbers’ हे पॉल एर्डिश यांच्या जीवनावरचे पुस्तक, पॉल हॉफमन यांनी लिहिलेले. पहिल्या पानावर ‘निर्मला व बालमोहन यांना, उत्तम शुभेच्छांसह’ असे लिहून सही केली होती. ते पुस्तक आम्ही दोघांनीही रस घेऊन वाचले. आजही ते जपून ठेवले आहे, त्याला ब्राऊन पेपरचे वेष्टन घालून.

तरुणपणीचे प्रा. श्रीखंडे
प्रा. श्रीखंडे यांची शैक्षणिक क्षेत्रातील पार्श्वभूमी, व त्यांचे गणित आणि सांख्यिकी (statistics) या विषयांतील काम याबद्दल थोडेफार लिहिणे वावगे होणार नाही. नागपूरमध्ये बी.एस्सी.पर्यंतचे शिक्षण घेतल्यावर ते कलकत्त्याच्या इंडियन स्टॅटिस्टिकल इन्स्टिट्यूटमध्ये (I. S. I.) पोचले, एक सांख्यिकी विषयातील साहाय्यक (statistical assistant) म्हणून. तिथे त्यांची आणि सांख्यिकीमध्ये ख्यातनाम असलेले राज चंद्र बोस यांची गाठ पडली. नंतर ते प्रा. बोस यांच्याबरोबर पीएच्. डी. करण्याकरता अमेरिकेतील नॉर्थ कॅरोलिना विद्यापीठात दाखल झाले. प्रा. बोस यांच्या स्फूर्तिदायक मार्गदर्शनाखाली त्यांनी एका वर्षात काम पूर्ण केले आणि १९५० साली पी.एच्. डी. ही पदवी मिळवली. परत आल्यावर नागपूरच्या सायन्स कॉलेजमध्ये ते प्राध्यापक म्हणून काम करू लागले.

चॅपेल हिल मधील नॉर्थ कॅरोलिना विद्यापीठाच्या सांख्यिकी विभागात, १९५८
(मध्यभागी बसलेले प्रा. एच्. होटेलिंग, त्यांच्या डावीकडे प्रा. आर्. सी. बोस,
आणि उजवीकडे एस्. एन्. रॉय. अगदी उजवीकडे मागे उभे एस्. एस्. श्रीखंडे)
१९५९ हे वर्ष प्रा. श्रीखंडे यांच्या शास्त्रीय जीवनात फार महत्त्वाचे ठरले. आदल्या वर्षी ते प्रा. बोस यांच्या आमंत्रणावरून अमेरिकेतील नॉर्थ कॅरोलिना विद्यापीठात संशोधन करण्यासाठी गेले होते. तेथे त्यांनी ज्या दोन मोठ्या गोष्टी सिद्ध केल्या, त्यांची नुसती थोरवी गाण्याऐवजी त्या नेमक्या काय होत्या याची कल्पना देण्याचा प्रयत्न करतो. त्यासाठी जरूर असणारे थोडे गणित जाणून घेऊ या. शालेय अभ्यासक्रमात गणित शिकलेल्या व्यक्तीला हा भाग कळायला जड जाऊ नये. त्यानंतर पुन्हा प्रा. श्रीखंडे यांच्या आठवणींकडे वळू.
टिक्-टॅक्-टो या खेळात आपण एक चौरस ३ x ३ लहान चौरसांत विभागतो, तर बुद्धिबळाचा पट ८ x ८ लहान चौरसांत विभागलेला असतो, आणि सुडोकू या खेळात ९ x ९ लहान चौरसांची घरे असतात. त्याचप्रमाणे न ही कोणतीही नैसर्गिक संख्या (natural number) असेल आणि आपण एक चौरस समान आकाराच्या न x न लहान चौरसांत विभागला तर आपल्याला न x न आकाराची जाळी (grid) मिळेल. तिच्यातील प्रत्येक चौरसामध्ये १, २, . . . , न यांपैकी एक आकडा असा लिहायचा की प्रत्येक आडव्या ओळीत १ ते न असे सर्व आकडे असतील, आणि तसेच प्रत्येक उभ्या ओळीतही १ ते न असे सर्व आकडे असतील. या प्रकारची मांडणी असलेल्या चौरसाला न x न आकाराचा लॅटिन चौरस (Latin Square of order n, or of size n x n) असे म्हणतात. जर न = २ घेतले, तर पुढील दोनच लॅटिन चौरस आपल्याला मिळतात :

न = २
जर न = ३ घेतले, तर पुढील तीन आणि असेच आणखी ९ लॅटिन चौरस सहज मिळू शकतात :
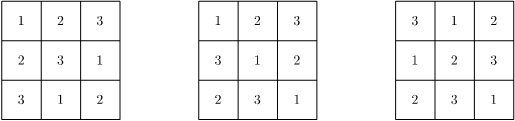
न = ३
आता न ही कुठलीही नैसर्गिक संख्या घेतली तर न x न आकाराचा एक तरी लॅटिन चौरस आपण चटकन् लिहू शकतो. पहिली ओळ १, २, . . ., न, दुसरी ओळ २, ३, . . ., न, १, तिसरी ओळ ३, ४, . . ., न, १, २, असे करत शेवटची ओळ न, १, . . ., न - २, न – १ अशी लिहायची. इथे आपण एकापुढची एक ओळ लिहिताना एकेक नंतरच्या आकड्याने सुरुवात करतो, आणि न पर्यंत पोहोचलो की पुन्हा १ वर येतो.
या पुढे जाऊन न x न आकाराचेच, पण खऱ्या अर्थाने वेगळे, असे दोन तरी लॅटिन चौरस मिळतात का, असा प्रश्न विचारू या. खऱ्या अर्थाने वेगळे म्हणजे असे : समजा दोन न x न आकाराचे लॅटिन चौरस आपण बरोबर एकमेकांवर ठेवले. एकमेकांवर पडलेल्या आकड्यांच्या ज्या न२ जोड्या होतात त्या सगळ्या जर वेगवेगळ्या असल्या, तर ते खऱ्या अर्थाने वेगळे असे समजायचे. उदाहरणार्थ, २ x २ आकाराचे जे दोन लॅटिन चौरस आहेत, ते एकमेकांवर ठेवले तर (१, २), (२, १) अशा दोन जोड्या प्रत्येकी दोन वेळा येतात, आणि म्हणून ते खऱ्या अर्थाने वेगळे नाहीत. आता ३ x ३ आकाराच्या वर दिलेल्या तीन लॅटिन चौरसांपैकी पहिले दोन एकमेकांवर ठेवले तर (१, १), (२, २), (३, ३), (२, ३), (३, १), (१, २), (३, २), (१, ३) आणि (२, १) अशा नऊ वेगवेगळ्या जोड्या मिळतात, आणि म्हणून ते दोन लॅटिन चौरस खऱ्या अर्थाने वेगळे; उलटपक्षी, त्यांपैकी जर पहिला आणि तिसरा हे लॅटिन चौरस एकमेकावर ठेवले तर (१, ३), (२, १) आणि (३, २) या तीन जोड्या प्रत्येकी तीन वेळा येतात, आणि म्हणून ते खऱ्या अर्थाने वेगळे नाहीत.
दोन न x न आकाराचे लॅटिन चौरस खऱ्या अर्थाने वेगळे असणे याला ते एकमेकांशी काटकोनी अथवा लंबकोनी (orthogonal) आहेत असे म्हणतात. ३ x ३ प्रमाणेच, ४ x ४ आकाराचे दोन आणि ५ x ५ आकाराचे दोन काटकोनी लॅटिन चौरस मिळवणे अवघड नाही. उदाहरणार्थ, हे ४ x ४ आकाराचे दोन काटकोनी लॅटिन चौरस आहेत :
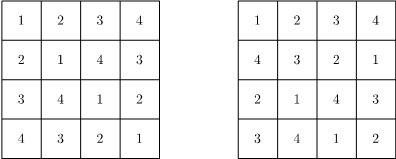
न = ४
तर ५ x ५ आकाराचे दोन काटकोनी लॅटिन चौरस आहेत :

न = ५

लिओनार्ड ऑयलर (१७०७-१७८३)
१७८२ साली लिओनार्ड ऑयलर (Leonhard Euler) हा स्विस गणितज्ञ ६ x ६ आकाराचे दोन काटकोनी लॅटिन चौरस शोधत होता - रशियातील सेंट पीटर्सबर्ग ॲकेडमीमध्ये, तेथील राणी कॅथेरिन् द ग्रेट (Catherine the Great) हिने विचारल्यावरून. तिला सैन्यातील ३६ अधिकाऱ्यांना ६ x ६ आकाराच्या जाळीमध्ये असे उभे करायचे होते की प्रत्येक आडव्या आणि प्रत्येक उभ्या ओळीमध्ये सैन्याच्या ६ तुकड्यांपैकी एकेक आणि ६ हुद्द्यांपैकी एकेक अधिकारी असेल. राणीला हवी असलेली रचना ६ x ६ आकाराचे दोन काटकोनी लॅटिन चौरस मिळवून करता येते. पण खूप प्रयत्न करूनही ऑयलरला असे दोन चौरस सापडले नाहीत. उलटपक्षी, ऑयलरला माहीत होते की न ही कुठलीही १पेक्षा मोठी नैसर्गिक संख्या असेल व तिला ४ने भागल्यावर बाकी जर ०, १ किंवा ३ उरत असेल, तर न x न आकाराचे दोन काटकोनी लॅटिन चौरस जरूर मिळतात. २ x २ आकाराचे दोन काटकोनी लॅटिन चौरस नसतात हे तर उघडच होते, आणि ६ x ६ आकाराचे दोन काटकोनी लॅटिन चौरस तर मिळत नव्हते. ह्या गोष्टींरून त्याने असा अंदाज केला की जर न या नैसर्गिक संख्येला ४ने भागल्यावर बाकी २ उरली (म्हणजे न ही संख्या २, ६, १०, १४, . . . यांपैकी असली), तर न x न आकाराचे दोन काटकोनी लॅटिन चौरस मिळणारच नाहीत. या विधानाला ऑयलरचे अनुमान (Euler’s conjecture) असे म्हणतात.
१२८ वर्षांनी, म्हणजे १९०० साली, गास्तों तारी (Gaston Tarry) या फ्रेंच गणितज्ञाने ऑयलरचे अनुमान न = ६ या संख्येसाठी खरे असल्याचे दाखवून दिले. याकरता त्याने ६ x ६ आकाराचे सगळे लॅटिन चौरस तपासले, व त्यातले कुठलेही दोन एकमेकांशी काटकोनी नाहीत हे पडताळून बघितले. ६ x ६ आकाराच्या लॅटिन चौरसांची संख्या आहे ८१,२८,५१,२००. पण यांपैकी फक्त ९,४०८ चौरस असे आहेत की ज्यांची पहिली आडवी ओळ आणि पहिली उभी ओळ १, २, ३, ४, ५, ६ अशी आहे. याचा उपयोग करून, त्याकाळी संगणक नसले तरी, हे जिकिरीचे काम तारीने पार पाडले. तरीही १०, १४, १८, २२, . . . या संख्यांसाठी ऑयलरचे अनुमान सत्य आहे की असत्य आहे हा प्रश्न तसाच राहिला होता. या प्रश्नावर आर्. सी. बोस व एस्. एस्. श्रीखंडे हे नॉर्थ कॅरोलिना विद्यापीठातील प्राध्यापक, आणि रेमिंग्टन रँड कंपनीच्या युनिव्हॅक विभागातील इ. टी. पार्कर काम करू लागले. प्रथमतः इतरांप्रमाणे त्या तिघांनाही ऑयलरचे अनुमान खरे आहे असेच वाटत होते. परंतु आतापर्यत न वापरलेल्या काही वेगळ्या पद्धतीने ते विचार करत होते. अखेरीस १९५९ सालच्या एप्रिल महिन्यात या तिघांनी अमेरिकन मॅथेमॅटिकल सोसायटीच्या सभेमध्ये जाहीर केले की ऑयलरचे अनुमान न = २ आणि न = ६ या संख्या सोडून उरलेल्या सगळ्या (ज्यांना ४ने भागल्यावर बाकी २ उरते अशा) संख्यांसाठी असत्य आहे. त्यांनी रचनात्मक सिद्धताही दिली. या कामी युग्मतः संतुलित संकल्पना (pairwise balanced designs) महत्त्वपूर्ण ठरल्या. ही फारच खळबळजनक बातमी होती. ऑयलरला सपशेल खोटे ठरवणे ही काही लहानसहान गोष्ट नव्हती. रविवार, तारीख २६ एप्रिलला न्यू यॉर्क टाइम्सच्या पहिल्या पानावर बोस, श्रीखंडे आणि पार्कर यांचा फोटो झळकला.

न्यू यॉर्क टाइम्स, २६ एप्रिल १९५९
या फोटोत पार्कर एक १० x १० आकाराचा लॅटिन चौरस काढताना दिसत आहेत. बरोबरच्या बातमीत लिहिले होते की या तिघांचे सहकारी त्यांना ‘Euler’s Spoilers’, म्हणजे ऑयलरला खोडून काढणारे असे संबोधू लागले आहेत! ऑयलरसारख्या निष्णात गणितज्ञाचेही अंदाज चुकू शकतात तर! न्यू यॉर्कमधील ज्या हॉटेलमध्ये श्रीखंडे रहात होते तेथील एका कर्मचाऱ्याने ‘त्या फोटोमध्ये तुम्हीच आहात का?’ असे श्रीखंड्यांना विचारले. त्यांनी होकारार्थी मान डोलावली तेव्हा तो म्हणाला, ‘तुम्ही खरेच काही तरी अजब केले असले पाहिजे, कारण न्यू यॉर्क टाइम्सचे पहिले पान लाखो डॉलर्स देऊनही विकत घेता येत नाही.’ पुढल्या वर्षी ‘कॅनेडियन जर्नल ऑफ् मॅथेमॅटिक्स’मध्ये बोस, श्रीखंडे आणि पार्कर यांचा याविषयीचा शोधनिबंध प्रसिद्ध झाला, आणि एका उच्च प्रतीच्या कामावर शिक्कामोर्तब झाले.
याच सुमारास प्रा. श्रीखंडे यांनी लावलेला आणखी एक महत्त्वाचा शोध ‘ॲनल्स ऑफ मॅथेमॅटिकल स्टॅटिस्टिक्स' या संशोधनपत्रिकेत प्रसिद्ध झाला. त्याचे वर्णन करण्यासाठी काही पूर्वतयारी करू या. या भागाच्या आकलनासाठीही शालेय अभ्यासक्रमातील गणित पुरेसे आहे. शेवटच्या भागात प्रा. श्रीखंडे यांच्या आणखी आठवणी सांगणार आहे.
समजा एका कागदावर आपण काही बिंदू काढले आहेत. त्यांपैकी कोणते दोन बिंदू एकमेकांना जोडायचे आणि कोणते दोन बिंदू नाही जोडायचे ते आपणच ठरवायचे, आणि ठरवल्याप्रमाणे (सरळ किंवा वक्र) रेषा काढून ते बिंदू एकमेकांना जोडून टाकायचे. या रेषा एकमेकींना छेदू शकतात; फक्त कुठले दोन बिंदू कुठल्या रेषेने जोडले जात आहेत ते नीट कळले पाहिजे, इतकेच. अशा प्रकारे जे चित्र काढले जाते त्याला गणिताच्या समचय (Combinatorics) या शाखेत आलेख (graph) असे नाव आहे. जे दोन बिंदू एकमेकांना जोडलेले असतात त्यांना एक-दुसऱ्याचे शेजारी (neighbours) किंवा लगतचे (adjacent) असे म्हणतात. उदाहरणार्थ, कागदावर खालीलप्रमाणे असे १६ बिंदू काढू या :
(१, ३), (२, ३), (३, ३), (४, ३)
(१, २), (२, २), (३, २), (४, २)
(१, १), (२, १), (३, १), (४, १)
यांपैकी कोणतेही दोन बिंदू जर आडव्या सरळ ओळीत किंवा उभ्या सरळ ओळीत असले तरच त्यांना एका रेषेने जोडायचे असे ठरवू या; ही रेषा सोयीप्रमाणे सरळ किंवा वक्र असू शकते. मग असा आलेख काढता येतो :
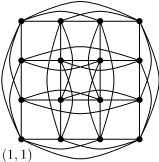
वरील चित्रावरून या आलेखाचे पुढील गुणधर्म दिसून येतात :
- एकूण बिंदूंची संख्या १६ आहे.
- प्रत्येक बिंदू ६ बिंदूंना जोडला आहे.
- कोणतेही दोन बिंदू घेतले, मग ते एकमेकांचे शेजारी असोत किंवा नसोत, तर त्या दोन्ही बिंदूंना जोडले जाणारे इतर २ बिंदू आहेत.
श्रीखंडे यांनी हेच तीन गुणधर्म असणारा पण एक भिन्न आलेख काढला, कोणते दोन बिंदू एकमेकांशी जोडायचे ते वेगळ्या प्रकारे ठरवून. तो श्रीखंडे आलेख (Shrikhande graph) या नावाने ओळखला जातो.
आधीच्या आलेखात वर दिलेल्या १६ बिंदूंपैकी (अ, ब) आणि (क, ड) हे दोन बिंदू एकमेकांचे शेजारी असतात याचा अर्थ अ = क किंवा ब = ड असा होतो. उलटपक्षी, श्रीखंडे यांनी ठरवले की त्यांच्या आलेखात वरील १६ बिंदूंपैकी (अ, ब) आणि (क, ड) हे दोन बिंदू एकमेकांचे शेजारी असतात याचा अर्थ पुढील सहा अटींपैकी एक अट पुरी होते असा करायचा :
- अ = क आणि ब = ड + १,
- अ = क आणि ब + १ = ड,
- अ = क + १ आणि ब = ड,
- अ = क + १ आणि ब = ड + १,
- अ + १ = क आणि ब = ड,
- अ + १ = क आणि ब + १ = ड.
या अटी लिहिताना ४ + १ = १ असे मानले आहे.
आधीच्या आलेखात (१, १) या बिंदूचे शेजारी आहेत (२, १), (३, १), (४, १), (१, २), (१, ३) व (१, ४), आणि हे शेजारी एकमेकांत ३ लांबीची दोन चक्रे (cycles) बनवतात, एक चक्र (२, १) → (३, १) → (४, १) → (२, १) असे, व दुसरे चक्र (१, २) → (१, ३) → (१, ४) → (१, २) असे. श्रीखंडे आलेखात त्यांनी ठरवलेल्या वेगळ्या ‘शेजारधर्मा’प्रमाणे (१, १) या बिंदूचे शेजारी आहेत (२, १), (१, ४), (४, ४), (४, १), (१, २) व (२, २), आणि हे शेजारी एकमेकांत ६ लांबीचे एक चक्र (cycle) बनवतात, (२, १) → (१, ४) → (४, ४) → (४, १) → (१, २) → (२, २) → (२, १) असे. यामुळे हे दोन आलेख भिन्न आहेत हे सिद्ध होते. खालील चित्रात या दोन आलेखांतील (१, १) हा बिंदू त्याच्या शेजाऱ्यांना काळ्या रंगाच्या रेषांनी जोडून दाखवला आहे, आणि हे शेजारी एकमेकांना कसे जोडले जातात ते लाल रंगाच्या रेषांनी दाखवले आहे. डावीकडची आकृती आधी वर्णन केलेल्या आलेखाचा एक भाग आहे, आणि उजवीकडची आकृति श्रीखंडे आलेखाचा एक भाग आहे.

हे दोन आलेख भिन्न आहेत हे खरे. पण कोणी या दोन्ही आलेखांपेक्षाही भिन्न आलेख काढू शकेल का? श्रीखंडे यांनी गणिती युक्तिवादाने सिध्द केले की आधी निर्देशिलेले तीन गुणधर्म बाळगणाऱ्या ह्या दोन आलेखांपेक्षा भिन्न असा आलेख असूच शकत नाही. ही मोठी गोष्ट होती.
आता म ही कोणतीही १ पेक्षा मोठी नैसर्गिक संख्या (natural number) घेऊ या. एका कागदावर खालीलप्रमाणे म२ बिंदू काढू या :
(१, म-१), (२, म-१), ..., ..., ..., (म, म-१)
. . . . . .
. . . . . .
(१, २), (२, २), ..., ..., ..., ..., (म, २)
(१, १), (२, १), ..., ..., ..., ..., ..., (म, १)
आधीप्रमाणेच कोणतेही दोन बिंदू जर आडव्या सरळ ओळीत किंवा उभ्या सरळ ओळीत असले तरच त्यांना (सरळ किंवा वक्र) रेषेने जोडायचे. याही आलेखात वर दिलेल्या म२ बिंदूंपैकी (अ, ब) आणि (क, ड) हे दोन बिंदू एकमेकांचे शेजारी असतात याचा अर्थ अ = क किंवा ब = ड असा होतो.
याप्रमाणे काढलेल्या आलेखाचे गुणधर्म पुढीलप्रमाणे आहेत :
- एकूण बिंदूंची संख्या म२ आहे.
- प्रत्येक बिंदू २(म - १) बिंदूंना जोडला जातो. (त्या बिंदूच्या आडव्या ओळीतील म – १ बिंदू आणि उभ्या ओळीतील म – १ बिंदू)
- कोणतेही दोन बिंदू एकमेकांचे शेजारी असले, तर त्या दोन्ही बिंदूंना जोडले जाणारे इतर म - २ बिंदू असतात. (ते दोन बिंदू सोडून आडव्या किंवा उभ्या ओळीतील उरलेले म - २ बिंदू)
- कोणतेही दोन बिंदू एकमेकांचे शेजारी नसले, तर त्या दोन्ही बिंदूंना जोडले जाणारे इतर २ बिंदू असतात. (त्या दोन बिंदूंतून जाणाऱ्या दोन आडव्या रेषा आणि दोन उभ्या रेषा एकमेकींना आणखी जेथे छेदतात ते २ बिंदू)
उदाहरणार्थ, जर म = २ असेल, तर हा आलेख असा काढता येईल :

म = २
आणि जर म = ३ असेल, तर हा आलेख असा काढता येईल :
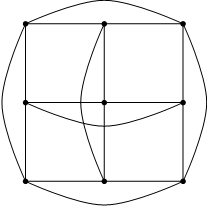
म = ३
जर म = ४ असेल, तर हा आलेख अगोदर काढून दाखवलाच आहे. जर म ५ किंवा ५ पेक्षा मोठा असेल तर हा आलेख काढणे गुंतागुंतीचे होईल, पण त्याची संकल्पना सहज करता येते. समजा म = ८. नेहमीच्या बुद्धिबळाच्या पटावरील चौरसांच्या ६४ मध्यबिंदूंना आपण खालीलप्रमाणे नावे देऊ या :
(१, ७), (२, ७), (३, ७), (४, ७), (५, ७), (६, ७), (७, ७), (८, ७)
(१, ६), (२, ६), (३, ६), (४, ६), (५, ६), (६, ६), (७, ६), (८, ६)
(१, ५), (२, ५), (३, ५), (४, ५), (५, ५), (६, ५), (७, ५), (८, ५)
(१, ४), (२, ४), (३, ४), (४, ४), (५, ४), (६, ४), (७, ४), (८, ४)
(१, ३), (२, ३), (३, ३), (४, ३), (५, ३), (६, ३), (७, ३), (८, ३)
(१, २), (२, २), (३, २), (४, २), (५, २), (६, २), (७, २), (८, २)
(१, १), (२, १), (३, १), (४, १), (५, १), (६, १), (७, १), (८, १).
बुद्धिबळात हत्तीची चाल कशी असते ते आपल्याला माहीत आहे : आडव्या सरळ रेषेत किंवा उभ्या सरळ रेषेत. जर ह्त्ती एका बिंदूकडून दुसऱ्या बिंदूकडे एका चालीत जाऊ शकत असेल, तर आपल्या आलेखात ते बिंदू एकमेकांचे शेजारी ठरतात.
अशाच प्रकारे म ही कोणतीही नैसर्गिक संख्या असेल, आणि आपण म x म या आकाराचा बुद्धिबळाचा पट मनात ठेवला तर हत्तीच्या चालीप्रमाणे बिंदूंचे शेजारी ठरतात.
श्रीखंडे यांनी असेही सिध्द केले की म ही ४ खेरीज दुसरी कोणतीही नैसर्गिक संख्या असेल तर वर निर्देशिलेले चार गुणधर्म बाळगणारा एकमेव आलेख असतो. ह्या आलेखाला म x म आकाराच्या बुद्धिबळातील हत्तीचा आलेख (m x m Rook’s graph) असे म्हणतात. प्राध्यापक श्रीखंडे यांची ही कामगिरी खूपच लक्षणीय होती.
प्रा. श्रीखंडे यांच्या संशोधनापैकी फक्त दोन महत्त्वाच्या गोष्टींसंबंधी मी लिहिले आहे. त्यांच्या या कामाचा जीवशास्त्र, वैद्यकशास्त्र, कृषिशास्त्र इत्यादी क्षेत्रातील प्रयोगांचे संकलन (Design of Experiments) करण्यात खूप उपयोग होतो. हा सांख्यिकीचा एक महत्त्वाचा भाग आहे. श्रीखंड्यांचे खूपसे काम समचयात्मक संकलनांबाबत (combinatorial designs) आहे. १९५०पासून सुमारे चाळीस वर्षे ते शोधनिबंध प्रकाशित करत राहिले. त्यांपैकी निवडक शोधनिबंधांचे पुस्तक कॅनडातील विनिपेग येथील चार्ल्स बॅबेज रिसर्च सेंटरने (Charles Babbage Research Centre) १९८५ साली प्रसिद्ध केले आहे. हे शोधनिबंध पाच भागांमध्ये विभागले असून प्रत्येक विभागाच्या सुरुवातीला स्वतः प्रा. श्रीखंडे यांचे भाष्य आहे. त्यामुळे वाचकाला त्यांची मर्मदृष्टी (insight) उपलब्ध होऊ शकते.
तर ह्या प्राध्यापक श्रीखंडे यांना भेटायला २०१२ साली मी व निर्मला आंध्र प्रदेशात आलो होतो. आमचा हा एक प्रकारचा भाविकपणाच होता. श्रीखंड्यांची मुलगी आशा कुलकर्णी हिचे अमेरिकेतील व्याही गुंटुरजवळ एक बऱ्यापैकी मोठे हॉस्पिटल चालवत होते. त्याच्या जवळच चिन्मयविजय आश्रम होता. श्रीखंड्यांना २०१० सालापासून तेथे राहण्याची सोय उपलब्ध झाली होती. माझे विग्यान युनिव्हर्सिटीतील व्याख्यान आटोपल्यावर त्या विद्यापीठाचे कुलगुरू आणि माझे जवळचे मित्र प्रा. गोवर्धन राव यांच्यासह आम्ही श्रीखंड्यांना भेटायला निघालो. त्यांच्यासाठी बरोबर काय न्यावे याचा थोडा विचार केला होता. काही मराठी मासिके, विशेषत: दिवाळी अंक, आणले होते, इतक्या दूरच्या प्रदेशात त्यांना मराठी संस्कृतीशी जवळीक साधता यावी या हेतूने. आम्ही सकाळी ११च्या सुमारास त्यांच्याकडे पोहोचलो तेव्हा ते इंग्लिशमधील एका भयकथेचे (horror story) पुस्तक वाचत होते. श्रीखंडे आम्हाला म्हणाले की आताशा अशी पुस्तके वाचण्यात त्यांचा वेळ बरा जातो. गणित आणि सांख्यिकी यांसंबंधी वाचन करणे त्यांनी सोडून दिले होते. साहजिकच होते ते. त्यावेळी त्यांचे वय होते ९४ वर्षे! ते सकाळ-संध्याकाळ बाहेरच्या पटांगणात सुमारे १५०० पावले चालत. त्यांच्याबरोबर आम्ही १-२ तास गप्पा मारल्या. त्यांनी आठवण करून करून सर्व परिचित व्यक्तींचे क्षेमकुशल विचारले. भूपेंद्र सिंहने केलेला चहा पिऊन आम्ही निघालो. जाताना भूपेंद्रचे आभार मानायला लागलो तर तो म्हणाला ‘ये सर तो मेरे दादाजी है। इनको छोडकर मै कही नही जाऊंगा।’ अशी काळजी घेणारा माणूस मिळणे विरळाच. श्रीखंडे पुण्या-मुंबईत असते तर आम्ही सर्वांनी मिळून जे केले असते ते तो एकटा बजावत होता.

भूपेंद्रसिंह
भूपेंद्र दिल्लीहून येताना फक्त दोन पिशव्या घेऊन श्रीखंड्यांच्याकडे आला. तेव्हा तो २१ वर्षांचा होता. फारसा शिकलेला नव्हता, त्याला हिंदीशिवाय कुठलीच भाषा येत नव्हती. हळूहळू श्रीखंड्यांनी त्याला इंग्लिश आणि मराठी या दोन्ही भाषा शिकवल्या, सुसंस्कृत बनवले, आणि मुख्य म्हणजे लळा लावला! तो त्याच्या या सरांना ‘माँ-बापसेभी ज्यादा’ मानू लागला. तो कुठे बाहेर गेला तर परत येईपर्यंत श्रीखंड्यांना काळजी लागून राहिलेली असे. श्रीखंडे म्हणायचे की भूपेंद्र त्यांचा आधार आहे, तर भूपेंद्र म्हणायचा श्रीखंडे सर त्याची ताकद आहेत. आलू-पालक आणि चपाती यांसारखे सरांना आवडणारे पदार्थ बनवून तो खाऊ घालत असे. दोघांची छान जोडी जमली होती.
पुन्हा श्रीखंड्यांना भेटायला जायचा विचार केला २०१६ साली. तेव्हा ते ९९ वर्षाचे होते. टेलिफोनवर त्यांना नीट ऐकू यायचे नाही. म्हणून संभाषण भूपेंद्रमार्फत व्हायचे. आम्ही येताना काय आणू असे विचारले तर श्रीखंड्यांनी ‘काहीही आणू नका, स्वत:शिवाय’ असे निक्षून सांगितले. निरिच्छपणाची कमाल झाली! यावेळी त्यांना भेटलो तेव्हा ते सुडोकूचे कोडे सोडवत होते. आता त्यांच्याने जास्त वाचवत पण नव्हते. भूपेंद्रने आम्हाला सांगितले की सुरुवातीच्या ४-५ वर्षांत ते अनाथालयातील आठवी-नववीच्या मुलींना गणित शिकवायचे, त्यांच्या गणितातील अडचणी सोडवायचे. पण आता सरांना ते शक्य होत नाही. एक-दीड तास गप्पा मारून, पुढील वर्षी त्यांच्या जन्मशताब्दीला आम्ही नक्की येऊ असे सांगून आम्ही त्यांचा निरोप घेतला. पण एक वर्ष संपायच्या आतच आम्ही पुन्हा तिकडे गेलो. कुणीतरी आम्हाला म्हटले होते की शंभर वर्षे पुरी व्हायची वाट बघू नका. पिकले पान गळायला मुहूर्त लागत नाही. जुलै २०१७ मध्ये तिकडे जाण्याआधी भूपेंद्रतर्फे पूर्वसूचना दिली होती. आमचे स्वागत करायला भूपेंद्र दाराशी आला तेव्हा म्हणाला की सकाळपासून सर तुमची वाट पाहत आहेत. पण आत जाऊन निर्मलाने जेव्हा काजूची बर्फी दिली आणि वाकून नमस्कार केला तेव्हा तिला उठवून ते म्हणाले, ‘आपण आधी भेटलो आहोत का कधी?’ माझ्या मनात चर्र झाले. ‘स्मृतिभ्रंशाद् बुद्धिनाशः’, म्हणजे माणसाला आठवेनासे झाले की त्याचे विचार करणेही संपते, ही गीतेतील उक्ती माझ्या चांगली ध्यानात होती. पण दोन-चार मिनिटांतच त्यांच्या चेहऱ्यावर ओळख पटल्याचे हास्य उमटले. आम्ही नेहमीप्रमाणे मोकळेपणी गप्पा मारल्या. त्यांनी आमच्या मुलींची, आमच्या नातवंडांची चौकशी केली, आणि स्वत:च्या पाचही नातींबद्दल भरभरून सांगितले. जवळजवळ ६० वर्षांपूर्वी न्यू यॉर्क टाइम्सच्या पहिल्या पानावर आलेला त्यांचा आणि त्यांच्या दोन सहकाऱ्यांचा फोटो त्यांच्या खोलीत लहानशा लाकडी फ्रेमवर लावला होता. तो त्यांनी आम्हाला दिला, त्यांची आठवण म्हणून. आम्ही निघाल्यावर निरोप द्यायला ते दोन चाकांच्या खुर्चीवरून (wheel chair) बाहेरपर्यंत आले, त्यांचा नेहमीचा अर्धा शर्ट आणि सुती पॅंट घालून. ते चित्र अजूनही माझ्या डोळ्यासमोर आहे. आमच्यासारखे, त्यांना भेटायला आलेले लोक जायला निघाले की श्रीखंड्यांना वाईट वाटत नसे. अमेरिकेहून आलेल्या नातेवाईकांच्या डोळ्यात पाणी बघितले की श्रीखंडेच त्यांची समजूत काढत आणि म्हणत, ‘तुम्हा सगळ्यांना तर परतलेच पाहिजे. तुमचे तिकडचे विश्व तुम्हीच निवडले आहे.’ आता काय म्हणायचे या निःसंग व्यक्तीला!

प्राध्यापक श्रीखंडे, जुलै २०१७
आम्ही मुद्दामच श्रीखंड्यांना शंभर वर्षे पुरी व्हायच्या तीन महिने आधी जाऊन भेटलो होतो. जन्मशताब्दीच्या दिवशी, म्हणजे १९ ऑक्टोबर २०१७ रोजी, सोहळा होणारच होता, आणि त्यांचे सर्व नातेवाईक, मित्रमंडळी जमणार होती. व्याख्याने होणार होती, केक कापला जाणार होता. पण त्या सगळ्यापेक्षा श्रीखंड्यांचे पुरे दोन तास, जे केवळ आम्हाला मिळाले होते, ते लाखमोलाचे होते. लग्नमुंजीचे बोलावणे असेल तर असाच विचार करून मी बरेच वेळा मुहुर्ताच्या काही दिवस किंवा महिनाभरही आधीच भेटून येतो. श्रीखंड्यांनी शंभरी तर पुरी केलीच. आणखी अडीच वर्षांनी २१ एप्रिल २०२० रोजी संध्याकाळी जेवण केल्यावर ते नेहमीप्रमाणे झोपायला गेले, आणि चिरनिद्रेच्या स्वाधीन झाले. यात डोळ्यांतून आसवे काढण्यासारखे काहीच नव्हते. आधीच्या दिवसापर्यंत त्यांनी सुडोकूचे कोडे सोडवले होते, त्यांची बुद्धी पुरी शाबूत होती. ते समाधानी आयुष्य जगले होते. आमच्या पुढच्या पिढीतील लोकांना कल्पनाही करवणार नाही की प्राध्यापक श्रीखंडे यांच्यासारखी उत्तुंग व्यक्ती या पृथ्वीतलावर शंभराहून जास्त वर्षे चालत फिरत होती.

प्रा. श्रीखंडे आणि निर्मला लिमये, जुलै २०१७

प्रा. श्रीखंडे आणि बालमोहन लिमये, जुलै २०१७
गेल्या महिन्यात, म्हणजे एप्रिल २०२१ मध्ये, प्राध्यापक श्रीखंडे यांचा पहिला स्मृतिदिन होता; आणि ६२ वर्षांपूर्वी एप्रिल महिन्यातच, त्यांनी ऑयलरचे अनुमान खोडून जगाला थक्क केले होते. परवा कुणी तरी म्हटले की गणित विषयात आंतरराष्ट्रीय कीर्ती मिळवणाऱ्या मराठी भाषिकांपैकी श्रीखंडे हे सर्वात पहिले. खरेच आहे ते. काही काळ तरी त्यांच्या सान्निध्यात यायचे भाग्य मला मिळाले. या उत्तुंग व्यक्तिमत्वाला माझी श्रद्धांजली, आणि त्यांनी केलेल्या कामाला माझा सलाम.
---
बालमोहन लिमये
(balmohan.limaye@gmail.com)
लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर निवृत्त. पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण
ललित लेखनाचा प्रकार
वाह! फारच सुंदर लेख!
लिमये सर, तुमचा प्रत्येक लेख अतिशय वाचनीय, तपशीलवार, माहितीपूर्ण, तरीही फारच साध्या शैलीत लिहिलेला असतो. प्रा. श्रीखंडे यांना मनःपूर्वक अभिवादन. त्यांच्या फोटोंमधील त्यांचे हास्य जे त्यांच्या तरुणपणी होते तसेच प्रत्येक फोटोत, अगदी आयुष्याच्या अखेरपर्यंत तस्सेच झळकते आहे. यावरून हा मनुष्य किती निरामय आयुष्य जगला असेल याची केवळ कल्पनाच करू शकतो. त्यांचे ऑयलरचे प्रमेय खोडणारे संशोधन तर थोर आहेच, ही हिमालयाच्या उंचीची माणसे सगळी! तुम्हीही, अर्थातच _/\_. असेच लिहीत रहा ही विनंती.
.
मनापासून केलेलं आणि अभ्यासपूर्ण लिखाण.
गणिताची अजूनही भीतीच वाटते पण असं लिहिलं की उत्साहानं वाचलं जातं. विशेषत: गणिताचे परिच्छेद सुरू होण्याआधी "हे नाही वाचलं तरी चालेल" अशी नीट सूचना आहे. त्यामुळे ते वाचलं. असंच जर पाठ्य पुस्तकांवर लिहिलं असतं समजुतीनं तर तीही मन लाऊन वाचली असती.
निर्मलाचा सहभाग
गणिताचा भाग सुलभ झाल्याच्या प्रतिक्रिया वाचून बरे वाटले. हा लेख लिहायला माझी पत्नी निर्मला हिने सुचवले होते. तो लिहितानाही तिचा संपूर्ण सहभाग होता. सर्व आकृती तिने काढल्या आहेत. आलेखशास्त्र हा माझ्या संशोधनाचा विषय नाही. तिने मात्र आलेखशास्त्रात संशोधन केले आहे. तिच्याशिवाय मी हा लेख लिहूच शकलो नसतो. सोप्यात सोपे कसे लिहावे हे देखील आम्ही एकमेकांशी बोलूनच ठरवत होतो.
लेख अतिशय आवडला
लेख अतिशय आवडला. त्यामागची कारणं इतरांनी दिलीच आहेत; त्यांचा पुनरुच्चार करत नाही.
प्राध्यापक लिमयांनी ‘हत्तीच्या आलेखा’चं वर्णन केलं आहे: म्हणजे बुद्धिबळाच्या पटावरच्या प्रत्येक घरासाठी कागदावर एक बिंदू काढायचा, आणि हत्ती जर अमुक घरातून तमुक घरात थेट जाऊ शकत असेल तर ते दोन बिंदू रेषेने जोडायचे. हत्ती पटावर कुठेही असला तरी तिथून एकूण चौदा घरांत जाऊ शकतो (उभ्या रेषेतली सात आणि आडव्या रेषेतली सात). याचाच अर्थ ह्या आलेखातला कुठलाही बिंदू इतर चौदा बिंदूंशी जोडलेला असतो.
पण ही कल्पना इतर मोहऱ्यांसाठीही राबवता येते. उदाहरणार्थ, हत्तीऐवजी घोडा वापरून असाच ‘तुरगालेख’ (knight’s graph) बनवता येतो. याबाबतीतला एक गंमतीदार प्रश्न म्हणजे सुरवातीला घोडा पटावर कुठेतरी ठेवून मग प्रत्येक घराला एकेकदा भेट देऊन मूळ घरात परत आणता येईल का? याला आलेखीय परिभाषेत Hamiltonian circuit म्हणतात. नेहमीच्या (म्हणजे ८ x ८ आकाराच्या) पटावर असं circuit शोधून काढता येतं. (कसं ते इथे लिहित नाही, पण इंटरनेटवर याचं वर्णन खूप ठिकाणी मिळेल.) पण समजा १९ x १४ असल्या आडनिड्या आकाराचा पट असेल तर काय होतं, कुठकुठल्या आकाराच्या पटावर असं circuit असू शकतं, हे आलेखशास्त्रात संशोधनाचे विषय असतात. (ह्या विशिष्ट प्रश्नाचं उत्तर ठाऊक आहे, पण समजा एखादा खूप किचकट आलेख असेल तर त्यावर Hamiltonian circuit आहे की नाही हे ठरवणं अवघड असतं. ठरवता आलं तर त्यावर लगेच शोधनिबंध लिहिण्याचा प्रघात आहे.)
लक्षात घेण्यासारखा एक फरक: आपण वर पाहिल्याप्रमाणे गजालेखातला प्रत्येक बिंदू इतर चौदा बिंदूंशी जोडलेला असतो. पण तुरगालेखाचं तसं नाही. घोडा जर पटाच्या कडेला आला तर तिथून जास्तीत जास्त चारच घरांत जाऊ शकतो, पण पटाच्या मधोमध असेल तर तिथून आठ घरांत जाऊ शकतो. नवशिक्या बुद्धिबळ खेळाडूंच्या मनावर हे ठसावं म्हणून अनुप्रास वगैरे वापरून याचं अगदी शाळकरी बोधवाक्यच बनवलेलं आहे: Knight on the rim is grim.
सर्वप्रथम, साष्टांग नमस्कार.
सर्वप्रथम, साष्टांग नमस्कार. बीएस्सीला असताना तुमचे आणि प्रा. घोरपडेंचे मल्टीव्हेरिएबल कॅल्क्युलस हे पुस्तक वाचले/सोडवले होते त्याची आठवण झाली. ते डॉ. लिमये म्हणजे तुम्हीच असाल असं मात्र माहित नव्हतं!
लेख उत्तम आहे. आम्हाला बीएस्सीच्या कॉलेजात डॉ. अभ्यंकर ह्यांच्याबद्दलच जास्त सांगितलं गेलं होतं. डॉ. श्रीखंडेंबद्दल मी खूप उशिरा, म्हणजे मुंबई विद्यापीठात प्रवेश मिळवल्यावर कळलं. मुंबई विद्यापीठाच्या गणित विभागाचे ते संस्थापक असल्यामुळे २०१८ हे वर्ष त्यांच्या शतकपूर्तीनिमित्त साजरे केले गेले होते. बाकी माहिती फारच त्रोटक माहित असल्यामुळे ती सर्वप्रथम इथेच कळली.
शुद्ध मराठीतला लेख प्रथम कठीण वाटला, पण नंतर कळलं की हे आलेख ६-रेग्युलर आलेखांचे प्रकार आहेत. अर्थात ग्राफ थिअरी ही साधारण adjacency matrices पर्यंतच शिकल्यामुळे पुढचं कळणं कठीण होतं.
अनेक आभार. धन्यवाद!
हृद्य परिचय
गणित विषयाच्या Combinatorics आणि Graph Theory ह्या शाखा कॉलेजात गणित शिकलेल्या विद्यार्थ्यास माहीत असतातच असे नाही, यद्यपि Permutations and Combinations (nPr आणि nCr), जे विषय आम्हास महाविद्यालयाच्या पहिल्या वर्षातच शिकविण्यात आले होते, ह्या शाखांची प्रवेशद्वारे आहेत असे म्हणता येते. Combinatorics आणि Graph Theory ह्या दोन्ही दालनांची दारे किलकिली उघडून त्यांच्या अंतरंगात काय काय दडलेले आहे ह्याची अल्प चुणूक प्रा. लिमयेंच्या लेखात दिसते आणि हे कार्य ’मणौ वज्रसमुत्कीर्णे सूत्रस्येवास्ति मे गति:’ अशा सौकर्याने घडवून आणल्याबद्दल त्यांचे आभार मानावेत तितके थोडेच आहे. हे करतांनाच त्या विषयांतील परात्पर गुरु डॉ श्रीखंडे ह्यांचाहि हृद्य परिचय लेखाने घडवून आणला आहे.
प्राचीन आणि मध्ययुगीन हिंदु शास्त्रांमध्ये मधून मधून ह्या विषयांना स्पर्श केला गेल्याचे जाणवते. पिंगलाच्या छन्द:शास्त्रामध्ये लघु (ल) आणि गुरु (ग) मात्रांचे (mora बहुवचन morae) वर्ण आपल्याला भेटतात. दिलेल्या संख्येच्या वर्णसमूहातील प्रत्येक वर्णाला लघु अथवा गुरु अशी मूल्ये दिल्यास त्यातून किती विविध रूपे निर्माण होतात अशी गणना पिंगलाने केली आहे. आयुर्वेदाने मानलेल्या षड्रसांपैकी कोणत्याहि २ अथवा ३,४,५ अशा रसांचे मिश्रण केल्यास किती नवे रस निर्माण होतात अशी गणना चरकाच्या चरकसंहितेमध्ये करण्यात आली आहे.
नरसिंहाचा पुत्र नारायणपण्डित ह्याने इ.स. १३५६ साली लिहिलेल्या 'गणितकौमुदी' ह्या ग्रन्थामध्ये व्यवहार (अध्याय) १३ हा 'अंकपाश' म्हणजे Combinatorics ह्याला वाहिलेला आहे आणि व्यवहार (अध्याय) १४ मध्ये 'Magic Squares' ची चर्चा केली आहे. नारायणपण्डित ह्यांनाच 'भद्रगणित' असे नाव देतो. न × न अशा कोष्टकामध्ये अंक अशा प्रकारे लिहावयाचे की प्रत्येक आडवी ओळ, प्रत्येक उभी ओळ आणि दोन्ही कर्ण ह्यांमधील अंकांचे संकलन (बेरीज) एकच संख्या असेल. (ह्यांना "भद्रगणित" ही उपाधि अशासाठी दिलेली असावी की अंक भरलेल्या आकृतींना यन्त्र असे नाव होते आणि अशी यन्त्रे बहुश: जादूटोण्याच्या कामात वापरत असत. आपले गणित तशा प्रकारचे नाही हे सूचित करण्यासाठी नारायणाने ’भद्र’ ह्या शब्दाचा उपयोग केला असावा.)
१२व्या शतकामध्ये निर्माण झालेल्या खजुराहो मंदिरसमूहामध्ये पार्श्वनाथाचे मंदिर आहे. त्यामधील ४ × ४ चा Magic Square येथे पाहता येतो. त्यातील अंक असे आहेत. संकलन ३४ आहे..
७ १२ १ १४
२ १३ ८ ११
१६ ३ १० ५
९ ६ १५ ४
येथील उभ्या ओळी, आडव्या ओळी, कर्ण ह्यांची बेरीज ३४ येते. तसेच शेजारशेजारचे कोणतेहि ४ आकडे घेतले तरीहि बेरीज ३४ येते. उदाहरणार्थ
१३ ८
३ १०.
It was very nice to know
It was very nice to know about such a great Indian Mathematician through your article sir. I really enjoyed reading about his fundamental contributions to Mathematics, which were described in a such simple words. Having a preview of Prof. Shrikhande's simple, caring, witty personality though your description itself was amusing to read.
प्रा. श्रीखंडे यांच्या कन्येकडून
प्रा. श्रीखंडे यांच्या कन्या आशा कुलकर्णी यांच्याकडून आलेला प्रतिसाद -
तुमचा लेख उत्तम झाला आहे. माझ्या वडिलांबाबतचा तुमचा दृष्टिकोन आणि त्यांच्याबद्दलच्या तुमच्या आठवणी एका मोठ्या वाचकवर्गापर्यंत पोचवण्याबद्दल खूप आभार. इतर वाचकांच्या प्रतिक्रिया पाहता तेदेखील माझ्याशी सहमत आहेत असे दिसते. मी हा लेख आमच्या विस्तारित कुटुंबांकडे पाठवला. त्यांच्या मते हे लेखन माहितीपूर्ण आहेच, शिवाय इतके नितळ, रोचक आणि हृदयस्पर्शी आहे की ते एक समृद्ध आदरांजली ठरते. तसेच हे एखाद्या टाइम कॅप्सूलप्रमाणे आहे. कुटुंबियांना माहीत नसलेल्या अनेक गोष्टी त्यामुळे प्रकाशात आल्या आहेत.
या लेखनासाठी तुम्ही घेतलेल्या कष्टांचे मला खरोखरच कौतुक वाटते. माझ्या वडिलांबद्दल तुम्हाला आणि तुमच्या पत्नीला खूप स्नेहभाव वाटतो हे स्पष्ट दिसते. हे खचितच खूप प्रेमाने केलेले काम आहे. पुन्हा एकदा आपले आभार.
हे अस काही वाचल
हे अस काही वाचल की आपल जीवन किती व्यर्थ आहे ते खुपच खोलवर जाणवत. नतमस्तक प्राध्यापक श्रीखंडे यांच्यासमोर आणि तुमच्या देखील!
इथे बरेच गणितात प्रविण लोक आहेत म्हणुन माझे एक दोन अगदी बेसिक प्रश्न विचारतो. जमल्यास कुणीतरी प्लीज उत्तरे द्या.
१. एखाद्या संखेला दुसऱ्या संखेच्या डोक्यावर चढवणे म्हणजे नक्की काय? xy?
नॅचरल संख्यान्च्या बाबतीत अर्थ स्प्ष्ट आहे की x ला y वेळा स्व:ताशीच गुणायचे (for example 102 = 100)
जेव्हा y निगेटिव्ह असतो तेव्हा ही क्लियर आहे (for example 10-2 = 0.01)
जेव्हा y रॅशनल असतो तेव्हा ही क्लियर आहे (for example 102.5 = 105 * sqroot(10))
पण जेव्हा y ईरॅशनल असतो तेव्हा काय? त्याला कसे ईंटरप्रिट करायचे?
जेव्हा दोन्हि x, y ईरॅशनल असतील तेव्हा काय?
समजा y ईमॅजिनरी असेल तेव्हा काय?
मला माहीती आहे की माझे प्रश्न अगदीच बेसिक आहेत आणि आता खुप लाज वाटते की ऑयलरची आयडेंटीटी खरी कधी कळलीच नाही ते.
२. ट्रान्सेंडेंटल ईरॅशनल म्हणजे नक्की काय? सामान्य ईरॅशनल पेक्शा ते वेगळे कसे काय?
३. १/३ = ०.३३३३.... ही संख्या ईरॅशनल नाही (कारण १/३) आणि १/३ = ०.३४
(कारण एखाद्या संख्या दुसर्या संखेच्या कितीही जवळ नेउन ठेवु शकता आणि एकदा का तितकी जवळ नेली की कमीत कमी तितकी जवळ राहते) हे माझे इंटरप्रिटेशन बरोबर आहे का?
प्रतिसादांची संख्या २३
प्रतिसादांची संख्या २३ माझे प्रश्न मुळ राहू नयेत म्हणुन अजुन एक वाढवायला हा एक प्रश्न.
समजा क्वांटम थियरीची मल्टायवर्स ईंटर्प्रिटेशन बरोबर आहे अस धरून चालु. समजा आपण अशा एखाद्या युनिवर्स मध्ये उडी मारली की ज्यात बाकी सर्व सारखे आहे पण पाय चा बरोब्बर एक डिजिट ट्रीलियन्थ ट्रीलियन्थ जागेवर वेगळा आहे. तर आपल्याला तो वेगळेपणा जाणवेल का? नाहीजरी जाणवला तरी असा काही फरक आहे का हे काही मार्गाने शोधता येईल का?
यावर एखादे साय फाय पुस्तक आहे का?
मोघम उत्तरे
तांत्रिक गुंतागुंतीत अडकून न पडता आणि मराठीचा अत्याग्रह न धरता काहीशी मोघम उत्तरं देतो.
> x^y? पण जेव्हा y ईरॅशनल असतो तेव्हा काय? त्याला कसे ईंटरप्रिट करायचे?
एक मार्ग म्हणजे लिमिट ही संकल्पना वापरणे. उदा. y = २ चे वर्गमूळ समजा. इथे y इरॅशनल आहे. पण रॅशनल संख्या वापरून y च्या हवं तितकं जवळ जाता येतं. उदा. y च्या जागी 1.4, 1.41, 1.414 अशा संख्या वापरून दरवेळी x^y काढायचा आणि या सीक्वेन्सचं लिमिट घ्यायचं. इथे x इरॅशनल असला तरी बिघडत नाही पण तुम्हाला x इरॅशनल असणं खुपत असेल तर x च्याही जागा असा approximating sequence वापरा.
२. ट्रान्सेंडेंटल ईरॅशनल म्हणजे नक्की काय? सामान्य ईरॅशनल पेक्शा ते वेगळे कसे काय?
उदाहरणार्थ, y = २ चे वर्गमूळ हा अल्जिब्राईक इरॅशनल आहे, कारण y^2 =2 अशा प्रकारच्या बीजगणिती समीकरणात तो बसतो. पण उदाहरणार्थ, 'पाय' (म्हणजे वर्तुळाच्या परीघाचं आणि व्यासाचं गुणोत्तर) हा ट्रान्सेंडेंटल ईरॅशनल आहे, कारण अशा प्रकारच्या कुठल्याही बीजगणिती समीकरणात तो बसत नाही. (पण ह्याची सिद्धता अवघड आहे, तेव्हा प्लीज माझ्यावर विश्वास ठेवा.) असे 'पाय' सारखे ट्रान्सेंडेंटल ईरॅशनल बरेच आहेत (खरं म्हणजे अनंत आहेत), पण 'पाय' आणि Euler constant e वगळता ते सर्वसाधारणपणे कॉलेजपर्यंतच्या गणितात फारसे पाहायला मिळत नाहीत.
३. १/३ = ०.३३३३.... ही संख्या ईरॅशनल नाही (कारण १/३) आणि १/३ = ०.३४
(कारण एखाद्या संख्या दुसर्या संखेच्या कितीही जवळ नेउन ठेवु शकता आणि एकदा का तितकी जवळ नेली की कमीत कमी तितकी जवळ राहते) हे माझे इंटरप्रिटेशन बरोबर आहे का?
ही इरॅशनल नाही (किंवा रॅशनल आहे) हे बरोबर आहे, पण त्यासाठी १/३ हे १ आणि ३ चं गुणोत्तर आहे इतकं कारण पुरे आहे. अशा कुठल्याही दोन नैसर्गिक संख्या घेतल्या तरी त्यांचं गुणोत्तर रॅशनल असतं: उदाहरणार्थ, ३७/११३ वगैरे. मात्र जवळ नेण्या न नेण्याशी या संकल्पनेचा काही संबंध नाही.
वा वा वा
उत्तरे इतक्या तत्परतेने दिल्याबद्दल धन्यवाद!
१. हे एकदमच पटले! पण आता मला एक ईंटरप्रिट करायचा मार्ग मिळाल्यावर अजुन एखादा मार्ग जो कि कॅलक्युलस ची पळवाट ने घेता (जसे की आय एम ओ च्या परीक्षार्थी साठी असतो) मिळाला तर बरे होईल. मी स्वत: पण यावर विचार करेनच.
२. पाय आणि ई हे दोह्नी ट्रान्सेंडेंटल ईरॅशनल आहेत हे मी विकि वर पाहीलेला होतच. किंबहुना हा प्रश्न ही त्यातुनच आला. पण विकिवर दिलेल स्प्ष्टीकरण काही मला झेपल नव्हत. त्यामुळे या स्प्ष्टीकरण बद्दल धन्यवाद.
> (पण ह्याची सिद्धता अवघड आहे, तेव्हा प्लीज माझ्यावर विश्वास ठेवा.)
तो तर आहेच हो! तुम्ही टेन्युअर्ड प्राध्यापक तेव्हा माझी काय बिशाद?
पण जस्ट प्लेयिंग डेविल्स ॲड्वोकेट. पाय पण बीजगणिती समीकरणात बसेल ना? (याच उत्तर नाही हे माहीती असून विचारायच धाडस करत आहे)
कारण की पाय = परीघ / व्यास, हे एक बीजगणितीय समीकरण असल्यासारखे वाटत आहे (पण एकिकडे सर्क्युलर आर्ग्युमेंट असल्यासारखे पण वाटत आहे)
३. त्यासाठी १/३ हे १ आणि ३ चं गुणोत्तर आहे इतकं कारण पुरे आहे
अगदी बरोबर. ते ॲक्च्युली दोन प्रश्न होते.
मी काही काळापुर्वी प्रिंस्टन कंपॅनियन टु मॅथ्स् चा काही भाग वाचुन काढला (Parts I, II, VI, VII, VIII, and selective reading from III, IV and V). प्रश्न सुटायच्या आइवजी अजुनच वाढले आणि आता तर साध्या साध्या कॉन्सेप्ट्स वर देखील प्रश्न पडायला लागले आहेत.
लिमिट वेगळं, कॅल्क्युलस वेगळं
त्याचं असं आहे की कॉलेजमध्ये गणित शिकताना आपण पहिल्यांदा limit ही संकल्पना शिकतो, आणि मग differential/integral calculus शिकतो. आता calculus मध्ये limit ही संकल्पना राबवली जात असल्यामुळे ‘ते सगळं एकच’ अशी समजूत होऊ शकते. पण वास्तविक तसं नाही. प्रत्यक्षात limit ही अधिक व्यापक (आणि एका अर्थाने अधिक मूलगामी) संकल्पना आहे. वर x^y बद्दल जे मी लिहिलं आहे त्यात limit येतं, पण differential calculus नाही. नॅचरल लॉगॅरिथमचं तसंच आहे. लिमिट वापरून त्याची व्याख्या करता येते: The limit of (a^x-1)/x as x goes to zero is ln(a), which is the natural logarithm of the number a. यात लिमिट आहे पण differential calculus ची गरज नाही.
वर मी बीजगणिती समीकरण म्हणालो त्याला इथे विशिष्ट अर्थ आहे: उदाहरणार्थ, x^2 - x + 2=0 किंवा x^3-4x^2 + 7 x + 5=0 अशा छापाचं समीकरण. यात ‘पाय’ किंवा ‘ई’ बसत नाही. दोन्ही सिद्धता अवघडच आहेत, पण (माझ्या मते) ‘पाय’ ची जास्त अवघड आहे.

खूप छान परिचय लेख.
धन्यवाद सर. गणितातील उदाहरणे पुन्हा वाचावी लागणार आहेत.