गणिताच्या निमित्ताने – भाग ५

बालमोहन लिमये

('ज्या विषयात मी कधीच संशोधन केले नव्हते त्या विषयात एका विद्यार्थ्याचा वाटाड्या मला बनायचे होते.' प्रा. बालमोहन लिमये, पीएच. डी. च्या आपल्या पहिल्या विद्यार्थ्याविषयी. त्याशिवाय या भागात, रंगीत नकाशाचा प्रश्न : नकाशा रंगवायला किती रंग लागतील? प्रा. बालमोहन लिमये यांच्या साप्ताहिक लेखमालेतील मागील भाग इथे.)

पीएच. डी.चा पहिला विद्यार्थी

१९७५ साली मी आय. आय. टी. बॉंम्बेच्या गणित विभागात सहायक प्राध्यापक (Assistant Professor) म्हणून रुजू झालो. माझ्या सुरुवातीच्या वर्षांत मी ज्यांच्याबरोबर संशोधनविषयक आदान-प्रदान करू शकेन असे गणित विभागात दोन-चार जणच होते. त्यापैकी काहींनी एकत्र येऊन एक साप्ताहिक चर्चासत्र सुरू करायचे ठरवले. पण सगळ्यांच्या संशोधनाचे विषय वेगळेवेगळे होते. तेव्हा सर्वांना रस वाटेल असा चर्चेचा विषय निवडणे जरूर होते. बरीच सल्ला-मसलत करुन पीटर डेम्बोम्वस्की या गणितज्ञाने १९६८ साली लिहिलेल्या Finite Geometries, म्हणजे सान्त भूमिती, या पुस्तकाच्या आधारे दर आठवड्याला एकेकाने बोलायचे ठरले. मी, माझी पत्नी निर्मला, डॉ. गिरीश पटवर्धन यांच्या देखरेखीखाली पीएच. डी. करणारा शरद साने यांनी व्याख्याने दिली. त्याशिवाय डॉ. कपिल जोशी व श्री. बी. डी. खानवेलकर उपस्थित राहून चर्चेत भाग घेत असत.

हा प्रयोग काही महिने चालल्यावर १९७६ साली डॉ. पटवर्धनांना दोन वर्षांसाठी इराकमधील एका विद्यापीठात जायची संधी प्राप्त झाली. त्यामुळे आमचे चर्चासत्र कसे चालू ठेवायचे आणि मुख्यत: शरद सानेचे मार्गदर्शन कुणी करायचे असे प्रश्न उद्भवले. शरद सानेला विश्वासात घेऊन पटवर्धनांनी मलाच याबद्दल विचारणा केली. खरे म्हणजे त्यांचे संशोधन समचयशास्त्र (Combinatorics) या विषयात होते, माझ्या विषयापेक्षा अगदी वेगळे. परंतु त्यांच्या विषयाचा आमच्या चर्चासत्रातील काही भागांशी जवळचा संबंध होता. शरद सानेच्या पीएच. डी.च्या अभ्यासक्रमातील काही वर्षे वाया जाऊ नयेत या हेतूने मी औपचारिक होकार दिला. तेव्हा तरी पटवर्धनांनी इराकहून सानेचे मार्गदर्शन सुरू ठेवायचे, पण दर महिन्याला शरद सानेचे काम सुरू असल्याची खातरजमा मी करायची एवढीच बोली होती.

आय. आय. टी. बॉम्बेच्या नियमाप्रमाणे फक्त एक वर्षभर असे लांबून मार्गदर्शन करता येते. पण त्यापेक्षा जास्त कालावधी लागणार असला, तर मार्गदर्शकच बदलावा लागतो. पटवर्धनांची इराकमधील नेमणूक दोन वर्षांची असल्याने मी पुन्हा कात्रीत सापडलो. शेवटी मी शरद सानेचा मार्गदर्शक व्हायचे मान्य केले. ही फारच मोठी जबाबदारी होती, ज्या विषयात मी कधीच संशोधन केले नव्हते त्या विषयात एका विद्यार्थ्याचा वाटाड्या मला बनायचे होते. परंतु आमच्या Finite Geometriesवरील चर्चासत्रात शरद सानेने खूप उत्साहाने भाग घेतला होता, आणि त्यातील काही भाग माझी पत्नी निर्मला हिच्या प्रक्षेप भूमिती (Projective Geometry) या विषयातील संशोधनाशी निगडित होता. सारासार विचार करून मी मनाचा हिय्या केला. पटवर्धनांनी इराककडे कूच केल्यावर मी शरद सानेला निर्मलाने तिच्या पीएच. डी.साठी लिहिलेला प्रबंध वाचायला सांगितला. त्याने तो वाचला, आणि तो Projective H-Planes याबद्दल सखोल अभ्यास करू लागला. त्याच्या पीएच. डी. अभ्यासाला आता एक वेगळेच वळण लागले होते. पण तसे वळण घेतल्यावर मार्गक्रम कसा असेल हे फारच अनिश्चित होते.

तेवढ्यात १९७७ साली मी स्वत: बंगलोरमधील भारतीय विज्ञान संस्थान (Indian Institute of Science) या ठिकाणी मुंबईतील टिफ्र (TIFR: Tata Institute of Fundamental Research) या संस्थेने चालवलेल्या उपयोज्य गणित (Applicable Mathematics) या कार्यक्रमामध्ये दोन महिन्यांचा अभ्यासक्रम शिकवण्याचे मान्य केले. शरद साने माझ्याबरोबर बंगलोरला आला. तो दररोज काही नवीन गोष्टी शोधत होता, त्या लिहून काढत होता व मला वाचायला देत होता. मी माझे अभिप्राय त्याला देत असे, पण त्यानंतर त्याचे त्यालाच पुढे जायचे होते. त्याला माहीत होते की समचयात्मक संरचना (combinatorial structures) आणि भूमितीय संरचना (geometric structures) यांमध्ये घनिष्ठ संबंध आहेत. त्याने डॉ. पटवर्धनांबरोबर सुरू केलेले काम समचयात्मक असल्याने त्या कामाचे भूमितीय संरचनांशी नाते जोडणे सोपे गेले. त्याने तशी नवीन नाती शोधूनही काढली. इतकेच नव्हे तर डेम्बोवस्कीच्या पुस्तकातील H-Planes संबधीचे विधान एका बाबतीत चुकीचे आहे व बाकीच्या बाबतीत ते जास्त बळकट करता येते असे त्याच्या लक्षात आले. नेमके उदाहरण देऊन त्याने ती चूक सिद्ध केली. या सगळ्यामुळे त्याला हुरूप आला. आम्ही जेव्हा बंगलोरहून मुंबईला परतलो तेव्हा तो खूप उत्साहात होता.

मुंबईला येताच त्याला एका अनपेक्षित गोष्टीचा सामना करावा लागला. मधल्या काळात प्राध्यापक वर्तक यांची गणितविभागाच्या प्रमुखपदाची मुदत संपली होती, आणि नव्या प्रमुखांचा इरादा असा होता की शरद सानेला स्वत:कडे पीएच. डी.चा विद्यार्थी म्हणून घ्यायचे. शरद सानेला हे बिलकुल मान्य नव्हते. त्याने सरळ आय. आय. टी.तील शैक्षणिक कार्यक्रमांचे संकायाध्यक्ष (Dean, Academic Affairs) यांच्याकडे दाद मागितली. त्यांनी गणित विभागाच्या पदव्युत्तर समितीची बैठक बोलावली. विभागप्रमुखांना त्यांचा इरादा मागे घ्यावा लागला. हे चालू असतानाच शरद सानेने एक शोधनिबंध लिहिला, आणि त्यावर लेखक म्हणून त्याचे व माझे अशी दोन नावे घातली. मी तो निबंध वाचून काही सूचना केल्या असल्या तरी माझे संशोधनात्मक योगदान किमानच होते. यामुळे लेखक म्हणून आपले नाव घालू देणे खरे म्हणजे मला मान्य नव्हते. पण एकदा का आमचा संयुक्त पेपर प्रसिद्ध झाला की त्याला माझ्यापासून हिरावून घेणे कोणालाही जमणार नाही असे मानून शरदने हट्ट धरला. लवकरच आमचा संयुक्त शोधनिबंध Journal of Combinatorics, Information and System Sciences मध्ये १९७८ साली प्रकाशित झाला.

त्यानंतर शरद साने एकामागून एक नवीन शोध लावू लागला. मला सुधीर कुलकर्णी, नारायण नंबूदिरी आणि रेखा कुलकर्णी या माझ्या विषयात पीएच. डी. करणाऱ्या विद्यार्थ्यांच्या कामावर लक्ष ठेवायचे होते. तरीही सानेचे लिखाण वाचून मी ते संमत करत गेलो. असे बरेच सिद्धांत जमल्यावर मला ठरवायचे होते की आतापर्यंत सानेने केलेले काम पीएच. डी.साठी पुरेसे आहे की नाही. पण या नव्या विषयातील माझा आवाका मर्यादित होता. म्हणून मी सानेचे काम या विषयातील जागतिक मान्यता पावलेल्या डेव्हीड ड्रेक या ख्यातनाम गणितज्ञाकडे पाठवले. त्याच्याकडून निर्वाळा आल्यावर मी सानेला त्याचा पीएच. डी.चा प्रबंध लिहून आय. आय. टी.ला सादर करायला सांगितले. परदेशी व भारतीय अशा दोन्ही परीक्षकांनी तो प्रबंध वाखाणला. शरदच्या प्रबंधाचे समर्थन (thesis defence) २० नोव्हेंबर १९७८ रोजी ठरले होते. तो त्याचा वाढदिवसही होता. कर्मधर्मसंयोग असा की आदल्या दिवशीच प्रा. पटवर्धन इराकहून परतले होते. तेसुद्धा सानेच्या तोंडी परीक्षेला उपस्थित राहिले. ती संपल्यावर सानेच्या प्रबंधावर स्वाक्षऱ्या झाल्या, माझी मार्गदर्शक म्हणून, प्रा. पटवर्धनांची सहमार्गदर्शक म्हणून आणि टिफ्रमधील प्रा. नवीन सिंघी यांची परीक्षक म्हणून.

या निमित्ताने एक गंमत आठवली. या आधी पॉल एर्डिश या गणितज्ञांचा उल्लेख मी केला आहे. हे हंगेरियन गणितज्ञ विसाव्या शतकातील सर्वात बहुप्रसव (prolific) मानले जातात. त्यांनी १५०० पेक्षा जास्त शोधनिबंध प्रसिद्ध केले आहेत. पण सर्वात आगळी गोष्ट म्हणजे त्यांचे ५०० हून अधिक सहलेखक आहेत. एर्डिश देशोदेशी फिरायचे. आपल्या मनातले प्रश्न इतरांना सांगायचे आणि कसून चर्चा करायचे; उत्तरे सापडली की त्यावर आधारित शोधनिबंध लिहायला सहसंशोधकाला सांगून स्वत: पुढच्या ठिकाणी रवाना व्हायचे. जवळची एकच सूटकेस हीच त्यांची सगळी मालमत्ता होती. एर्डिशचे आपण सहलेखक आहोत की नाही आणि नसलो तर त्यांच्यापासून शोधनिबंध लिहिण्याच्या बाबतीत आपण किती दूर आहोत हे ठरवण्यासाठी ‘एर्डिश नंबर‘ ही संकल्पना प्रचलित आहे. एर्डिशचा स्वत:चा नंबर ०, आणि त्यांच्या सगळ्या सहलेखकांचा एर्डिश नंबर १. उदाहरणार्थ, माझे मित्र तरलोक नाथ शोरी आणि नवीन सिंघी या दोघांनी एर्डिशबरोबर पेपर लिहिला असल्याने दोघांचाही एर्डिश नंबर १. एखादा गणिती एर्डिशचा सहलेखक नसेल पण त्यांच्या सहलेखकांपैकी कुणाचा सहलेखक असेल तर त्याचा एर्डिश नंबर २. असे पुढे पुढे जात प्रत्येकाने आपला एर्डिश नंबर काढायचा.

१९८१ साली शरद साने आणि नवीन सिंघी यांनी एक संयुक्त शोधनिबंध लिहिला. त्यामुळे शरद सानेचा एर्डिश नंबर २ झाला आणि आपोआप माझा एर्डिश नंबर ३ झाला, कारण मी आणि साने यांच्या नावे एक शोधनिबंध आधीच प्रसिद्ध झाला होता. त्याबरोबर माझी पत्नी निर्मला हिचा एर्डिश नंबर ४ झाला, कारण आम्ही दोघांनी पूर्वी संयुक्त शोधनिबंध लिहिला होता. काही वर्षांनंतर, १९८७ साली शरद साने आणि निर्मला मुंबई विद्यापीठात शिकवत असताना एका शोधनिबंधाचे सहलेखक झाले. यामुळे निर्मलाचाही एर्डिश नंबर ३ झाला. आहे की नाही गंमत! अमेरिकेतील ओकलंड विद्यापीठाने The Erdós Number Project अशी वेबसाइट सुरू ठेवली आहे. आजपर्यंत जवळजवळ २७०,००० गणितज्ञांना एर्डिश नंबर प्राप्त झाला आहे. केवढा हा परिवार!

शरदच्या संशोधनाला वेग आला. शरदचा आणि सुनीता पुराणिक हिचा १९८० साली विवाह झाला. सुनीताने आमच्याच गणितविभागात पीएच. डी. पूर्ण केली होती. तीही गणित व संगणकशास्त्र शिकवायची. वर्षभरानंतर त्यांना मुलगा झाला, त्याचे नाव त्यांनी ठेवले सारंग; सगळा ‘स’चा मामला. आई-वडिलांसह आपल्या कुटुंबाची जबाबदारी पेलत शरदने आपले मुंबई विद्यापीठात अध्यापन आणि संशोधनाचे काम नेटाने चालू ठेवले. त्याचे उत्तम शोधनिबंध गणित विषयाच्या उत्कृष्ट नियतकालिकांमध्ये प्रसिद्ध होत गेले. शरदची भराभर पदोन्नती होत जाऊन अल्प काळात तो पूर्ण प्राध्यापक (full professor) झाला. १९९१ साली शरद साने आणि मोहन श्रीखंडे यांनी ‘Quasi-Symmetric Designs’ या नावाचे पुस्तक लिहिले. ते लंडन मॅथेमॅटिकल सोसायटीच्या ‘लेक्चर नोट्स सेरीज’मध्ये केंब्रिज युनिव्हर्सिटी प्रेसने प्रसिद्ध केले. मोहन हा सुप्रसिद्ध गणितज्ञ आणि संख्याशास्त्रज्ञ प्राध्यापक एस. एस. श्रीखंडे यांचा मुलगा. मला शरदने त्या दोघांनी लिहिलेल्या पुस्तकाची एक प्रत भेट म्हणून दिली. ती उघडून पाहिली आणि आश्चर्यचकित झालो. ते पुस्तक मोहनने आपली पत्नी नीलिमा आणि मुलगी अदिति यांना समर्पित केले होते, तर शरदने मला. मी त्याला म्हटले, ‘शरद, तुझी पत्नी सुनीता आणि मुलगा सारंग यांची परवानगी घेतली होतीस ना?’ शरद म्हणाला, ‘हो, त्याची काळजी नाही. शिवाय ही माझी पावती आहे, तुम्ही माझ्यात बाणावलेल्या गणिती शिस्तीबद्दलची! दुसरे कोणीही ती नाकारू शकत नाही.’

गेल्या २५ वर्षांत आमच्या गणितविभागातून पदवी मिळवलेल्या ज्या दोन-चार विद्यार्थ्यांना आय. आय. टी.ने विशिष्ट पूर्वछात्र पुरस्कार (Distinguished Alumnus Award) बहाल केला आहे, त्यांपैकी एक आहे शरद साने. २०१० साली तो मुंबई विद्यापीठातून निवृत्त झाला. त्यानंतर काही महिन्यांनी फेब्रुवारी २०११ मध्ये योजलेल्या छोट्याशा समारंभाला मी गेलो होतो. तेव्हा मी सांगितलेली एकच गोष्ट मला अजून आठवते : ‘शिष्यात् इच्छेत् पराजयम्।’ म्हणजे शिष्य आपल्यापेक्षा सरस व्हावा अशी इच्छा धरावी. माझी इच्छा पुरी झाली होती.

शरद साने आणि पत्नी सुनीता, फेब्रुवारी २०११

---

रंगीत नकाशा

आपल्या सगळ्यांनाच नकाशा रंगीत असेल तर तो बघायला आवडतो. वेगवेगळ्या प्रदेशांच्या सीमा दुरूनही डोळ्यात भराव्या म्हणून शेजारच्या प्रदेशांना वेगळे रंग वापरतात. प्रश्न असा निर्माण होतो की नकाशा असा रंगवायचा असला तर किती रंग लागतील? प्रदेशांची संख्या वाढली तर रंग पण जास्त वापरावे लागतील, का चार रंग नेहमीच पुरेसे होतील असा प्रश्न इंग्लंड मधील फ्रॅन्सिस व फ्रेडेरिक गथ्री (Francis and Frederick Guthrie) या भावांना १८५२ साली पडला होता. त्यांना आढळून आले की नकाशात कितीही प्रदेश असले तरी चारच रंग पुरतात, अगदी नेहमी समुद्राला देण्यात येणारा निळा रंग धरूनसुद्धा. पण तसे ते सिद्ध करू शकत नव्हते. एवढे मात्र निश्चित होते की तीन रंग पुरत नाहीत. आपल्याकडचेच एक उदाहरण घेऊ या. समजा आपल्याला भारतातील सहा राज्यांचा रंगीत नकाशा काढायचा आहे, राजस्थान, गुजरात, महाराष्ट्र, छत्तीसगड, उत्तर प्रदेश आणि मध्यप्रदेश यांचा, आणि आपल्याकडे निळा, तांबडा व पिवळा असे तीन रंग आहेत.

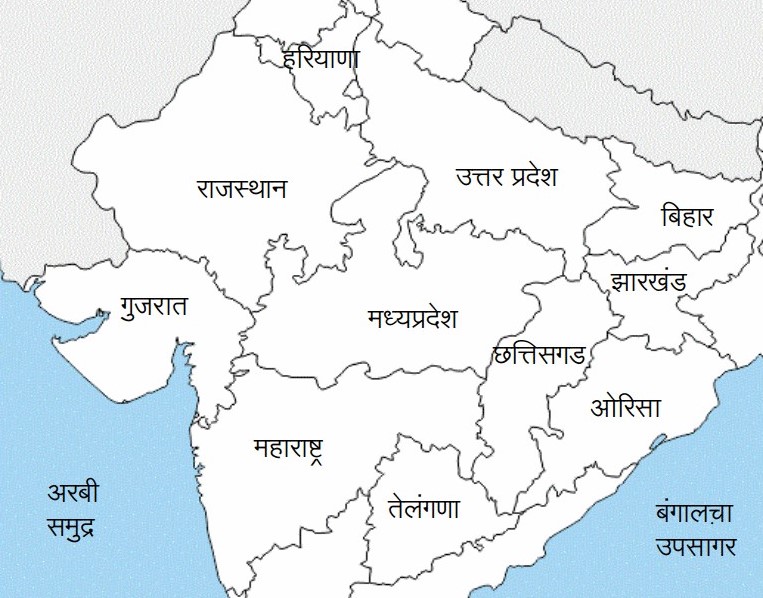
रंग न दिलेला भारतातील काही राज्यांचा नकाशा

मध्यप्रदेश नावाप्रमाणे मध्यवर्ती आहे आणि त्याच्या सीमेचा काही भाग इतर पाचही राज्यांच्या सीमांशी सामाईक आहे. त्याला आपल्याकडील तीन रंगांपैकी कुठला तरी एक रंग द्यायला हवा; समजा आपण निळा रंग दिला. आता या सहा राज्यांपैकी दुसऱ्या कोणत्याच राज्याला निळा रंग देता येणार नाही. राजस्थानला आपल्याकडे उरलेल्या दोन रंगांपैकी कुठला तरी एक द्यायला हवा; समजा आपण तांबडा रंग दिला. मग गुजरात आणि उत्तर प्रदेश यांना उरलेला पिवळा रंग द्यावा लागेल, कारण ही दोन राज्ये जशी मध्यप्रदेशाला लागून आहेत, तशी राजस्थानलादेखील लागून आहेत. नंतर महाराष्ट्राला तांबडा रंग देणे भाग आहे, कारण महाराष्ट्राच्या सीमेचा काही भाग जसा मध्यप्रदेशाच्या सीमेशी सामाईक आहे तसा गुजरातच्या सीमेशीही सामाईक आहे. शेवटी प्रश्न उरतो छत्तीसगड राज्याचा. त्याला आतापर्यंत वापरलेल्या निळा, तांबडा व पिवळा यापैकी कुठलाच रंग देता येणार नाही, कारण छत्तीसगड राज्याच्या सीमेचा काही भाग मध्यप्रदेश, महाराष्ट्र व उत्तर प्रदेश या तिन्ही राज्यांच्या सीमांशी सामाईक आहे. म्हणजे आपला सहा राज्यांचा नकाशा रंगवण्यासाठी तीन रंग पुरेसे नाहीत; आपल्याला चौथा रंग वापरावाच लागतो. आपण केलेल्या रंगसंगतीवरून लक्षात येईल की वरील सहा राज्यांच्या बाहेरील हरियाणा, बिहार, तेलंगणा अशा कित्येक राज्यांना आपण मध्यप्रदेशाला दिलेला म्हणजे निळा रंग देऊ शकतो. (शिवाय समुद्रकिनारा असणाऱ्या गुजराथ व महाराष्ट्र या राज्यांना दिलेले रंग समुद्राला दिलेल्या निळ्या रंगापेक्षा वेगळे आहेत, हे लक्षात घेतले पाहिजे.) यावरून किती रंग वापरावे लागतात हे फक्त प्रदेशांच्या संख्येवरच अवलंबून नसते हे दिसून येते. खालील चित्रांवरून ही गोष्ट अधिक स्पष्ट होईल. त्यांपैकी पंचकोनी चित्र आताच वर्णन केलेल्या सहा राज्यांच्या रंगसंगतीशी निगडित आहे. छत्तीसगड राज्याला हिरवा किंवा तसा कुठला तरी चौथा रंग देणे आपल्याला भाग पडले होते.

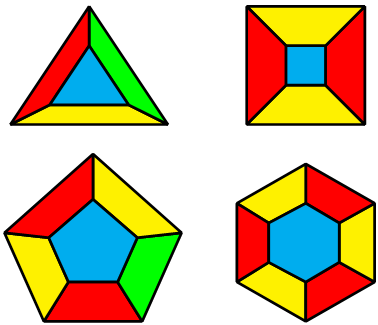
आकृती १

नकाशातील कुठल्याही दोन प्रदेशांमध्ये जर एखादी सामाईक सीमारेषा असेल तर त्या दोन प्रदेशांना वेगळे रंग देणे याला आपण नकाशा ‘उचित रीतीने’ रंगवणे असे म्हणू या.
चार रंग वापरून उचित रीतीने काढलेला जगाचा (जरा जुन्या काळचा) नकाशा खाली दिला आहे. समुद्राला निळा रंग दिला असल्याने समुद्रकिनारा असणाऱ्या कुठल्याही देशाला निळ्या रंगाखेरीज तीन रंगांपैकी एक रंग देणे जरूर असते. फक्त भूप्रदेशांनी वेढलेल्या (landlocked) देशांना मात्र समुद्राचा निळा रंग देता येतो. बाजारात किंवा ऑनलाइन मिळणाऱ्या नकाशात अशी काळजी सामान्यत: घेतलेली नसते. त्यामुळे हा नकाशा मिळवायला जरा त्रास पडला. या नकाशातील देशांच्या सीमा वस्तुस्थितीला धरून दाखवल्या असतीलच असे नाही.

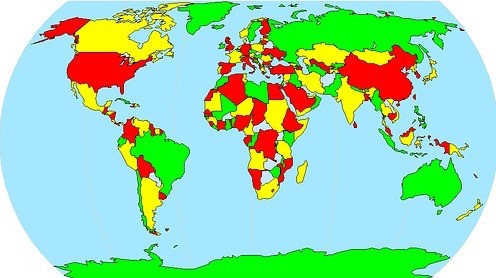
चार रंग वापरून उचित रीतीने रंगवलेला जगाचा जुना नकाशा

फ्रेडेरिक गथ्रीचे शिक्षक होते ऑगस्टस द मॉर्गन (Augustus De Morgan). त्यांनी २३ ऑक्टोबर १८५२ रोजी विल्यम हॅमिल्टन (William Hamilton) या गणितज्ञाला एक पत्र लिहिले, व नकाशा उचित रीतीने रंगवायचा म्हटला तर चार रंग नेहमीच पुरतील का अशी विचारणा केली. पाव शतकापेक्षा जास्त काळ लोटल्यावर १८७९ साली आल्फ्रेड ब्रे केम्प (Alfred Bray Kempe) या इंग्लिश गणितज्ञाने या प्रश्नाचे होकारार्थी उत्तर दिले, व ते ‘अमेरिकन जर्नल ऑफ मॅथेमॅटिक्स’मधील एका आठ पानी शोधनिबंधात प्रसिद्ध केले. त्याचे शीर्षक होते ‘चार रंगांच्या भौगोलिक प्रश्नाबाबत’ (On the geographical problem of the four colours).

आल्फ्रेड ब्रे केम्प

तब्बल अकरा वर्षे केम्पच्या युक्तिवादाबद्दल कोणी दुमत मांडले नाही. पण १८९० साली पर्सी जॉन हीवुड (Percy John Heawood) या इंग्लंडमधीलच गणितज्ञाने केम्पच्या उत्तरातील एक सूक्ष्म पण गंभीर चूक नजरेस आणली. मात्र केम्पच्याच काही संकल्पनांचा उपयोग करून हीवुडने सिद्ध केले की कुठलाही नकाशा उचित रीतीने रंगवण्यासाठी पाच रंग पुरेसे असतात. त्याला ‘पाच रंगांचे प्रमेय’ (Five Colour Theorem) असे नाव आहे. पण हीवुडने असा काही नकाशा शोधून काढला नव्हता की जो उचित रीतीने रंगवायला चार रंग पुरे पडत नाहीत. त्यामुळे तीन रंग पुरत नाहीत व पाच रंग पुरतात हे निश्चित झाले असले, तरी चार रंग नेहमी पुरतात की नाही हा प्रश्न अनिर्णितच राहिला. कुठलाही नकाशा उचित रीतीने रंगवण्यासाठी चार रंग पुरतील असा सर्वांचा कयास असल्यामुळे या विधानाला ‘चार रंगांचे अनुमान’ (Four Colour Conjecture) असे नाव देण्यात आले.

पर्सी जॉन हीवुड

१९७५ साली मी मुंबईच्या आय. आय. टी.तील गणित विभागात काम करू लागल्यानंतर पुढील वर्षी माझी पत्नी निर्मला मुंबई विद्यापीठातील गणित विभागात शिकवू लागली. तेथील एम. एस्सी.च्या दुसऱ्या वर्षातील विद्यार्थ्यांना आलेखशास्त्र (Graph Theory) हा ऐच्छिक विषय शिकता येत असे. विभागप्रमुख प्राध्यापक शरच्चंद्र श्रीखंडे यांच्या सूचनेनुसार डॉ. वासंती भट-नायकांनी हा विषय शिकवायला सुरुवात केली होती. मी निर्मलाला एकदा विचारले की हे विद्यार्थी हीवुडचा पाच रंगांचा सिद्धांत शिकतात का? ती म्हणाली की तो तर त्यांच्या पाठ्यक्रमाचा भागच आहे. मी उत्सुकता दाखवल्यावर तिने मला काही मूलभूत गोष्टी समजावून सांगितल्या. प्रथम नकाशा म्हणजे नेमके काय हे गणिती भाषेत सांगणे क्रमप्राप्त होते. पण ते जरा बाजूला ठेऊन, रंगकाम सुटसुटीत करण्यासाठी व मुख्यत्वे रंगकामातील निर्णय सुसूत्रपणे घेता यावेत म्हणून गणितज्ञांनी शोधून काढलेली एक युक्ति मला निर्मलाने सांगितली. नकाशात दाखवायच्या प्रत्येक वेगळ्या भूप्रदेशांत एक बिंदू निवडायचा व तो त्या प्रदेशाचा प्रतिनिधी आहे असे समजायचे. त्याचप्रमाणे सर्व भूप्रदेशांच्या बाहेरही एक बिंदू निवडायचा. हे भारताच्या प्रत्येक राज्याची राजधानी त्या राज्याचे प्रतिनिधित्व करते आणि भारतीय महासागरातील एका विशिष्ट ठिकाणी भारताची सागरीसत्ता केन्द्रित झाली आहे असे म्हणण्यासारखेच आहे. आता वेगवेगळ्या भूप्रदेशांना आणि त्या सर्वांच्या बाहेरच्या भागाला रंग देण्याऐवजी त्यांचे प्रतिनिधित्व करणाऱ्या बिंदूंनाच फक्त रंग द्यायचे. दोन प्रदेश एकमेकांना लागून आहेत हे दर्शवण्यासाठी त्यांचे प्रतिनिधित्व करणारे बिंदू एकमेकांना एका रेघेने जोडायचे, आणि अशा दोन बिंदूंना वेगळे रंग द्यायचे. बिंदूना जोडणाऱ्या रेघा एकमेकींना छेदून जात नाहीत अशी काळजीही घेता येते. अशा प्रकारे आपल्याला दिलेल्या नकाशाचे फक्त बिंदू आणि रेघा असलेल्या चित्रात रूपांतर करता येते. आकृती १ मधील पंचकोनी नकाशाचे असे रूपांतर खाली करून दाखवले आहे.

आकृती २

या मार्गाने पुढे जाण्यासाठी आपण आलेखशास्त्रातील काही मूलभूत कल्पना जाणून घेऊ या. एका कागदावर आपण काही बिंदू काढू या. त्यांपैकी कोणकोणते दोन बिंदू एकमेकांना जोडायचे ते आपणच ठरवायचे, आणि त्याप्रमाणे एक रेघ काढून ते दोन बिंदू जोडून टाकायचे. या रेघा सरळ असोत किंवा वाकड्या असोत, कोणते दोन बिंदू कुठल्या एका रेघेने जोडले जात आहेत हे नीट कळले म्हणजे झाले. मुद्दाम सांगायचे म्हणजे कुठल्याही बिंदूपासून त्याच्याचकडे जाणारी रेघ काढायची नाही आणि कुठल्याही दोन बिंदूंना एकापेक्षा जास्त रेघांनी जोडायचे नाही. अशा प्रकारे जे चित्र कागदावर तयार होते त्याला आलेख (graph) असे म्हणतात. त्यातील प्रत्येक बिंदूला ‘शिरोबिंदू’ (vertex) व प्रत्येक रेघेला ‘कडा’ (edge) अशी नावे आहेत. जे दोन शिरोबिंदू एकमेकांना (एका कडेने) जोडलेले असतात, त्यांना एकमेकांचे ‘शेजारी’ (neighbours) असे म्हणतात. एखाद्या शिरोबिंदूच्या शेजाऱ्यांची जी संख्या असते, तिला त्या शिरोबिंदूची कोटी (degree of a vertex) असे नाव आहे. दुसऱ्या शब्दात सांगायचे झाले तर, शिरोबिंदूची कोटी म्हणजे त्या शिरोबिंदूपासून निघणाऱ्या कडांची संख्या. काही उदाहरणे पाहू या. या आणि पुढील सर्व आकृतींत शिरोबिंदू • या चिह्नाने, व कडा ________ अशा सरळ किंवा एखाद्या वक्र रेघेने दाखवल्या आहेत.

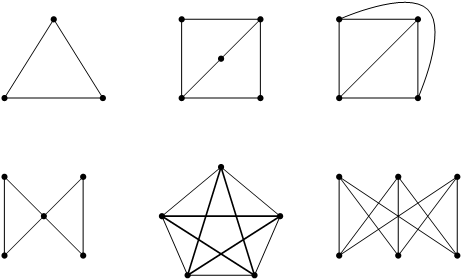
आकृती ३

वरील आलेखांपैकी पहिल्यात तीन शिरोबिंदू व तीन कडा आहेत, आणि प्रत्येक शिरोबिंदूची कोटी 2 आहे, कारण प्रत्येक शिरोबिंदूपासून 2 कडा निघतात. दुसऱ्या आलेखात पाच शिरोबिंदू व सहा कडा आहेत, आणि नैऋत्य व ईशान्य दिशेकडील दोन शिरोबिंदूची कोटी 3 आहे तर बाकीच्या तीन शिरोबिंदूची कोटी 2 आहे. तिसऱ्या आलेखात चार शिरोबिंदू व सहा कडा आहेत आणि प्रत्येक शिरोबिंदूची कोटी 3 आहे. चौथ्या आलेखात पाच शिरोबिंदू व सहा कडा आहेत, आणि मध्यवर्ती शिरोबिंदूची कोटी 4 आहे, तर बाकीच्या चार शिरोबिंदूंची कोटी 2 आहे. पाचव्या आलेखात पाच शिरोबिंदू व दहा कडा आहेत आणि प्रत्येक शिरोबिंदूची कोटी 4 आहे, तर सहाव्यात सहा शिरोबिंदू व नऊ कडा आहेत आणि प्रत्येक शिरोबिंदूची कोटी 3 आहे. पहिल्या, तिसऱ्या व पाचव्या आलेखात कुठलेही दोन शिरोबिंदू एकमेकांचे शेजारी आहेत, पण दुसऱ्या, चौथ्या व सहाव्या आलेखात मात्र तसे नाही.

जर एखाद्या आलेखातील कुठल्याही दोन कडा एकमेकींना छेदून जात नसतील, तर त्या आलेखाला प्रतल आलेख (plane graph) असे म्हणतात. (कडांचे एखाद्या शिरोबिंदूवर एकमेकींना मिळणे याला छेदून जाणे म्हणायचे नाही.) आकृती ३ मधील पहिले चार आलेख प्रतल आहेत, पण शेवटचे दोन आलेख प्रतल नाहीत कारण त्या दोन्ही आलेखात एकमेकींना छेदून जाणाऱ्या कडा आहेत. आपल्याकडे एखादा नकाशा असेल, व त्याच्यातील प्रदेशांचे बिंदुरूपी प्रतिनिधी निवडून आणि लगतच्या दोन प्रदेशांच्या प्रतिनिधींना एका रेघेने जोडून मिळणारा आलेख प्रतल असतो, कारण अशा दोन रेघा एकमेकींना छेदणार नाहीत अशी काळजी घ्यायची असते. यामुळे आपण यापुढे फक्त प्रतल आलेखांचाच विचार करणार आहोत. लिओनार्ड ऑयलर (Leonhard Euler) या स्विस गणितज्ञाने १७५८ साली दिलेले एक सूत्र (formula) वापरून असे सिद्ध करता येते की प्रत्येक प्रतल आलेखात एक तरी शिरोबिंदू असा असतो की ज्याची कोटी जास्तीत जास्त 5 आहे. हे प्रमेय आपल्याला खूप उपयोगी ठरणार आहे.

आता चार रंगांच्या नकाशाचा प्रश्न असा मांडता येईल. समजा आपल्याकडे एक प्रतल आलेख आहे, व त्यातील शिरोबिंदू असे रंगवायचे आहेत की जर दोन शिरोबिंदू एकमेकांचे शेजारी असतील तर त्यांना वेगळे रंग दिले जातील. शिरोबिंदू असे रंगवण्याला ‘उचित रीतीने’ रंगवणे असे म्हणू या. शिरोबिंदूंच्या उचित रंगकामासाठी नेहमीच चारच रंग जर पुरत असतील, तर कुठलाही नकाशा उचित रीतीने रंगवण्यासाठी चार रंग पुरेसे असतात असे सिद्ध होईल. आपल्या प्रश्नाच्या या नव्या मांडणीत नकाशातील प्रदेशांच्या सीमा एकमेकींना कशा भिडतात किंवा एखाद्या प्रदेशाला समुद्रकिनारा आहे का नाही, हे मुद्दे उपस्थित होत नाहीत. शिवाय आपल्याला या प्रश्नाचा विचार आलेखशास्त्रातील सर्वमान्य प्रमेये व नेहमीच्या रचना वापरून करता येतो.

गणितातील काही प्रमेयांची सिद्धता विसंगती दाखवून करता येते, म्हणजे एखादे विधान खरे आहे असे सिद्ध करायचे असेल तर क्षणभर ते विधान खोटे आहे असे मानायचे. त्यामुळे काही विसंगती निर्माण होते असे जर दाखवता आले, तर दिलेले विधान खरे आहे असे आपोआप सिद्ध होते, कारण निर्माण झालेली विसंगती टाळण्याचा एकच उपाय आहे, व तो म्हणजे विधानाची सत्यता मानणे! अशा सिद्धतेला विरोधजन्य सिद्धता (proof by contradiction) असे म्हणता येईल. या पद्धतीनुसार, ‘प्रतल आलेखातील शिरोबिंदू उचित रीतीने रंगवण्यासाठी चार रंग पुरतात’ हे विधान खोटे आहे असे क्षणभर मानू या. म्हणजे एकतरी प्रतल आलेख असा असणार की ज्याचे शिरोबिंदू उचित रीतीने रंगवण्यासाठी चार रंग पुरत नाहीत. अशा प्रतल आलेखाला प्रत्युदाहरण (counterexample) असे म्हणतात. या प्रत्युदाहरणांपैकी ज्या आलेखात सर्वात कमी शिरोबिंदू असतील अशा कुठल्याही प्रत्युदाहरणाला किमान स्वरूपाचे प्रत्युदाहरण (minimal counterexample) असे म्हणतात. जर आपण असे दाखवले की किमान स्वरूपाच्या प्रत्युदाहरणामुळे विसंगती निर्माण होते, तर ते अस्तित्वात असू शकणार नाही, व म्हणून कुठलेही प्रत्युदाहरण अस्तित्वात असू शकणार नाही, आणि परिणामतः ‘प्रतल आलेखातील शिरोबिंदू उचित रीतीने रंगवण्यासाठी चार रंग पुरतात’ हे विधान सिद्ध होईल.

समजा आपल्याकडे किमान स्वरूपाचे एक प्रत्युदाहरण आहे. त्या आलेखाला आपण A असे नाव देऊ या, व त्यातील शिरोबिंदूंची संख्या n आहे असे समजू या. हे प्रत्युदाहरण किमान स्वरूपाचे असल्याने n पेक्षा कमी शिरोबिंदू असलेल्या कुठल्याही प्रतल आलेखातील शिरोबिंदू उचित रीतीने रंगवण्यासाठी चार रंग निश्चित पुरणार. जर n = 100 असेल, तर याचा अर्थ असा होतो की 1 ते 99 पर्यंत कितीही शिरोबिंदू असलेला प्रतल आलेख प्रत्युदाहण होऊ शकत नाही, म्हणजे त्याचे शिरोबिंदू उचित रीतीने रंगवण्यासाठी चार रंग पुरतात. आता A या आलेखातील एक शिरोबिंदू (व त्याबरोबर त्याच्या पासून निघणाऱ्या सर्व कडा) वगळू या. उरलेल्या आलेखात n - 1 शिरोबिंदू आहेत; ते n पेक्षा कमी आहेत, व म्हणून जास्तीत जास्त चार रंग वापरून ते आपण उचित रीतीने रंगवू या. समजा वगळलेल्या शिरोबिंदूची कोटी जास्तीत जास्त 3 आहे, म्हणजे A या आलेखात त्याचे जास्तीत जास्त 3 शेजारी आहेत. मग या शेजाऱ्यांना आता जे काही रंग मिळाले असतील ते सोडून चार रंगांपैकी उरलेला रंग आपण वगळलेल्या शिरोबिंदूला देऊ शकतो, आणि त्याचा A या आलेखात (वगळलेल्या कडांसह) परत समावेश करू शकतो. अशाप्रकारे A या आलेखाचे सर्व शिरोबिंदू चार रंग वापरून उचित रीतीने रंगवले जातात. पण A हा आलेख एक प्रत्युदाहरण असल्याने त्याच्या बाबतीत असे करणे शक्य नसते. अशी विसंगती निर्माण होते. याचा अर्थ असा होतो की कुठल्याही किमान स्वरूपाच्या प्रत्युदाहरणात 3 किंवा 3 पेक्षा कमी कोटीचे शिरोबिंदू असूच शकत नाहीत.

आता समजा की A या आलेखातून वगळलेल्या शिरोबिंदूची कोटी 4 आहे. मग वरील युक्तिवाद करता येणार नाही, कारण वगळलेल्या शिरोबिंदूच्या 4 शेजाऱ्यांना रंगवण्यात चार रंग संपून गेले असले तर वगळलेल्या शिरोबिंदूचा परत समावेश करताना त्याच्यासाठी पाचवा रंग वापरावा लागेल. ही परिस्थिती हाताळण्यासाठी केम्प या गणितज्ञाने १८७९ मध्ये ‘एक-आड-एक रंगवलेल्या शिरोबिंदूंची साखळी’ (chain of alternately coloured vertices) ही संकल्पना प्रस्तुत केली. नंतर ती ‘केम्प साखळी’ (Kempe chain) या नावाने ओळखली जाऊ लागली. वगळलेल्या शिरोबिंदूची कोटी 4 असेल तर उरलेल्या शिरोबिंदूंपैकी एका विशिष्ट साखळीतील शिरोबिंदूंच्या दोन रंगाची अदलाबदल अशी करता येते की वगळलेल्या शिरोबिंदूच्या शेजाऱ्यांना तीनच रंग मिळतात, व म्हणून त्याचा परत समावेश करताना पाचवा रंग वापरावा लागत नाही असे केम्पने दाखवले. त्यामुळे पुन्हा विसंगती निर्माण होते. याचा अर्थ असा झाला की कुठल्याही किमान स्वरूपाच्या प्रत्युदाहरणात ४ कोटीचा शिरोबिंदूही असू शकत नाही.

A या आलेखातून वगळलेल्या शिरोबिंदूची कोटी 5 असेल तर अशीच विसंगती निर्माण होते हे दाखवण्याचा केम्पने प्रयत्न केला. या प्रयत्नात त्याने एकाच वेळी दोन विशिष्ट साखळींमधील शिरोबिंदूंच्या दोन रंगाची अदलाबदल केली होती. परंतु असे करणे अयोग्य आहे, हे हीवुड या गणितज्ञाने एका उदाहरणासह दाखवून दिले. त्यामुळे या बाबतीतला केम्पचा युक्तिवाद सदोष ठरला. तो जर निर्दोष असता, तर कुठल्याही किमान स्वरूपाच्या प्रत्युदाहरणात 5 कोटीचा शिरोबिंदूदेखील असू शकत नाही असे ठरले असते. पण आपण आधी पाहिल्याप्रमाणे प्रत्येक प्रतल आलेखात एकतरी शिरोबिंदू असा असतो की ज्याची कोटी जास्तीत जास्त 5 आहे.
त्यामुळे किमान स्वरूपाचे प्रत्युदाहरणच असू शकत नाही, व पर्यायाने कुठलाही प्रतल आलेख प्रत्युदाहरण असू शकत नाही, म्हणजेच प्रत्येक प्रतल आलेख उचित रीतीने रंगवण्यास चार रंग पुरतात असे सिद्ध झाले असते. पण तसे झाले नाही.

केम्पची सिद्धता 5 कोटीचा शिरोबिंदू वगळण्याबाबत फसली असली तरी सगळेच मुसळ काही केरात गेले नव्हते. एक तर चार रंग वापरून प्रतल आलेख उचित रीतीने रंगवताना कुठल्याही किमान स्वरूपाच्या प्रत्युदाहरणात 1, 2, 3 किंवा 4 कोटीचे शिरोबिंदू असू शकत नाहीत, म्हणजे त्यातील सर्व शिरोबिंदू 5 किंवा 5 पेक्षा जास्त कोटीचे असले पाहिजेत हे सिद्ध झाले होते.

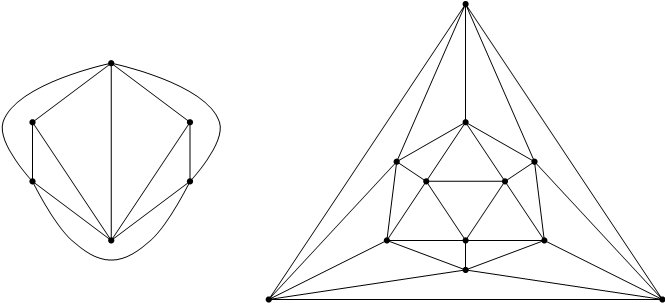
आकृती ४ (अ) - डावीकडे व आकृती ४ (ब) - उजवीकडे

डावीकडील आकृती ४ (अ) मधील आलेखात दोन शिरोबिंदू 3 कोटीचे, दोन शिरोबिंदू 4 कोटीचे आणि दोन शिरोबिंदू 5 कोटीचे आहेत. या आलेखात 5 पेक्षा कमी कोटीचे शिरोबिंदू असल्याने व त्यापैकी कुठलाही एक शिरोबिंदू वगळता येत असल्याने हा आलेख कुठल्याही किमान स्वरूपाच्या प्रत्युदाहरणाचा भाग होऊ शकत नाही. मात्र उजवीकडील आकृती ४ (ब) मध्ये विंशफलकाच्या (icosahedron) आलेखातील सगळे बारा शिरोबिंदू 5 कोटीचे आहेत, व म्हणून कोणताच शिरोबिंदू वगळून केम्पचे तंत्र वापरता येत नाही. अशा आलेखांसाठी काही वेगळा मार्ग काढणे जरूर होते.

आता समजा आपल्याला चारच्या ऐवजी पाच रंग वापरायची परवानगी आहे. प्रतल आलेख चार रंग वापरून उचित रीतीने रंगवायचा असेल तर कुठल्याही किमान स्वरूपाच्या प्रत्युदाहरणात 4 कोटीचा शिरोबिंदू असू शकत नाही हे दाखवण्यासाठी केम्पने जो युक्तिवाद केला होता, त्याच युक्तिवादाने असे दाखवता येते की जर प्रतल आलेख पाच रंग वापरून उचित रीतीने रंगवायचा असेल तर कुठल्याही किमान स्वरूपाच्या प्रत्युदाहरणात 5 कोटीचा शिरोबिंदू असू शकत नाही. त्यामुळे अशा प्रत्युदाहरणात 1 ते 5 यांपैकी कुठल्याच कोटीचा शिरोबिंदू असू शकत नाही. पण आपण आधीच पाहिले आहे की ऑयलरच्या सूत्रानुसार प्रत्येक प्रतल आलेखात 1 ते 5 यांपैकी कुठल्या तरी कोटीचा शिरोबिंदू असलाच पाहिजे. याचा अर्थ की प्रतल आलेखाचे पाच रंग वापरून उचित रीतीने रंगकाम करायचे असेल, तर किमान स्वरूपाचे प्रत्युदाहरण असूच शकत नाही, व त्यामुळे कोणतेही प्रत्युदाहरण होऊ शकत नाही, कारण जर एखादा प्रतल आलेख प्रत्युदाहरण असेल, तर अशा प्रत्युदाहरणांपैकी एकात तरी कमीत कमी शिरोबिंदू असणारच, व तो आलेख किमान स्वरूपाचे प्रत्युदाहरण बनेल. हे नेहमीच्या शब्दात सांगायचे झाले तर कुठलाही प्रतल आलेख पाच रंग वापरून उचित रीतीने रंगवता येतो असे सिद्ध होते. ही निष्पत्ती १८९० सालीच हीवुडने प्रस्तुत केली होती. कालांतराने हे पाच रंगांचे प्रमेय जगभरात शिकवल्या जाणाऱ्या आलेखशास्त्राच्या पाठ्यक्रमात अंतर्भूत झाले. निर्मला मुंबई विद्यापीठाच्या ज्या गणित विभागात शिकवत होती तेथेही हाच प्रघात होता. पण ही परिस्थिती सुधारण्याची चिह्ने दिसत होती. ती कशी सुधारली याची कहाणी पुढच्या लेखात.

(पुढील भाग इथे)
---

बालमोहन लिमये

(balmohan.limaye@gmail.com)



लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.

बालमोहन लिमये यांचे इतर लिखाण