बीबरबाखचे अनुमान
बीबरबाखचे अनुमान
बालमोहन लिमये
(‘गणिताच्या निमित्ताने' ही १२ भागांची लेखमाला तीन आठवड्यांपूर्वी संपली. बालमोहन लिमये यांचे त्याच धर्तीवरील आणखी काही लिखाण क्रमशः प्रकाशित करत आहोत.)
संमिश्र विश्लेषण (Complex Analysis) ही गणिताची एक महत्त्वपूर्ण शाखा आहे. तिच्यात संमिश्र संख्यांचा (complex numbers) वापर सर्रास होत असल्याने तिला हे नाव मिळाले आहे. ‘संख्यांच्या दुनियेत’ या लेखात (इथे पहा) आपण संमिश्र संख्यांची तोंडओळख करून घेतली, आणि त्यांची व्याप्ती जाणून घेतली. संमिश्र विश्लेषणातील काही अनुमाने जगभरातील गणितज्ञांना कित्येक दशके किंवा शतके हुलकावणी देत राहिली होती. त्यांपैकी वर्णन करायला त्यातल्या त्यात सोप्या असणाऱ्या मोजक्या अनुमानांपैकी एक आहे बीबरबाखचे अनुमान (Bieberbach Conjecture). ‘गणिताच्या निमित्ताने’ या लेखमालेच्या नवव्या भागात (इथे पहा) या अनुमानाचा उल्लेख आला होता.
फलन (function) ही गणितातील, आणि विशेषतः संमिश्र विश्लेषणातील, सर्वात मूलभूत संकल्पना आहे. समजा आपल्याकडे संमिश्र संख्यांचा एक संच आहे; त्याला D असे नाव देऊ या. जर z ही D मधील एक संमिश्र संख्या असेल, तर तिचा आपण एका w या विशिष्ट संमिश्र संख्येशी संबंध लावायचे ठरवू या. ही नवी संख्या z या दिलेल्या संख्येवर अवलंबून असल्याचे दर्शविण्यासाठी w = f(z) असे लिहू या. अशाप्रकारे D या अधिक्षेत्रावर (domain) f हे फलन सुनिश्चित होते; f(z) ही संख्या म्हणजे f ह्या फलनाने z या संख्येला दिलेली किंमत (value) आहे असे म्हटले जाते. या प्रक्रियेकडे आपण z ही आगत संख्या (input) आणि f(z) ही निर्गत संख्या (output) याप्रकारेही बघू शकतो.
एक उदाहरण बघू या. ज्या संमिश्र संख्यांचे केवल मूल्य (absolute value) 1 पेक्षा कमी आहे अशा संख्यांच्या संचाला विवृत एककी चकती असे म्हणतात. समजा ही चकती आपला संच D आहे. आपण z ह्या D मधील कुठल्याही संमिश्र संख्येचा w = f(z) = z2 असा संबंध निश्चित केला, तर f या फलनाने z = ½ या संख्येला दिलेली किंमत f(½) = ¼ आहे, तर z = ⅓ या संख्येला दिलेली किंमत f(⅓) = 1/9 आहे. आपण दुसरा एक संबंध w = g(z) = 1/(1 – z) असा निश्चित केला, तर g या फलनाने z = ½ या संख्येला दिलेली किंमत g(½) = 2 आहे, तर z = ⅓ या संख्येला दिलेली किंमत g(⅓) = 3/2 आहे.
जर एखादे फलन D मधील भिन्न संख्यांना भिन्न किंमती देत असेल, तर ते फलन एकास-एक (one-one) आहे असे म्हणतात. वर w = f(z) = z2 या सूत्राने दिलेले फलन एकास-एक नाही, कारण f(½) = ¼ = f(-½), म्हणजे ½ आणि -½ या भिन्न संख्यांना ते ¼ ही समान किंमत देते. मात्र वर w = g(z) = 1/(1 – z) या सूत्राने दिलेले फलन एकास-एक आहे, कारण जर z1 आणि z2 या D मधील भिन्न संख्या असल्या, तर 1 - z1 आणि 1 - z2 यादेखील भिन्न संख्या असतात, व म्हणून g(z1) = 1/(1 – z1) आणि g(z2) = 1/(1 – z2) या संख्यासुद्धा भिन्न असतात, म्हणजे g हे फलन D मधील भिन्न संख्यांना भिन्न किंमती देते. बीबरबाखचे अनुमान एकास-एक असणाऱ्या फलनांसंबंधी आहे.
समजा n ही एक नैसर्गिक संख्या आहे, आणि a0, a1, a2, …, an या संमिश्र संख्या आहेत. आता z ही कुठलीही संमिश्र संख्या असेल, तर आपल्याला माहीत असलेल्या संमिश्र संख्यांच्या बेरीज व गुणाकार या क्रिया पुन्हा पुन्हा वापरून a0 + a1 z + a2 z2 + … + an zn अशी बहुपदी (polynomial) बनवता येते; येथील a0, a1, a2,…, an या संमिश्र संख्यांना या बहुपदीचे सहगुणक (coefficients) असे म्हणतात. खरे म्हणजे इथे आपण
असे एक फलन सुनिश्चित केले आहे, z या कोणत्याही संमिश्र संख्येसाठी.
खूपदा गणितज्ञांना अनंताची ओढ असते, म्हणजे एखादी क्रिया सतत करत राहिलो आणि कधी थांबलोच नाही, तर काय होईल हे शोधून काढण्याचे कुतूहल असते. समजा आपल्याकडे a0, a1, a2, … अशा अनंत संमिश्र संख्या आहेत. वर दिलेल्या बहुपदीत आपण an+1 zn+1, an+2 zn+2, … अशी पदे मिळवत राहिलो, तर आपल्याला Σ an zn अशी एक घातश्रेणी (power series) मिळते; येथील a0, a1, a2,…, an,… या संमिश्र संख्यांना घातश्रेणीचे सहगुणक असे म्हणतात. पण अनंत वेळा पदे मिळवत रहाणे याचा अर्थ काय असा प्रश्न उभा राहतो. त्याचे उत्तर देण्याचा प्रयत्न करतो. जर z ही एक संमिश्र संख्या दिली असेल, आणि वरील बहुपदीत आणखी पदे मिळवत राहिल्याने आपण w या एका विशिष्ट संमिश्र संख्येपर्यंत पोचत असू, म्हणजे ती बहुपदी आणि w यांतील अंतर शून्याकडे जात असेल, तर Σ an zn ही घातश्रेणी z ह्या संमिश्र संख्येसाठी अभिसारणी (convergent) आहे, व w ही तिची बेरीज (sum) आहे असे म्हणायचे, आणि Σ anzn = w असे लिहायचे; इथे घातश्रेणीची बेरीज असलेली w ही संमिश्र संख्या z या संमिश्र संख्येवर अवलंबून असल्याने w = f(z) असे, म्हणजेच f(z) = Σ an zn असे, एक फलन सुनिश्चित होते. अशा वेळी Σ an zn ही घातश्रेणी f या फलनाला प्रतिरूपित करते (represent) असेही म्हणतात.
एका सोप्या घातश्रेणीचे उदाहरण पाहू या. समजा a0 = 0, आणि a1, a2,…, an,... हे सगळे सहगुणक समान असून ते 1 च्या बरोबर आहेत, म्हणजे a1 = 1, a2 = 1,…, an = 1,… वगैरे. मग n ह्या नैसर्गिक संख्येसाठी आपली बहुपदी z + z2 + … + zn अशी होते. पण
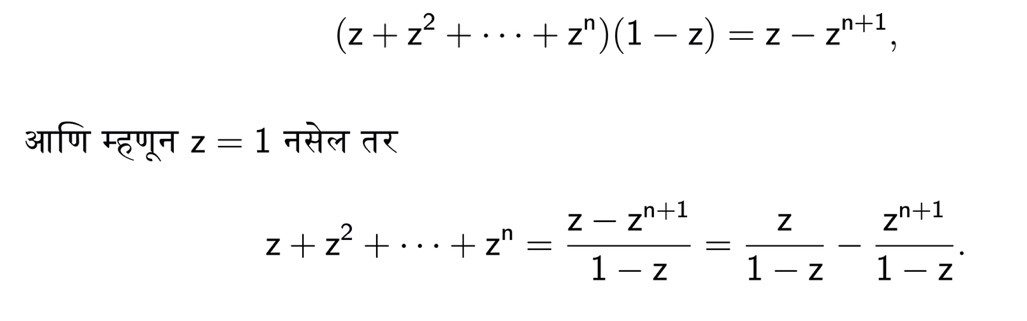
आता समजू या की ।z। < 1, म्हणजे z हा बिंदू विवृत एककी चकतीमध्ये आहे, आणि w = z / (1 – z). मग जसजसा n वाढत जाईल तसतशी ।z।n+1 ही वास्तव संख्या लहान होत जाणार, म्हणजे आपण जसजशी जास्त पदे मिळवत जाऊ, तसतसे w – (z + z2 + … + zn) ह्या वजाबाकीचे केवल मूल्य कमी होत जाणार आणि शून्याकडे जाणार. उदाहरणार्थ, z = ½ असेल, तर 1 / (1 – z) = 2, आणि वरील वजाबाकीचे केवल मूल्य n = 1, 2, 3, 4 यांसाठी 1/2, 1/4, 1/8, 1/16 असे कमीकमी होत जाते. तसेच z = -½ असेल, तर
1 / (1 – z) = 2/3, आणि वरील वजाबाकीचे केवल मूल्य n = 1, 2, 3, 4 यांसाठी 1/6, 1/12, 1/24, 1/48 असे कमीकमी होत जाते. यावरून असे कळून येते की ।z। < 1 असेल, तर z + z2 + z3 + … + zn + … ही घातश्रेणी अभिसारणी आहे, आणि तिची बेरीज w = z / (1 – z) आहे. याचा अर्थ असा होतो की विवृत एककी चकतीमधील z या बिंदूसाठी f(z) = z / (1 – z) अशी एका फलनाची व्याख्या केली, तर z + z2 + z3 + … + zn + … ही घातश्रेणी f या फलनाला प्रतिरूपित करते. उदाहरणार्थ, z = ½, असेल तर या घातश्रेणीची बेरीज f(½) = 1 होते, तर z = –½, असेल तर या घातश्रेणीची बेरीज f(-½) = -⅓ होते. आपण z = 1, 2, –1, किंवा –2 घालू शकत नाही, कारण या संख्यांचे केवल मूल्य 1 पेक्षा कमी नाही, व म्हणून त्या विवृत एककी चकतीमध्ये नाहीत.
आता समजू या की a0 = 0 आणि a1 = 1, पण a2, a3,…, an, … ह्या कोणत्याही संमिश्र संख्या आहेत. असेही मानू या की z ह्या विवृत एककी चकतीमधील कुठल्याही बिंदूसाठी z + a2 z2 + a3 z3 + … + an zn + … ही घातश्रेणी अभिसारणी आहे, व ती ज्या फलनाला प्रतिरूपित करते ते फलन एकास-एक आहे, म्हणजे ते विवृत एककी चकतीमधील भिन्न बिंदूंना भिन्न किंमती देते. लुडविग बीबरबाख (Ludwig Bieberbach) या जर्मन गणितज्ञाने १९१६ साली असे सिद्ध केले की या प्रकारच्या कुठल्याही घातश्रेणीमध्ये ।a2। ≤ 2, म्हणजे a2 या सहगुणकाचे केवल मूल्य जास्तीत जास्त 2 असू शकते. आपल्या सिद्धतेमधील एका तळटीपेत (footnote) त्याने असे अनुमान केले की ।a3। ≤ 3, ।a4। ≤ 4, … वगैरे, याचा अर्थ असा की n ही कुठलीही नैसर्गिक संख्या असेल तर ।an। ≤ n, म्हणजे an या सहगुणकाचे केवल मूल्य जास्तीत जास्त n असू शकते.

बीबरबाखच्या शोधनिबंधाचा मथळा आणि त्याच्यातील तळटीप
आता कोणी असे म्हणेल की z + 4z2 + 4z3 या घातश्रेणीचे जे सहगुणक आहेत, म्हणजे a2 = 4, a3 = 4, a4 = 0, a5 = 0, …, an = 0,… ते तर बीबरबाखचे अनुमान पाळत नाहीत, कारण ।a2। > 2 आणि ।a3। > 3. तर त्याचे उत्तर असे आहे की ही घातश्रेणी प्रतिरूपित करत असलेले f(z) = z + 4z2 + 4z3 हे फलन एकास-एक नाही, कारण f(0) = 0 = f(–½), आणि म्हणून या घातश्रेणीबद्दल बीबरबाखने अनुमान बांधलेलेच नाही. ज्या प्रकारच्या घातश्रेणींबद्दल बीबरबाखने अनुमान बांधले आहे, त्यांची तीन प्रमुख उदाहरणे अशी आहेत :
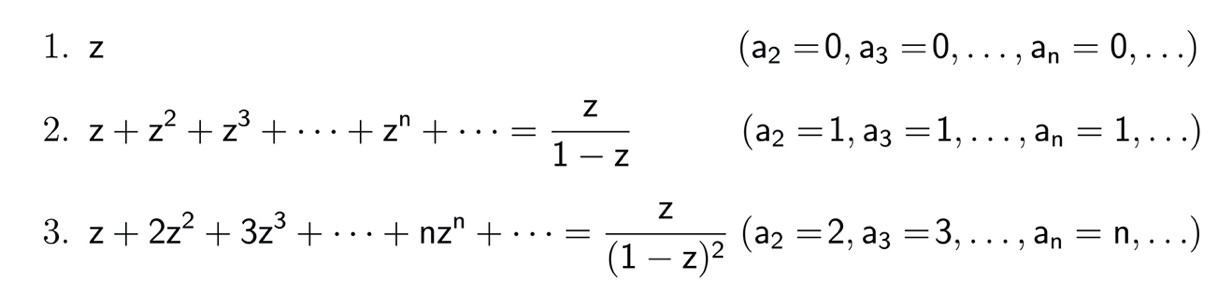
यांपैकी पहिल्या उदाहरणातील घातश्रेणीचे दुसऱ्या सहगुणकापासून सर्व सहगुणक शून्य आहेत, म्हणजे त्यांचे केवल मूल्य (absolute value) सर्वात कमी आहे. तिसऱ्या उदाहरणांतील घातश्रेणी जे फलन प्रतिरूपित करते त्याला कोबे फलन (Koebe function) असे म्हणतात. बीबरबाखच्या अनुमानाचा रोख असा आहे की या तिसऱ्या उदाहरणातील घातश्रेणीचे जे सहगुणक आहेत, त्यांपेक्षा कुठल्याही घातश्रेणीच्या सहगुणकांचे केवल मूल्य जास्त असता कामा नये. याचा अर्थ असा की ज्या घातश्रेणींबद्दल बीबरबाखने अनुमान बांधले त्या सगळ्या घातश्रेणींचे सहगुणक पहिल्या व तिसऱ्या उदाहरणांतील सहगुणकांच्या कुठे तरी मध्ये असले पाहिजेत, जसे दुसऱ्या उदाहरणातील घातश्रेणीचे आहेत. या दुसऱ्या उदाहरणातल्या घातश्रेणीला भूमितीय घातश्रेणी (geometric series) असे म्हणतात. तिचा विचार आपण आधीच केला आहे.
बीबरबाखने फक्त ।a2। ≤ 2 असे सिद्ध केल्याने त्याची गाडी दुसऱ्या सहगुणकापाशी, म्हणजे n = 2 पाशी, थांबली. त्यानंतर सात वर्षांनी म्हणजे १९२३ साली चार्ल्स ल्यूव्नर (Charles Löwner) या अमेरिकन गणितज्ञाने तिसऱ्या सहगुणकाबद्दल ।a3। ≤ 3 असे सिद्ध करून गाडी n = 3 पाशी आणली. त्यावेळी बीबरबाखने ल्यूव्नरबरोबर हस्तांदोलन केले, व तो ल्यूव्नरला म्हणाला की तुझ्या पुढच्या शोधनिबंधात उरलेल्या सर्व सहगुणकांचा तू समाचार घेशील. पण तसे काही झाले नाही. सुमारे बत्तीस वर्षांनी म्हणजे १९५५ साली गाराबेडिअन (Garabedian) व शिफर (Schiffer) यांनी ।a4। ≤ 4, आणि आणखी तेरा वर्षांनी म्हणजे १९६८ साली पीडरसन (Pederson) याने व स्वतंत्रपणे ओझावा (Ozawa) याने ।a6। ≤ 6 असे सिद्ध केले. पाचव्या सहगुणकाबद्दल ।a5। ≤ 5 असे सिद्ध व्हायला अजून चार वर्षे लागली, व ते काम पीडरसन व शिफर यांनी केले.
मध्यंतरीच्या काळात काही खास प्रकारच्या घातश्रेणींसाठी बीबरबाखचे अनुमान खरे असल्याचे दाखवण्यात आले. उदाहरणार्थ, १९३१–१९३२ मध्ये द्युदोने (Dieudonne) व रोगोसिन्स्की (Rogosinski) यांनी जर a2, a3,…, an, … हे सगळे सहगुणक वास्तव (real) असले, तर बीबरबाखचे अनुमान खरे असल्याचे दाखवले. १९७२ साली कार्ल फिट्स्जेरल्ड (Carl Fitzgerald) या गणितज्ञाने n ही कुठलीही नैसर्गिक संख्या असेल तर ।an। < (7/6)½n असे सिद्ध केले. आता (7/6)½ ही संख्या 1 पेक्षा फक्त 0.0802 एवढीच जास्त आहे, पण गणितज्ञांचे समाधान झाले नाही. त्यांना ।an। ≤ n असेच सिद्ध करायचे होते. रॉबर्टसन आणि मिलिन या गणितज्ञांनी १९६५ साली काही जास्त व्यापक अनुमाने सुचवली, जी सिद्ध केली तर बीबरबाखचे अनुमान आपोआप सिद्ध व्हावे अशी. पण ती अनुमाने त्यांना किंवा इतर कुणालाही सिद्ध करता आली नव्हती. थोडक्यात, १९८४ सालापर्यंत बीबरबाखच्या अनुमानाची गाडी n = 6 पाशीच थांबून राहिली.
अमेरिकेतील पर्ड्यू विद्यापीठाच्या गणित विभागात १९६२ सालापासून लुई द ब्रान्ज (Louis de Branges) हे प्राध्यापक काम करू लागले होते. त्यांच्या संशोधनाचे मुख्य प्रांत ऑपरेटर थिअरी (Operator Theory) व स्पेशल फंक्शन्स (Special Functions) हे होते. तरीही १९७७ सालापासून त्यांनी बीबरबाखच्या अनुमानावर लक्ष केन्द्रित केले होते. आपण तज्ज्ञ असलेल्या प्रांतांतील संकल्पना वापरून जानेवारी १९८४ अखेर ते बीबरबाखचे अनुमान सिद्ध करण्याच्या अगदी जवळ येऊन ठेपले होते. त्यांच्या मते n ही दोन किंवा त्यापेक्षा मोठी नैसर्गिक संख्या असेल तर ।an। ≤ n असे सिद्ध करण्यासाठी काही n – 2 विशिष्ट बहुपदींचे मूल्य (0,1) या विवृत अंतरालातील (open interval) बिंदूंसाठी नेहमी धन (positive) असते हे दाखवले की काम भागणार होते. जर n = 3 असेल, तर ही बहुपदी होती 2(1 - x), व त्यामुळे काही प्रश्नच नव्हता. द ब्रान्ज यांनी कागद-पेन्सिल वापरून n = 4, 5 व 6 या संख्यांबद्दलच्या बहुपदींचे मूल्य (0,1) मधील बिंदूंसाठी धन असल्याचे दाखवलेही. पण त्यांतून नवीन काहीच निष्पन्न झाले नाही कारण ।a2। ≤ 2, ।a3। ≤ 3, ।a4। ≤ 4, ।a5। ≤ 5 व ।a6। ≤ 6 यांची सिद्धता इतरांनी आधीच वेगळ्या प्रकारे दिली होती. शेवटी द ब्रान्ज यांनी त्यांच्याच विभागात काम करणाऱ्या वॉल्टर गॉस्की (Walter Gautschi) या प्राध्यापकांना संगणक वापरून n = 7 पासून पुढे लागणाऱ्या बहुपदींची मूल्ये धन आहेत का हे पहाण्याची विनंती केली. सुरुवातीला इतर अंगीकृत कामांमुळे आणखी एक प्रकल्प पत्करायला गॉस्की तयार नव्हते, पण द ब्रान्ज यांच्या एका सेमिनारला उपस्थित राहिल्यानंतर या कामाने बीबरबाखचे अनुमान सिद्ध करता येणार आहे हे गॉस्कींच्या लक्षात आले. त्यांनी आपली इतर कामे बाजूला ठेवली. पर्ड्यू विद्यापीठातील CDC 6500 या संगणकाच्या साह्याने एका आठवड्याच्या आत गॉस्कींनी n = 30 पर्यंत मजल मारली. ही गोष्ट फारच समाधानकारक होती, कारण ।a7। ≤ 7 पासून ते ।a30। ≤ 30 या सगळ्यांच्या सिद्धता पदरात पडणार होत्या. द ब्रान्ज यांना फारच हुरूप आला. संगणकासाठी लिहिलेला प्रोग्रॅम सुधारल्यावर गॉस्कींच्या अपेक्षा आणखी उंचावल्या.
परंतु संगणकाच्या साह्याने हे काम पूर्ण होणे अशक्य होते, कारण नैसर्गिक संख्या अनंत आहेत, व एकेक करून संगणक त्या सर्व संपवू शकत नाही! शिवाय दर मोठ्या संख्येसाठी संगणक वापरण्याची किंमतही वाढत जात होती. म्हणून गॉस्कींच्या मनात आले की त्या विशिष्ट बहुपदींच्या धनतेसंबंधीचा (positivity) प्रश्न कदाचित कुणी विश्लेषण पद्धतीने (analytical method) आधीच हाताळला असला तर सोन्याहून पिवळे होईल. त्यांना ही शक्यता फारच दूरची वाटत होती. तरीही चौकशी तर करावी म्हणून त्यांनी असे प्रश्न हाताळणाऱ्या एका मित्राला फोन लावला. त्यांचे नाव होते रिचर्ड ॲस्की (Richard Askey). ते विस्कॉन्सिन विद्यापीठाच्या (University of Wisconsin) गणित विभागात काम करत. गॉस्कींचा प्रश्न व त्याचे अपेक्षित परिणाम ऐकल्याबरोबर ॲस्की उद्गारले, ‘पूर्णतः हास्यास्पद!’ (preposterous!). मग आपला प्रश्न विचारात घेण्यासाठी गॉस्कींना ॲस्कींची मनधरणी करावी लागली. त्याच दिवशी रात्री गॉस्कींचा फोन खणखणला. फोनवर होते ॲस्की. ते म्हणाले की आठ वर्षांपूर्वी त्यांनी व जॉर्ज गॅस्पर (George Gasper) या दोघांनी सिद्ध केलेल्या एका प्रमेयाद्वारे त्या विशिष्ट बहुपदींच्या धनतेची खात्री देता येते, आणि या गोष्टीचे त्यांना स्वतःलाच आश्चर्य वाटून राहिले आहे. गॉस्की चाट झाले. त्यांना आता संगणकाचे काही देणे-घेणे राहिले नव्हते. सर्वात खूष झाले ते द ब्रान्ज. अडुसष्ट वर्षे दाद न देणारे एक ख्यातनाम अनुमान त्यांच्या दृष्टीने सिद्ध झाले होते.
द ब्रान्ज यांनी हा शोध लिहून काढला व आपण लिहीत असलेल्या पुस्तकातील सहा प्रकरणांपैकी शेवटचे प्रकरण म्हणून त्याचा समावेश केला. त्यांनी त्या पुस्तकाचे 385 पानी हस्तलिखित (manuscript) बारा-चौदा तज्ज्ञांकडे तपासून पाहण्यासाठी पाठवले. त्यांपैकी प्रत्येकाने एकेक छान कारण सांगून आपल्याला बीबरबाखच्या अनुमानाची सिद्धता तपासून पहाणे का शक्य नाही ते कळवले! द ब्रान्ज खट्टू झाले. याच सुमारास त्यांना अमेरिका व रशिया यांच्यातील देवाणघेवाणीच्या करारानुसार लेनिनग्राद येथील स्टेक्लोव्ह गणिती संस्थेत (Steklov Mathematical Institute at Leningrad) जायचे होते. प्राध्यापक आय. एम. मिलिन (I. M. Milin) लेनिनग्रादमध्येच काम करत. त्यांनी १९६४ साली असे एक अनुमान केले होते की जे सिद्ध केले तर बीबरबाखचे अनुमान आपोआप सिद्ध झाले असते. खरे म्हणजे द ब्रान्ज यांनी मिलिन यांचेच अनुमान सिद्ध केले होते. लेनिनग्रादला पोचल्यावर या दोघांची जेव्हा कुणीतरी ओळख करून दिली तेव्हा प्राध्यापक मिलिन यांच्या चेहऱ्यावरील गमतीशीर हावभाव जणू द ब्रान्ज यांच्या सिद्धतेबद्दलची साशंकता दाखवत होते. स्टेक्लोव्ह गणिती संस्थेत भूमितीय फलन सिद्धांत (geometric function theory) यांतील विषयांवर साप्ताहिक चर्चासत्र चालत असे; ते एका वेळी तीन तास चाले. द ब्रान्ज यांनी बोलायला सुरुवात केली तेव्हा त्यांच्या एकाही शब्दावर कोणी विश्वास ठेवायला तयार नव्हते. पण हळूहळू परिस्थिती बदलत गेली. द ब्रान्ज यांच्या दुसऱ्या व्याख्यानानंतर पुढील आठवड्यात त्यांच्या अनुपस्थितीत बाकी सगळे मुद्दाम जमले, आपसात चर्चा करण्यासाठी. तिसऱ्या व्याख्यानाच्या वेळी प्राध्यापक मिलिन यांनी द ब्रान्ज यांच्याबरोबर हस्तांदोलन केले, व डोळ्यांतील चमक जराही कमी न होऊ देता इतकेच म्हणाले, ‘तुमचा युक्तिवाद सुरेख आहे’. द ब्रान्ज यांना पाहिजे होती ती पावती मिळाली होती. प्राध्यापक मिलिन आणि दुसऱ्या एका गणितज्ञाने द ब्रान्ज यांनी दिलेल्या सिद्धतेबाबत लेखी अहवाल सादर केले, काही पर्यायी युक्तिवादही त्यांनी सुचवले. चर्चासत्रात भाग घेणाऱ्या इतरांनी ते अहवाल मान्य केले. द ब्रान्ज यांनी आपल्या सिद्धतेत अतिगुणोत्तरीय फलने (hypergeometric functions) आणि फलनीय विश्लेषण (functional analysis) यांचा वापर केला होता. लेनिनग्रादच्या चर्चासत्रात भाग घेणाऱ्यांनी भूमितीय फलन सिद्धांताच्या पारंपरिक भाषेत, म्हणजे फलनीय विश्लेषण न वापरता, त्या सिद्धतेचे रूपांतरही करून दाखवले. लेनिनग्राद सोडण्यापूर्वी द ब्रान्ज यांनी आणि चर्चासत्राच्या प्रमुखाने कित्येक दिवस खपून, दुपारी दोन ते रात्री दहा असे काम करून, प्रसिद्धिपूर्व लेख (preprints) तयार केले, एक रशियन भाषेत व एक इंग्लिशमध्ये. लेनिनग्रादमधील दहा आठवड्यांच्या वास्तव्यात द ब्रान्ज यांचे वजन दहा किलोंनी कमी झाले होते, पण त्यांची गणिती उंची (mathematical stature) किती तरी वाढली होती.

लुइ द ब्रान्ज
लवकरच जगभरातील गणितज्ञांत ही सनसनाटी बातमी पसरली. बीबरबाखचे अनुमान आता अनुमान राहिले नव्हते, तर ते आता एक प्रमेय झाले होते, व ते द ब्रान्ज यांनी सिद्ध केले होते. निरनिराळ्या कार्यशाळांमध्ये, सेमिनार्समध्ये, परिषदांमध्ये त्याचे सादरीकरण होत गेले. सुरवातीला द ब्रान्ज यांनी आपला शोधनिबंध Matematicheskii Sbornik या रशियन नियतकालिकात प्रसिद्ध करायचे ठरवले होते, पण काही तांत्रिक कारणामुळे ते रद्द करून त्यांनी तो Acta Mathematica या स्विडिश नियतकालिकाकडे १९८४ सालच्या सप्टेंबरमध्ये पाठवला. २७ फेब्रुवारी १९८५ रोजी तो प्रसिद्ध झाला. लेखाच्या शेवटी द ब्रान्ज यांनी बीबरबाखचे अनुमान सिद्ध करण्यात आंतरशाखीय व आंतरराष्ट्रीय सहकार्य (Interdisciplinary and International Cooperation) किती बहुमूल्य ठरले याचा आवर्जून उल्लेख केला आहे. सगळीकडून द ब्रान्ज यांच्यावर स्तुतिसुमनांचा वर्षाव झाला. त्यांना १९८६ साली कॅलिफोर्नियातील बर्कले येथे भरलेल्या गणितज्ञांच्या आंतरराष्ट्रीय महासभेमध्ये (International Congress of Mathematicians) एक प्रमुख वक्ता (plenary speaker) म्हणून आमंत्रण आले.
या कहाणीवरून काही बोध घेता येतील. एक म्हणजे बीबरबाखचे अनुमान गणिताच्या ज्या शाखेचा भाग मानले जाते, त्यापेक्षा वेगळ्या शाखांत द ब्रान्ज काम करत, व कदाचित त्यामुळे त्यांनी मांडलेल्या सिद्धतेची प्रथम कोणी गंभीरपणे दखल घेतली नाही. असे दुर्लक्ष होणे साहजिक असले तरी वाजवी नव्हते. एखादा सक्षम गणितज्ञ, मग तो कुठल्याही शाखेत काम करत का असेना, जर गंभीरपणे प्रस्ताव मांडत असेल, तर त्याच्याकडे दुर्लक्ष करणे योग्य नाही. दुसरे असे की प्राध्यापक गॉस्की यांनी केलेला संगणकाचा वापर निर्णायक ठरला नसला, तरी संगणकाच्या साह्याने गॉस्कींनी n = 30 पर्यंत मारलेली भरारी पाहून द ब्रान्ज यांचा आपल्या सिद्धतेच्या आराखड्यावरील विश्वास दुणावला होता. संगणकाचा मदतनीस म्हणून उपयोग करणे निश्चितच श्रेयस्कर आहे हे पुन्हा एकदा गॉस्कींनी दाखवून दिले. तिसरी गोष्ट अशी की ॲस्की व गॅस्पर यांनी पूर्वी केव्हा तरी काही बहुपदींबाबत करून ठेवलेले काम अचानकपणे द ब्रान्ज यांच्या पथ्यावर पडले होते. गणितातील कुठल्या गोष्टीचा केव्हा उपयोग होईल याचा नेम नसतो. म्हणून गणितातील काहीही काम कालबाह्य वा त्याज्य मानणे योग्य नसते. शेवटची आणि सर्वात महत्त्वाची गोष्ट म्हणजे द ब्रान्ज यांनी आपल्या कामाबद्दल बिलकुल गुप्तता राखली नाही. त्याच्याबद्दल ते अनेकांशी बोलत राहिले. म्हणूनच ते गॉस्कींचा सहयोग मिळवू शकले. योगायोगाने का होइना, पण गॉस्कींनी त्यांच्या मित्राला केलेल्या फोनमुळेच द ब्रान्ज यांना आपल्या सिद्धतेची शेवटची ओळ लिहिता आली. या बौद्धिक देवघेवीवरून उच्च स्तरावर काम करणाऱ्या गणितज्ञांत बाणलेली सचोटी, त्यांचे सौजन्य व प्रामाणिकता हे सगळे स्पष्टपणे प्रकाशात आले. फक्त तार्किकदृष्टया योग्य असलेल्या गणिती सिद्धतेच्या पलिकडे जाणारे हे सद्गुण खरोखर लक्षणीय आहेत.
जगात सगळ्या प्रकारची माणसे असतात. गणितीही त्याला अपवाद नाहीत. बीबरबाखने केलेल्या अनुमानामुळे त्याला प्रसिद्धी मिळाली असली तरी वैयक्तिक पातळीवर तो कुप्रसिद्धच होता. तो कट्टर नाझी होता, त्याने एडमंड लॅन्डाउ (Edmund Landau) व इसाइ शूर (Issai Schur) यांसारख्या थोर ज्यू सहकाऱ्यांना त्यांच्या पदांवरून काढून टाकण्यात हिरिरीने भाग घेतला. इतकेच नव्हे तर ज्युलिअस शौडर (Juliusz Schauder) या महान गणितज्ञाला गेस्टापोच्या स्वाधीन करवले; गेस्टापोने नंतर त्याला ठार मारले.

बीबरबाख, १८८६-१९८२
१९४५ साली दुसरे महायुद्ध संपल्यावर बीबरबाखने केलेल्या कृत्यांमुळे त्याला सर्व विद्याविषयक (academic) पदांवरून काढून टाकण्यात आले. आश्चर्य म्हणजे हे सर्व बाजूला ठेवून १९४९ साली अलेक्झांडर ओस्ट्रॉव्स्की (Alexander Ostrowski) या गणितज्ञाने बीबरबाखला व्याख्यान देण्यासाठी स्वित्झरलंडमधील बाझल विद्यापीठात (University of Basel) बोलावले होते, ओस्ट्रॉव्स्की लॅन्डाउचा विद्यार्थी होता तरीही!
---
बालमोहन लिमये
(balmohan.limaye@gmail.com)

लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण
ललित लेखनाचा प्रकार
हा आणि मागचा, हे दोन्ही लेख
हा आणि मागचा, हे दोन्ही लेख अतिशय ओघवते आणि समजायला सोपे झाले आहेत.
अर्थात माझ्या दृष्टीने समजायला सोपे म्हणजे साधारण एक आठवडा वेळ मिळेल तसं वाचून समजतील असे! :D
हे दोन्ही लेख वाचत असताना असं लक्षात आलं की हे लेखन असंच चालू राहिलं, तर गणिती लेखनासाठी म्हणून वापरता येणारा एक इंग्रजी - मराठी शब्दकोश तयार करता येईल. अर्थात, हे लेखनाच्या ओघात येणारेच शब्द असल्यामुळे तो exhaustive (यासाठी काही केल्या प्रतिशब्द आठवला नाही!) होणार नाही. पण आंतरजालावर मराठीतून गणिताबद्दल लिहू पाहणाऱ्या तरुण लेखक/लेखिकांना नक्कीच उपयोग होईल.
तसा एक शब्दकोश आहे शासनाचा.
इथे पाहा-
https://shabdakosh.marathi.gov.in/ananya-glossary/9
हा प्रतिसाद दुसरीकडेही डकवला होता. ( https://aisiakshare.com/comment/reply/8241/191093 )
गणित तरीही ललित-लेख
प्रा लिमये यांच्या "गणिताच्या निमित्ताने" या लेखमालेच्या कोणत्याही लेखासाठी टिपण्णी म्हणून सदर मजकूर वाचावा.
जरी लेखांचा मध्यवर्ती विषय त्यांच्या तज्ञतेचा म्हणजेच गणित संदर्भात राहिला तरी त्यात नेहमीच गणिती आणि त्याचे माणूसपण किंवा गणिती आणि त्याच्या संपर्कातील माणसांचे संबंध, हा विषय न चुकता लिहिला गेला. ही संरचनाच लेखमाला सर्वं वाचकांसाठी म्हणून सर्वसमावेशक झाली. यातच लेखकाचे "लालित्य" सिद्ध झाले. त्यातही कोणत्याही विषयातील प्रगती माणूसकेंदित असावी आणि तशी असतेही हे कालांतराने का होईना सिद्ध होते; हेच लिखाणाचे केंद्रीभूत सूत्र दिसते. शिवाय, माणसांतील संबंधांना कोणत्याही भिंती नसाव्यात हेही लेखकाने अनुभवल्याचे दिसते. तज्ज्ञ हा फक्त त्याच्या विषयातील ज्ञानामुळे ओळखला जात नाही तर माणूस म्हणूनही त्याची परीक्षा होत असते हेही वाचावयास मिळाले.
भौतिकशास्त्र, रसायनशास्त्र, वैद्यकीयशास्त्र, तंत्रशास्त्र, निरनिराळ्या कला यातील संशोधन आणि इतर प्रगती ही अल्प काळातच लोकांपुढे येते आणि त्याचे लाभही लगेचच घेतले जातात. या अशा प्रगतीसाठी गणितशास्त्र अपवाद ठरते. परंतु, या लेखांतून हे स्पष्ट होते की या विषयातील संशोधनही काही काळानंतर उपयुक्त ठरते येवढेच नव्हे तर माणसांना त्याचे लाभही मिळतात.
गणितात संशोधन कसे असते याची मला अजिबात कल्पना नव्हती, ते समजले. हा झाला माझा वैय्यक्तिक लाभ.
एखाद्या क्षेत्रातील असे लिखाण खूपच दुर्मिळ आहे म्हणून लेखकाला पुन्हापुन्हा धन्यवाद.
सरांची गणित शिकवण्याची हातोटी
सरांची गणित शिकवण्याची हातोटी तर प्रत्यक्ष अनुभवलीच होती पण तेच गणित आपल्या मातृभाषेतून इतक्या सुलभ पद्धतीने उलगडताना बघून फारच भारी वाटलं !! हे लेखन अनेक लोकांना गणितातील अवघड संकल्पना आणि काही मूलभूत प्रश्नांची उकल समजून घ्यायला नक्की उपयोगी पडेल तसेच अनेकांना ह्यातून गणित 'वाचायची' सवय लागेल.
सर, ही लेखमाला वाचताना तुम्ही प्रत्यक्ष बोलत आहात असंच वाटलं !!

वाचतो आहे.
गणिती सूत्र डिजिटल पेजवर लिहिण्यासाठी मागे उल्लेख झाला आहे Latex softwareचा. तर ते वापरूनच लिहिले आहेत का लेख?