पायथागोरसचे प्रमेय - भाग ३
पायथागोरसचे प्रमेय
(मी शाळेत न शिकलेले पण आय. आय. टी.त शिकवलेले)
बालमोहन लिमये
हे लेख नंदा खरे यांच्या स्मृतीला अर्पण, ज्यांनी मला लिहिते केले.
भाग ३
उच्चतर मितींमधील पायथागोरसचे प्रमेय
सरळ रेषा एक मितीची, प्रतल दोन मितींचे आणि जिथे आपला वावर असतो ते अवकाश तीन मितींचे असे आपण मानतो. मग यापेक्षा जास्त म्हणजे चार मितींचे विश्व कसे असू शकेल हा प्रश्न पडणे साहजिक आहे. पुढचा प्रश्न असा की अशा विश्वाचा विचार करण्याचे प्रयोजन काय असू शकते. या प्रश्नांची उत्तरे शोधण्याअगोदर आपण आतापर्यंत अभ्यासलेल्या तीन मितींच्या अवकाशातील बिंदू काय दर्शवू शकतो हे बघू. या बिंदूचा निर्देश आपण A = (a1, a2, a3) असा केला आहे. येथील a1, a2, a3 या संख्यांपैकी a1 ही संख्या A या बिंदूचे O = (0, 0, 0) या आरंभबिंदूपासूनचे पूर्व-पश्चिम अंतर दाखवते, a2 ही संख्या उत्तर-दक्षिण अंतर, तर a3 ही संख्या प्रतलाच्या वर-खाली असणारे अंतर. पण सारासार विचार केला तर कळून येईल की या संख्यांनी अंतरे दाखवली पाहिजेत असे बिलकुल नाही. या तीन संख्या A या बिंदूचे तीन गुणविशेष (attributes) दाखवत आहेत आणि ते गुणविशेष एकमेकांवर अवलंबून नाहीत इतकेच. उदाहरणार्थ, एखाद्या बिंदूचे O या आरंभबिंदूपासूनचे पूर्व-पश्चिम अंतर अमुक असले तरी त्याचे उत्तर-दक्षिण अंतर कितीही असू शकते, म्हणजे या दोन गोष्टी (quantities) एकमेकांपासून स्वतंत्र (independent) किंवा एकमेकांशी लंब (orthogonal) आहेत. आता त्या बिंदूचा आणखी एखादा गुणविशेष आपण नक्कीच विचारात घेऊ शकतो. उदाहरणार्थ, एका सुरुवातीच्या क्षणापासून ती घटना होण्याचा काळ. पृथ्वीची उत्पत्ती सुमारे साडेचार अब्ज वर्षांपूर्वी झाली असली तरी आपण ती 0 (शून्य) या क्षणी झाली असे मानू या. त्या क्षणाच्या आधीही काही ग्रह-तारे निर्माण झाले होते आणि नंतर ही होत आहेत. मग a4 या संख्येने आपण A हा बिंदू पृथ्वी उत्पन्न होण्याच्या आधी किंवा नंतर किती वेळाने निर्माण झाला ते दाखवू या; तो बिंदू आधी निर्माण झाला असेल तर a4 ही संख्या ऋण होईल व तो नंतर निर्माण झाला असेल तर a4 ही संख्या धन होईल. तेव्हा आता आपण A = (a1, a2, a3, a4) अशा चार मितींच्या विश्वातील बिंदूंचा विचार करू शकतो, त्यातले पहिले तीन निर्देशांक स्थानासाठी (space) आणि चौथा कालासाठी (time).
दोन मितींच्या प्रतलावरील बिंदूंमधील आणि तीन मितींच्या अवकाशातील बिंदूंमधील अंतराची आपल्याला भौतिक संकल्पना आहे. तिच्याशी सुसंगत अशा पायथागोरसच्या प्रमेयाचा उपयोग करून आपण दुसऱ्या भागात (दुवा) या अंतराचे सूत्र मिळवले. ते सूत्र बिंदूंच्या निर्देशांकांचा एका ठरावीक पद्धतीने वापर करते. पण आता चार मितींच्या विश्वातील बिंदूंमधील अंतराची कोणतीच भौतिक संकल्पना आपल्याला नाही आणि येथे पायथागोरसचे प्रमेयही उपलब्ध नाही. मात्र येथील बिंदूंचे निर्देशांक आपल्याकडे आहेत. मग आपण उलट्या क्रमाने जाऊ शकतो. बिंदूंच्या प्रत्येकी चार निर्देशांकांचा वापर करून आपण त्यांमधील अंतराची व्याख्या (definition) करायची, अगदी आधीच्या सूत्राला साजेशी, आणि त्यांच्या टिंब गुणाकाराची व्याख्याही करायची, अगदी आधीच्या व्याख्येसारखी. दोन आणि तीन मितींमध्ये आरंभबिंदूपासून दोन बिंदूंपर्यंत जाणाऱ्या रेषांचे एकमेकींशी काटकोन करणे आणि त्या दोन बिंदूंचा टिंब गुणाकार शून्य असणे या गोष्टी एकच असल्याचे आपण पाहिले आहे. आता चार मितींच्या विश्वातील दोन रेषा एकमेकींशी कशा काटकोन करतील याचे चित्र आपण डोळ्यासमोर उभे करू शकत नसलो तरी त्याची व्याख्या तेथील दोन बिंदूंचा टिंब गुणाकार शून्य असणे अशी केली की झाले. प्रश्न एवढाच उरतो की हे सगळे केल्यावर आपल्याला पायथागोरसच्या प्रमेयाला साजेसे प्रमेय मिळते की नाही. विश्वात न्याय (fairness) नावाची काही चीज असेल तर आपल्याला असे प्रमेय जरूर मिळाले पाहिजे!
चार मितींच्या विश्वातला आरंभबिंदू आहे O = (0, 0, 0, 0). तेथपासूनचे A = (a1, a2, a3, a4) या बिंदूपर्यंतचे अंतर
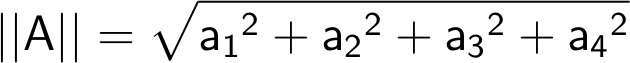
असे निश्चित करू या. आधीप्रमाणेच A = (a1, a2, a3, a4) आणि B = (b1, b2, b3, b4) या चार मितींच्या विश्वातील बिंदूंची बेरीज A + B = (a1 + b1, a2 + b2, a3 + b3, a4 + b4) अशी करायची, आणि A - B = (a1 - b1, a2 - b2, a3 - b3, a4 - b4) अशी वजाबाकीही. मग A आणि B या बिंदूंमधील अंतर होईल

हे अंतर या दोन बिंदूंच्या चारही गुणविशेषांतील फरकांची एका विशिष्ट रीतीने केलेली गोळाबेरीज आहे. बऱ्याच प्रसंगी दोन बिंदूंतील सर्वसाधारण समानता किंवा असमानता जाणण्यासाठी ही गोळाबेरीज उपयोगी पडते. या दोन बिंदूंचा टिंब गुणाकार A·B = a1 b1 + a2b2 + a3 b3 + a4 b4 असा करायचा, आणि OA आणि OB काटकोनात असणे याची व्याख्या A आणि B या बिंदूंचा टिंब गुणाकार शून्य असणे अशी करायची. आधीप्रमाणेच A·A = ||A ||2 ही समानता स्पष्ट आहे.
उदाहरणार्थ, A = (3, 4, 1, 2) आणि B = (1, 2, 1, -1) हे चार मितींच्या विश्वातले बिंदू विचारात घेऊ या. मग ||A||2 = 9 + 16 + 1 + 4 = 30, व म्हणून A या बिंदूचे आरंभबिंदूपासूनचे अंतर √30. तसेच या दोन बिंदूंची बेरीज आहे A + B = (3+1, 4+2, 1+1, 2 -1) = (4, 6, 2, 1), व त्यांचा टिंब गुणाकार आहे A·B = 3 + 8 + 1 – 2 = 10. त्याचप्रमाणे A – B = (3-1, 4-2, 1-1, 2 +1) = (2, 2, 0, 3) आणि ||A - B||2 = 4 + 2 + 0 + 9 = 15, व म्हणून या दोन बिंदूंमधील अंतर आहे √15. सांगायचा मुद्दा असा की या सर्व गोष्टी दोन मितींच्या प्रतलावरील बिंदूंच्या व तीन मितींच्या अवकाशातील बिंदूंच्या अगदी हुबेहूब आहेत.
असे म्हणतात की सुयोग्य व्याख्या केल्या की अपेक्षित उत्तरे सहज मिळून जातात. पायथागोरसच्या प्रमेयाचे तसेच आहे: चार मितींच्या विश्वातील A, B, C, D या बिंदूंपैकी प्रत्येकी दोन बिंदूंचा (pairwise) टिंब गुणाकार जर शून्य असेल, म्हणजेच OA, OB, OC, OD युग्मतः (pairwise) काटकोनात असतील, तर

हे विधान सिद्ध करण्यासाठी फक्त वरील समीकरणाच्या डाव्या आणि उजव्या बाजूंची उकल केली की झाले. या प्रमेयाचे सर्वांत सोपे उदाहरण देण्यासाठी a, b, c, d या चार संख्या घेऊ या. मग A = (a, 0, 0, 0), B = (0, b, 0, 0), C = (0, 0, c, 0), D = (0, 0, 0, d) या बिंदूंपैकी प्रत्येकी दोन बिंदूंचा टिंब गुणाकार शून्य आहे. शिवाय ||A||2 = a2, ||B||2 = b2 , ||C||2 = c2, ||D||2 = d2, व म्हणून पायथागोरसच्या प्रमेयानुसार ||A + B + C + D||2 = a2 + b2 + c2 + d2, आणि ते बरोबरच आहे कारण A + B + C + D = (a, b, c, d).
चार मितींतील बिंदूंचे कल्पनाचित्र मनात आणणे (visualization) आपल्याला अशक्य कोटीतील वाटणारच. असे चित्र स्पष्टपणे मनःचक्षूंपुढे आणू शकणारा विल्यम थर्स्टन (William Thurston) सारखा गणितज्ञ विरळाच. काही वेळा चार मितींच्या वस्तूचा एखादा त्रिमितीय तुकडा (three dimensional slice) आपण प्रयत्नपूर्वक बघू शकतो. मात्र असे तुकडे एकमेकांबरोबर कसे रचले असले पाहिजेत हे सांगणे कठीणच. पण अशा कल्पनाचित्रामुळे हातातील विषयाचे काही प्रमाणात आकलन होऊन नवनवीन दुवे शोधून काढायला मदत निश्चित होते. बऱ्याच प्रसंगी डोळ्यापुढे काही रेखाटन नसतानाही तीन मितींत उपलब्ध असलेल्या निष्पत्तींवरून साधर्म्याचा (analogy) उपयोग करून उच्चतर (तीनपेक्षा अधिक) मितींमधील विधाने गणितज्ञ मांडू शकतात व त्यांच्या सिद्धता देऊ शकतात. आताचेच पाहा ना, चार मितींतील रेषा कशा दिसतात आणि दोन रेषा काटकोनात कशा छेदतात याची कल्पनाही नसताना आपण चार मितींमधील पायथागोरसचे प्रमेय मिळवले आहे. त्यासाठी चौथ्या मितीचे भौतिक किंवा आधिभौतिक (physical or metaphysical) अस्तित्व मानण्याची काहीच गरज नाही.
येथे एक सावधानतेची सूचना देणे जरूर आहे. भौतिकी (physics) या विषयातील सापेक्षता सिद्धांत (relativity theory) शिकताना बऱ्याच जणांनी मिन्कावस्कीचे अवकाशकाल (Minkowski spacetime) अभ्यासले असेल. हे अवकाशकालही चार मितींचे असते आणि त्यातील बिंदूंचा निर्देशही A = (a1, a2, a3, a4), B = (b1, b2, b3, b4) असाच करता येतो, मात्र A·B = a1 b1 + a2b2 + a3 b3 + a4 b4 या आपल्या टिंब गुणाकाराऐवजी A*B = a1 b1 + a2b2 + a3 b3 - a4 b4 हा सापेक्षीय टिंब गुणाकार (relativistic dot product) वापरला जातो. त्यामुळे सगळे वळणच बदलून जाते, कारण A = (a1, a2, a3, a4) या बिंदूच्या आरंभबिंदूपासूनच्या 'अंतरा'चा वर्ग A*A = a12 + a22 + a32 - a42 हा धन, ऋण किंवा शून्य असू शकतो. सापेक्षतावादात A*A जर धन असेल म्हणजे a12 + a22 + a32 > a42, तर A या बिंदूला अवकाशसदृश (spacelike) म्हणतात, जर A*A ऋण असेल म्हणजे a12 + a22 + a32 < a42, तर A या बिंदूला कालसदृश (timelike) म्हणतात व जर A*A शून्य असेल म्हणजे a12 + a22 + a32 = a42, तर A या बिंदूला प्रकाशसदृश (lightlike) म्हणतात. ही कथा इथेच थांबवू या, एवढेच सांगून की आपण विचारात घेतलेले, चार मितींचे विश्व साधे सोपे आहे, तीन मितींच्या अवकाशातील युक्लिडीय संकल्पनांचे स्वाभाविक वर्धन (natural extension) करून, पुढे वाढवून मिळवलेले; त्याला कधी कधी सपाट अवकाशकाल (flat spacetime) असेही म्हणतात, कारण मिन्कावस्कीचे अवकाशकाल वक्र (curved) असते ना!
खरे म्हणजे चौथी मिती काल दर्शवते असे आपण फक्त उदाहरणादाखल समजले आहे, ती बिंदूंचा अन्य गुणविशेषही दर्शवू शकते. चार मितींच्याही पुढे जायचे असेल तर आणखी एका गुणविशेषाचा विचार करता येईल. उदाहरणार्थ, आवाजाची वारंवारता (frequency). एका विशिष्ट आवाजाच्या मध्य सप्तकातील 'सा' हा सूर आपण या गुणविशेषाचा आरंभबिंदू म्हणजे 0 (शून्य) मानू या, जसे काळी चार (G Sharp) या हार्मोनियमवरील पट्टीचा सूर. मग मध्य सप्तकातील रे, ग, म, प, ध, नि या सुरांचा आणि पुढे जाऊन तार, अतितार इत्यादी सप्तकांतील सुरांचा धन संख्यांनी निर्देश करता येईल, तर मंद्र, अतिमंद्र इत्यादी सप्तकांतील सुरांचा निर्देश ऋण संख्यांनी. एखादी व्यक्ती गात असताना तिच्या आवाजाचा याप्रकारे निर्देश करणाऱ्या संख्येला आपण a5 असे म्हटले तर A = (a1, a2, a3, a4, a5) हा पाच मितींच्या विश्वातील बिंदू होईल, व अशा A, B, C , D, E या पाच बिंदूंसाठी पायथागोरसचे प्रमेय मांडता येईल. (या पाच मिती म्हणजे, पहिल्या तीन स्थानदर्शक, चौथी कालदर्शक आणि पाचवी सुरांची पट्टी किंवा आवाजाची वारंवारता.)
आता पाच काय, पाचशे काय, कितीही मितींच्या विश्वातील बिंदूंसाठी पायथागोरसचे प्रमेय सहज मिळू शकते. समजा n हा एक धन पूर्णांक आहे, आणि आपल्याला n मितींतील पायथागोरसचे प्रमेय हवे आहे. जर n हा पूर्णांक 26 पेक्षा मोठा असेल, तर इंग्लिश वर्णमालेतील (alphabet) A, B, . . ., Y, Z ही अक्षरे n बिंदू दाखवण्यासाठी पुरणार नाहीत. म्हणून त्यांऐवजी A1, A2, . . ., An ही A या एकाच अक्षराला 1, 2, . . ., n असे पादांक (subscript) दिलेली चिन्हे वापरू या. आता आपला आरंभबिंदू O = (0, 0, . . ., 0) याचे सर्व n निर्देशांक 0 (शून्य) आहेत, आणि A = (a1, a2, . . ., an) या n मितींच्या विश्वातील बिंदूचे आरंभबिंदूपासूनचे अंतर आहे

तसेच A = (a1, a2, . . ., an) आणि B = (b1, b2, . . ., bn) या n मितींच्या विश्वातील बिंदूंची बेरीज A + B = (a1 + b1, a2 + b2, ..., an + bn) अशी करायची, आणि त्यांचा टिंब गुणाकार A·B = a1 b1 + a2 b2 + … + an bn असा करायचा.
n मितींच्या विश्वातील A1, A2, . . ., An या बिंदूंपैकी प्रत्येकी दोन (pairwise) बिंदूंचा टिंब गुणाकार जर 0 (शून्य) असेल, म्हणजेच OA1, OA2, . . ., OAn युग्मतः (pairwise) काटकोनात असतील, तर पायथागोरसचे प्रमेय सांगते की
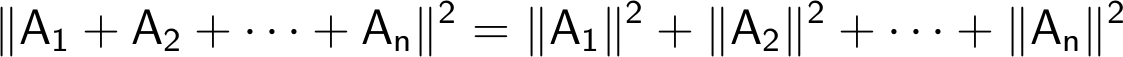
या विधानाची नव्याने सिद्धता देण्याची गरज नाही. पण प्रश्न असा उरतो की असा मोठमोठ्या मितींच्या विश्वाचा हव्यास कशाला धरायचा. आपण पाहिले आहे की प्रत्येक मिती बिंदूंचा एक गुणविशेष दर्शवण्यासाठी वापरता येते. सध्याच्या संगणक युगात प्रत्येक गोष्टीची आधारसामग्री (data) इतकी अतोनात वाढली आहे की एकमेकांचा संबंध नसलेल्या कोट्यवधी गुणविशेषांची माहिती जमा करून ठेवली जात आहे. त्यामुळे मितींची भयंकर वाढ करणे जरूर होत आहे. आपण आतापर्यंत उभारलेली गणिती चौकट (framework) मात्र अशी कितीही वाढ खपवून घेईल. हेच तर गणिताचे वैशिष्ट्य आहे.
अनंत मितींचे विश्व
मोठमोठ्या मितींचा विचार करूनही गणितज्ञ थांबत नाहीत. त्यांना अनंत मितींच्या विश्वाला गवसणी घालायची असते. अशा विश्वातील प्रत्येक बिंदूचे अनंत निर्देशांक असतात. ते सगळे लिहून दाखवायला लागले तर कधीच संपणार नाहीत, म्हणून त्यांपैकी पहिले दोनच निर्देशांक लिहून त्यानंतर . . . अशी तीन टिंबे काढून 'हे संपत नाहीत' असे सुचवले जाते. थोडक्यात, अनंत मितींच्या विश्वातील बिंदू आपण A = (a1, a2, . . .) असा लिहू, आणि आरंभबिंदू O = (0, 0, . . .) असा लिहू. जर B = (b1, b2, . . .) हा देखील तिथला बिंदू असेल, तर A + B = (a1 + b1, a2 + b2, . . .) अशी बेरीज करायला काहीच अडचण नाही. आता A या बिंदूचे आरंभबिंदूपासूनचे अंतर
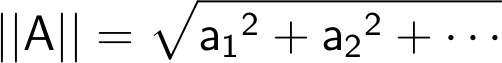
असे लिहिणे क्रमप्राप्त ठरते, पण इथे एक मोठा प्रश्न निर्माण होतो. तो असा की a12, a22, . . . या अनंत संख्यांची बेरीज करत राहायची म्हणजे नेमके काय करायचे? एक गोष्ट लक्षात ठेवू या की a12, a22, . . . यापैकी प्रत्येक संख्या कुठल्यातरी संख्येचा वर्ग असल्याने ती कधीच ऋण नसते. पण आपण जसजशी जास्त संख्याची बेरीज करत जाऊ, तसतशी ती अवाढव्य बनत गेली तर आपण कुठल्याच ठरावीक संख्येपर्यंत पोचणार नाही. उदाहरणार्थ, प्रत्येक nसाठी an2 + 12 + · · · + 12 = n ही मोठमोठी होत जाणारी संख्या मिळते. त्यामुळे a12 + a22 + · · · अशी या अनंत संख्यांची बेरीज करताच येणार नाही. मग असे मनात येईल की प्रत्येक nबरोबर लहान होत जाणारी an अशी संख्या घेतली तर त्या अनंत संख्यांची बेरीज करता यावी. पण तसेही नाही. उदाहरणार्थ, प्रत्येक nसाठी an = 1/√ n अशी लहान होत जाणारी संख्या घेऊ या. मग गणिती विगमन पद्धतीने (Method of Mathematical Induction)

असे दाखवता येते. त्यामुळे पहिल्या 2n टप्प्यांनंतर मिळणारी बेरीज निदान 1 + n/2, व म्हणून अमर्यादच होत जाते, व म्हणून a12 + a22 + · · · अशी या लहान होत जाणाऱ्या अनंत संख्यांचीदेखील बेरीज करता येत नाही.
गणितज्ञ अशा बिकट परिस्थितीतूनही मार्ग काढायचा प्रयत्न करतात. मनमानी निर्देशांक असलेला बिंदू विचारात घेणे परवडत नसेल, तर बिंदूच्या निर्देशांकांवर काही बंधने पत्करावी लागतात. आपण असे ठरवू या की कितीही टप्प्यांनंतर केलेली a12 + a22 +· · · + an2 ही बेरीज जर एका मर्यादेच्या बाहेर जात नसेल, तरच A = (a1, a2, . . .) या बिंदूचा स्वीकार करायचा. उदाहरणार्थ, प्रत्येक n साठी an = 1/n अशी संख्या घेतली, तर गणिती विगमन पद्धतीने

असे दाखवता येते, व म्हणून आपण कितीही टप्प्यांनंतर केलेल्या बेरजेवरील 2 ही मर्यादा स्पष्ट होते. त्यामुळे (1, ½, ⅓, ¼ …) या बिंदूचा आपण स्वीकार करायचा. उपर्युक्त बंधन पाळणाऱ्या बिंदूंच्या विश्वाला ℓ2 असे नाव आहे (उच्चार: लिटल एल्टू). उदाहरणार्थ, (1, 1, …) हा बिंदू या विश्वात नाही, पण (1, ½, ⅓, ¼ …) हा बिंदू या विश्वात आहे. जर A = (a1, a2, . . .) हा बिंदू ℓ2 विश्वात असेल, तर वाढत्या nबरोबर a12 + a22 +· · · + an2 ही n पदांची बेरीज एका सुनिश्चित संख्येच्या जवळ जाते. ती संख्याच या अनंत पदांची बेरीज असे मानायचे. गणिती विश्लेषण (Mathematical Analysis) या विषयाच्या सुरुवातीलाच हे सारे शिकवतात. या ℓ2 विश्वातील A = (a1, a2, . . .) बिंदूचे आरंभबिंदूपासूनचे अंतर
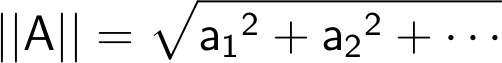
असे लिहिणे आता समर्थनीय ठरते. उदाहरणार्थ, A = (1, ½, ⅓, ¼ …) या ℓ2 विश्वातील बिंदूसाठी ||A||2 म्हणजे
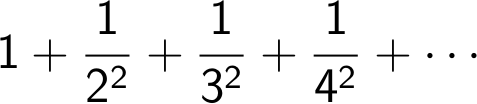
ही अनंत संख्यांची बेरीज किती असावी हा प्रश्न पडणे साहजिक आहे. तो प्रश्न प्रथम लिओनार्ड ऑयलर (Leonhard Euler) या स्विस गणितज्ञाने 1785 साली सोडवला; त्याचे उत्तर आहे π2/6.
जर A = (a1, a2, . . .) आणि B = (b1, b2, . . .) हे बिंदू ℓ2 विश्वात असले तर A + B हा बिंदूही ℓ2 विश्वात असतो; शिवाय त्यांचा टिंब गुणाकार A·B = a1 b1 + a2 b2 + · · · सुद्धा करता येतो. हा टिंब गुणाकार शून्य असणे याचा अर्थ OA आणि OB काटकोनात आहेत असा समजायचा. उदाहरणार्थ, A = (1, 0, ½, 0, ⅓, 0, . . .) आणि B = (0, 1, 0, ½, 0, ⅓, 0, . . .) हे बिंदू ℓ2 विश्वात आहेत आणि त्यांचा टिंब गुणाकार शून्य आहे हे उघड आहे, व म्हणून OA आणि OB काटकोनात आहेत. तसेच फक्त एकच निर्देशांक 1 आणि बाकी सगळे निर्देशांक 0 (शून्य) असणाऱ्या E1 = (1, 0, 0, . . .), E2 = (0, 1, 0, 0, . . .), . . ., En = (0, . . . ,1, 0, 0, . . .), . . . ह्या अनंत बिंदूंचा ℓ2 विश्वात समावेश होतो, व त्यांपैकी प्रत्येक बिंदूचा उरलेल्या सर्व बिंदूंबरोबर केलेला टिंब गुणाकार शून्य आहे. यांतील प्रत्येक बिंदू एक वेगळी मिती दर्शवत असल्याने ℓ2 हे विश्व अनंत मितींचे आहे.
आता ℓ2 या अनंत मितींच्या विश्वातील पायथागोरसचे प्रमेय मांडू या. समजा A1 , A2 . . . हे ℓ2 विश्वातील अनंत बिंदू आहेत आणि त्यांपैकी प्रत्येकी दोन बिंदूंचा टिंब गुणाकार शून्य आहे, म्हणजेच OA1, OA2, . . . युग्मतः (pairwise) काटकोनात आहेत. जर (||A1||, ||A2||, . . .) हा बिंदूही ℓ2 मध्ये असेल, तर A1 + A2 + · · · ही ℓ2 विश्वातील अनंत पदांची बेरीज ℓ2 मध्येच असते, व
|| A1 + A2 + · · ·||2 = ||A1 ||2 + || A2 ||2 + · · ·.
या विधानाची सिद्धता मात्र आधीसारखी सोपी नाही; ती ℓ2 या अनंत मितींच्या विश्वाच्या काही खास गुणधर्मांवर अवलंबून आहे; ते गुणधर्म इथे सांगणे अप्रस्तुत होईल. याप्रकारचे अनंत मितींच्या विश्वातील विधान केवळ गणिती उत्सुकता शमवत नाही, तर विदाविज्ञानासाठी (data science) लागणाऱ्या अवाढव्य मितींच्या विश्वांतील विधानांचे ते एक आदर्शीकृत प्रतिमान (idealized model) बनून राहते.
ℓ2 या विविक्त (discrete) स्वरूपाच्या विश्वाचे एक संतत प्रतिरूप (continuous analogue) विचारात घेता येते. हे प्रतिरूपी विश्व ℒ2 या नावाने ओळखले जाते (उच्चार: कॅपिटल एल्टू). त्यातील बिंदू a1, a2, . . . अशा अनंत निर्देशांकांनी ठरत नाही, तर तो एका रेषाखंडावर सुनिश्चित केलेल्या (defined) विशिष्ट प्रकारच्या फलनाने (function) ठरतो. ℒ2 विश्वातील अशा दोन बिंदूंचा टिंब गुणाकार म्हणजे त्या दोन फलनांच्या गुणाकाराचा संकलक (integral). या गुणाकाराला आंतर गुणाकार (inner product) असेही नाव आहे. गणिताच्या अनेक शाखांत वापरल्या जाणाऱ्या व निरनिराळ्या शास्त्रांमध्ये उपयोगी ठरलेल्या फूरिए श्रेणीची (Fourier series) परिपूर्ण कथा याच ℒ2 विश्वात सांगता येते. त्याच्याही पलिकडे जाऊन एका अमूर्त (abstract) स्वरूपाच्या विश्वात पायथागोरसचे प्रमेय मांडता येते. डेव्हिड हिलबर्ट (David Hilbert) या जर्मन गणितज्ञाने विसाव्या शतकाच्या पहिल्या दशकात हे विश्व प्रस्तुत केले; त्याला हिलबर्टचे अवकाश (Hilbert space) असेच म्हणतात.

डेव्हिड हिलबर्ट 1912मध्ये
या भव्य व्यापकीकरणाचा (grand generalization) वापर पुंजयामिकीसारख्या (Quantum Mechanics) क्षेत्रांमध्ये सर्रास होत असतो. गणिताच्या फलनीय विश्लेषण (Functional Analysis) या विषयावरील पाठ्यपुस्तकांत ही चर्चा उपलब्ध होऊ शकते. मुंबई येथील आय. आय. टी.मध्ये एम. एस्सी.च्या दुसऱ्या वर्षातील मुलांना हा विषय मी शिकवत असे. तेव्हा एक स्वाध्याय (exercise) म्हणून हिलबर्टच्या अवकाशातील पायथागोरसचे प्रमेय शिकवण्याचा योग आला, मीच लिहिलेल्या पुस्तकातून. त्यावेळी पुण्याला शाळेत शिकत असताना भूमितीमधील पायथागोरसच्या प्रमेयाकडे मी का दुर्लक्ष केले असे राहून राहून वाटत होते.
(समाप्त)
---
बालमोहन लिमये
(balmohan.limaye@gmail.com)

लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण
माहितीमधल्या टर्म्स
Infinite Addition
It depends on how you add all positive integers with all negative integers. If you write a_n = n + (-n), then each a_n is zero and the sum of all the a_n's is zero. If you write b_n = n + [-(n-1)], then each b_n is 1 and the sum of all the b_n's is infinity, while if you write c_n = n + [-(n+1)], then each c_n is -1 and the sum of all the c_n's is minus infinity. You can group the positive and negative integers differently to get different answers!
रोचक!
सर्व सम पूर्णांकाची “संख्या” ही सर्व पूर्णांकांच्या “संख्ये”इतकीच आहे, या कल्पनेने भंजाळायला होते, तसेच आहे हे!
(अवांतर: अनंत संख्यांची “बेरीज” या संकल्पनेस काही अर्थ आहे काय? की हा इन्फिनिट सीरीज़ - लिमिट (अॅज़ एन टेंड्ज़ टू इन्फिनिटी)मधला प्रकार धरायचा?)
(तरीसुद्धा, एकाच सीरीज़ची एकाहून अधिक लिमिटे, हे पचत नाही.)
मोघम/जुजबी
मी फक्त मोघम किंवा जुजबी प्रतिक्रिया दिली होती. उत्सुकता पूर्ण मिटवायची असेल तर अनंत क्रमिका (infinite sequence) व अनंत श्रेणी (infinite series) यांचे अभिसरण (convergence) व केवल अभिसरण (absolute convergence) या सगळ्याचा मुळातून अभ्यास करावा लागेल. अशी शिकवणी इथे देणे योग्य होणार नाही.

The series
It is amazing how Prof. Limaye can lead the reader from very simple, familiar math to fairly complicated concepts without boring. A somewhat irrelevant factoid: In University of Goettingen, there is a room called Hilbertsraum (Hilbert's room, but also Hilbert space)! Apparently, Banach space is too abstract for such a visible realization:-)