गणिताच्या निमित्ताने – भाग १० [फर्माचे विधान]

बालमोहन लिमये

(फर्माचे विधान सिद्ध करण्यासाठी जगभरातले गणितज्ञ तीनशेहून अधिक वर्षे झगडत होते. त्यामागचा चित्तथरारक घटनाक्रम – प्राध्यापक बालमोहन लिमये यांच्या साप्ताहिक लेखमालेतील पुढील भाग. मागील भाग इथे.)

फर्माचे विधान

१९९५ सालाच्या मध्याला मला माझा मित्र तरलोक शोरी याची एक इमेल आली, फक्त एका वाक्याची, ‘फर्माचे विधान खरे ठरले’ असे सांगणारी. फर्माचे विधान काय होते ते मला माहीत होते आणि ते सिद्ध करण्यासाठी जगभरातले गणितज्ञ तीनशेहून अधिक वर्षे झगडत होते हेही मी जाणून होतो. आता ते कुणी व कसे सिद्ध केले याबद्दल उत्सुकता वाटणे साहजिक होते.

पण त्याआधी जे नाट्यमय प्रसंग घडले होते ते तरलोकला तेव्हा माहीत होते की नाही याची मला कल्पना नाही; मला तरी त्यांची मुळीच कल्पना नव्हती. अंकशास्त्रात संशोधन करणाऱ्या हाताच्या बोटांवर मोजता येतील इतक्या गणितज्ञांखेरीज इतरांसाठी हे बराच काळ गौडबंगालच होते. फर्माच्या विधानाची सिद्धता काही रोखठोकपणे थेट मिळाली नव्हती. बऱ्याच गोष्टींचा परिपाक म्हणून ती मिळत होती, अगदी हातातून निसटता निसटता पकडून ठेवावी अशी.

फर्माचे विधान एक प्रकारच्या समीकरणांच्या उत्तरांबाबत आहे. 1, 2, 3, . . . या आकड्यांना आपण नैसर्गिक संख्या असे म्हणतो, आपल्याला उत्तरे या संख्यांतच शोधायची आहेत. कॅटलानच्या x^m – yⁿ = 1 या समीकरणाचे एकच उत्तर असते, व ते x = 3, y = 2, m = 2 आणि n = 3 घेऊन मिळते (कारण 3² - 2³ = 9 – 8 = 1) हे आपण आधीच्या एका लेखात पाहिले आहे. अशाच आणखी एका समीकरणाच्या उत्तरांबद्दल फर्माने एक विधान केले होते. समजा n ही नैसर्गिक संख्या आपल्याला दिलेली आहे, आणि x, y, z अशा नैसर्गिक संख्या शोधून काढायच्या आहेत की जेणेकरून xⁿ + yⁿ = zⁿ हे समीकरण साध्य होईल.

प्रथम समजू या n = 1. मग आपले समीकरण होते x + y = z. या समीकरणाची सगळी उत्तरे मिळवणे अगदी सोपे आहे. x आणि y या कुठल्याही नैसर्गिक संख्या घेतल्या आणि z ही त्यांची बेरीज करून मिळणारी नैसर्गिक संख्या घेतली, तर x + y = z हे समीकरण आपोआप साध्य होते. उदाहरणार्थ, x = 3 आणि y = 4 घेतले, तर आपण z = 7 घ्यायचे.

आता समजू या n = 2. मग आपले समीकरण होते x² + y² = z². शाळेत भूमिती शिकताना हे समीकरण आपल्याला भेटले होते. काटकोन त्रिकोणातील काटकोनालगतच्या बाजू जर x आणि y लांबीच्या असल्या आणि कर्णाची लांबी z असेल, तर पायथॅगोरस (Pythagoras) ह्या ग्रीक गणितज्ञाच्या नावाने प्रसिद्ध असलेल्या सिद्धांतानुसार हे समीकरण साध्य होते. फक्त आपल्याला x, y आणि z या तिन्ही नैसर्गिक संख्या आहेत याची खातरजमा केली पाहिजे इतकेच. अशा (x, y, z) त्रिकूटाला पायथॅगोरसचे त्रिकूट (Pythagorean triple) असे म्हणतात. उदाहरणार्थ, (3, 4, 5) आणि (5, 12, 13) ही पायथॅगोरसची त्रिकूटे आहेत, कारण 3² + 4² = 5² आणि 5² + 12² = 13². अशी त्रिकूटे मिळवण्यासाठी युक्लिडचे सूत्र (Euclid’s formula) वापरता येते. ते असे आहे. m आणि n अशा नैसर्गिक संख्या घ्यायच्या की m ही nपेक्षा मोठी आहे. आता x, y आणि z या नैसर्गिक संख्यांची व्याख्या पुढीलप्रमाणे करायची :

याप्रमाणे (x, y, z) हे पायथॅगोरसचे त्रिकूट बनते. उदाहरणार्थ, m = 4 आणि n = 1 घेतल्यास, x = 15, y = 8, आणि z = 17, व (15, 8, 17) हे पायथॅगोरसचे त्रिकूट आपल्याला मिळते. शिवाय (x, y, z) हे जर पायथॅगोरसचे त्रिकूट असले, तर (y, x, z) हे पायथॅगोरसचे त्रिकूट असतेच, आणि k ही कोणतीही नैसर्गिक संख्या असेल तर (kx, ky, kz) हे देखील पायथॅगोरसचे त्रिकूट असते. या प्रकारे पायथॅगोरसची सर्व त्रिकूटे मिळतात, आणि x² + y² = z² या समीकरणाची सगळी उत्तरे आपण मिळवू शकतो. अर्थातच ही उत्तरे अनंत आहेत.

आता समजू या n = 3. मग आपले समीकरण होते x³ + y³ = z³. या समीकरणाचे उत्तर शोधणे नुसते कठीण नाही, तर ते अशक्यप्राय होऊन बसते. पिएर द फर्मा (Pierre de Fermat, १६०७ - १६६५) या फ्रेंच गणितज्ञाने या समीकरणाची, आणि n ही नैसर्गिक संख्या 3 पेक्षा मोठी असेल तर xⁿ + yⁿ = zⁿ या समीकरणाचीही उत्तरे शोधण्याचा आटोकाट प्रयत्न केला. पण त्याला एकही उत्तर मिळाले नाही. डायोफँटस् (Diophantus) या ग्रीक लेखकाने लिहिलेल्या अरिथमॅटिका (Arithmetica) नावाच्या पुस्तकाची एक प्रत फर्माकडे होती. आपल्या प्रतीवर फर्माने लिहून ठेवले होते की वरील समीकरणांना एकही उत्तर नसते, व याची एक खरोखर आश्चर्यकारक सिद्धता त्याच्या डोक्यात आहे, पण त्या पुस्तकाचा समास ती लिहून काढायला पुरेसा नाही. ही गोष्ट आहे १६३७ सालाच्या सुमाराची. तेव्हापासून ‘जर n ही नैसर्गिक संख्या दोनपेक्षा मोठी असेल, तर xⁿ + yⁿ = zⁿ हे समीकरण साध्य करणाऱ्या x, y, z अशा नैसर्गिक संख्या नसतात’ या विधानाला फर्माचा शेवटचा सिद्धांत (Fermat’s Last Theorem) असे नाव मिळाले, कुणालाही त्याची सिद्धता माहीत नसताना. खरे म्हणजे त्याला फर्माचे शेवटचे अनुमान (Fermat’s Last Conjecture) असे संबोधणे उचित होते. आपण त्याला फर्माचे विधान असे संबोधूया.

फर्माच्या इतर लिखाणावरून समजून येते की त्याने फक्त n = 4 या संख्येसाठीच हे विधान सिद्ध केले होते. जर हे विधान n या नैसर्गिक संख्येसाठी सिद्ध करता आले, आणि m ही कुठलीही नैसर्गिक संख्या असेल तर ते विधान k = nm या संख्येसाठी आपोआप सिद्ध होते, कारण x^k + y^k = z^k हे समीकरण आपण (x^m)ⁿ + (y^m)ⁿ = (z^m)ⁿ असेही लिहू शकतो, व जर (x, y, z) या त्रिकूटाने x^k + y^k = z^k हे समीकरण साध्य होत असेल तर (x^m, y^m, z^m) या त्रिकूटाने xⁿ + yⁿ = zⁿ हे समीकरणही साध्य झाले असते.

1 पेक्षा मोठ्या प्रत्येक नैसर्गिक संख्येला मूळ अवयव (prime factors) असतात. एखादी नैसर्गिक संख्या 1 पेक्षा मोठी असेल, व तिला (1 सोडून) दुसऱ्या कोणत्याही नैसर्गिक संख्येने भाग जात नसेल, तर तिला मूळ संख्या (prime number) असे नाव आहे. उदाहरणार्थ, 2, 3, 5, 7, 11 इत्यादी. यांपैकी 2 ही एकच मूळ संख्या सम आहे, व बाकीच्या सगळ्या मूळ संख्या विषम आहेत. आता कुठल्याही दोनपेक्षा मोठ्या नैसर्गिक संख्येला चारने तरी भाग जातो किंवा एका तरी विषम मूळ संख्येने तरी भाग जातो. फर्माने त्याचे विधान चार या संख्येसाठी सिद्ध केले होतेच; आता त्या विधानाची सत्यता 3, 5, 7, ... अशा प्रत्येक विषम मूळ संख्येसाठी सिद्ध केली तर ती सर्व दोनपेक्षा मोठ्या नैसर्गिक संख्यांसाठी सिद्ध झाली असती, म्हणजे फर्माचे विधान पूर्णतः खरे ठरले असते. शंभरपेक्षा जास्त वर्षांनी १७७० साली ऑयलर (Euler) या शास्त्रज्ञाने ते विधान n = 3 साठी सिद्ध केले, १८२५ साली लजान्द्र (Legendre) व डिरिक्ले (Dirichlet) या शास्त्रज्ञांनी ते n = 5 साठी सिद्ध केले, आणि १८३९ साली लामे (Lamé) या गणितज्ञाने ते n = 7 साठी सिद्ध केले. पुढे १८५० साली कुमर (Kummer) या गणितज्ञाने एखादी मूळ संख्या ‘नियमित’ (regular) असते म्हणजे काय याची व्याख्या दिली, आणि अशा सर्व मूळ संख्यांसाठी फर्माचे विधान सिद्ध केले. 31 पर्यंतच्या सगळ्या विषम मूळ संख्या नियमित आहेत. शिवाय 41, 43, 47, 53, 61, 71, 73 अशा कितीतरी मूळसंख्या नियमित आहेत. त्या सगळ्यांसाठी आता फर्माचे विधान खरे ठरले होते. तरीही 37, 59, 67 अशा नियमित नसणाऱ्या ज्या अनंत मूळ संख्या आहेत, त्यांच्यासाठी फर्माच्या विधानाची सत्यता जगातील सर्व गणितज्ञांना हुलकावणी देत राहिली, १९९४ पर्यंत.

फर्माचे विधान सिद्ध करण्याच्या प्रयत्नांतून बऱ्याच नवनवीन संकल्पना पुढे आल्या होत्या. त्यांचा फर्माचे विधान अंशतः सिद्ध करायला उपयोगही झाला. उदाहरणार्थ, ‘n ही कुठलीही विषम मूळ संख्या असेल तर xⁿ + yⁿ = zⁿ या फर्माच्या समीकरणाची उत्तरे अनंत असू शकत नाहीत’ असे सिद्ध करता आले. (येथे जर (x, y, z) हे एक उत्तर असेल, आणि k ही कोणतीही नैसर्गिक संख्या असेल तर (kx, ky, kz) हे उत्तर वेगळे मानायचे नाही.) उलटपक्षी, अशी काही जास्त व्यापक विधाने मांडण्यात आली की ज्यांची सत्यता सिद्ध केल्यास फर्माचे विधान आपोआप सिद्ध व्हावे. जास्त व्यापक विधान सिद्ध करणे जास्त अवघड असणार हे जरी सामान्यतः खरे असले, तरी काही वेळा ते आधीच्या विधानाकडे बघायची एक वेगळी दृष्टी देऊन जाते. असेच काहीसे फर्माच्या विधानाबद्दल झाले. १९५४ साली तानियामा (Taniyama) व शिमुरा (Shimura) या दोन जपानी गणितज्ञांनी एक महत्त्वाचे अनुमान प्रस्तुत केले. गणितातील दोन अगदी वेगळ्या शाखांतील प्रश्नांचा जवळचा नातेसंबंध असल्याचा त्यांचा प्रस्ताव होता. a, b आणि c या परिमेय (rational) संख्या असतील, म्हणजे त्या दोन नैसर्गिक संख्यांचा भागाकार करून मिळत असतील, तर y² = x³ + ax² + bx + c या समीकरणाने एक ‘एलिप्टिक कर्व्ह’ (elliptic curve) निर्धारित होतो. उदाहरणार्थ, y² = x³ - 1 हा एलिप्टिक कर्व्ह आपण कॅटलानच्या अनुमानासंबंधात विचारात घेतला होता, आणि फक्त y = 3 व x = 2 याच नैसर्गिक संख्या हे समीकरण संपन्न करतात असे पाहिले होते. तसेच y² = x³ – x² + ¼ हे समीकरण देखील एक एलिप्टिक कर्व्ह निर्धारित करते. (एलिप्टिक कर्व्ह आणि आपण भूमितीत शिकतो ते लंबवर्तुळ यांचा संबंध दूरान्वयानेच लागतो.) प्रत्येक एलिप्टिक कर्व्ह एका खास प्रकारच्या फलनाशी संबंधित असला पाहिजे असे तानियामा व शिमुरा यांचे अनुमान सांगते. अशा फलनाला ‘मॉड्युलर फॉर्म’ असे म्हणतात, आणि म्हणून या अनुमानाचे नाव आहे ‘मॉड्युलॅरिटी अनुमान’ (Modularity Conjecture).

तीस वर्षे लोटल्यानंतर १९८६च्या सुमारास गेरहार्ड फ्राय (Gerhard Frey), ज्याँ-पिएर सेर (Jean-Pierre Serre) आणि केन रिबेट (Ken Ribet) या गणितज्ञांनी असे लक्षात आणून दिले की जर फर्माचे विधान खोटे असेल, म्हणजे xⁿ + yⁿ = zⁿ या समीकरणाचे एखादे उत्तर n या दोनपेक्षा मोठ्या संख्येसाठी मिळत असेल, तर आपल्याला मॉड्युलर नसलेला एक एलिप्टिक कर्व्ह लिहिता येइल, म्हणजेच मॉड्युलॅरिटी अनुमान खोटे पडेल. याचाच अर्थ असा की जर मॉड्युलॅरिटी अनुमान सिद्ध केले तर फर्माचे विधानही सिद्ध होईल. या गहन संबंधामुळे काही गणितज्ञ मॉड्युलॅरिटी अनुमान सिद्ध करण्याकडे नव्याने आकर्षित झाले. त्यांपैकी एक होते अमेरिकेतील प्रिन्स्टन विद्यापीठातील प्राध्यापक अँड्रयू वाइल्स (Andrew Wiles). वयाच्या दहाव्या वर्षापासून त्यांना फर्माच्या विधानाने आकर्षून घेतले होते. त्यांची मनोमन तीव्र इच्छा होती की तीनशे वर्षांत कुणाला सिद्ध न करता आलेले हे विधान आपणच सर्वप्रथम सिद्ध करावे. पण मार्ग दिसत नव्हता. आता मॉड्युलॅरिटी अनुमान त्यांना खुणावत होते. शिवाय हे अनुमान गणिताच्या मुख्य प्रवाहाचा भाग असल्याने तिकडे मोर्चा वळवणे सर्व दृष्टींनी हितकारक होते.

दुसऱ्या कुठल्याही प्रश्नाचा विचारही न करता सर्व लक्ष फर्माच्या विधानावर केंद्रित करायचे वाइल्स यांनी ठरवले खरे, पण त्याबरोबर काही दंडकही घालून घेतले. सर्वात महत्त्वाचा म्हणजे आपले काम पूर्णतः गुप्त राखायचे हा. उच्च स्तरातील गणितज्ञांमध्ये सामान्यतः सहकाराची आणि विचारांचे आदान-प्रदान करण्याची प्रथा असते. मग गुप्तता का पाळायची? गुप्तता पाळली म्हणजे आपले लक्ष विचलित होणार नाही, इतरांच्या नजरांचा दबाव पडणार नाही, हे सगळे खरे असले तरी आपण मिळवत असलेली उत्तरे इतरांना कळू नयेत हा देखील वाइल्सचा उद्देश असणार, कारण इतरांनी आपल्या आधी बाजी मारली तर सगळे श्रेय त्यांनाच मिळेल! आपला प्रकल्प लांब पल्ल्याचा असणार आणि त्या काळात आपण कोणतेच शोधनिबंध लिहू शकणार नाही याची कल्पना असल्यामुळे आपण याआधी केलेल्या चांगल्या संशोधनावर आधारलेले पण अद्याप प्रसिद्ध न केलेले निबंध वाइल्स प्रसिद्धीस देत राहिले, जेणेकरून कुणाला शंकाही येऊ नये, हा प्राणी सध्या काय करतोय याची. वाइल्ससारखे अगदी थोडे गणितज्ञ सोडले तर बऱ्याच जणांची खात्री होती की मॉड्युलॅरिटी अनुमान सिद्ध करणे अशक्य कोटीतले आहे, आणि म्हणून ते त्याच्या वाटेलाही जात नसत. ही गोष्ट वाइल्सच्या दृष्टीने फायद्याचीच ठरत होती.

वाइल्स जरूरीपुरतेच प्रिन्स्टन विद्यापीठाच्या गणित विभागात जात असत. बाकी सदासर्वदा आपल्या घरातील छपरालगतच्या खोलीत (attic) त्यांचे काम अव्याहतपणे चालू असे. वेगवेगळे दृष्टिकोन, वेगवेगळी तंत्रे वापरत ते तब्बल सहा वर्षे झुंजत राहिले. दरम्यानच्या काळात त्यांनी आपली मैत्रिण नाडा हिच्याशी विवाह केला, त्यांना दोन मुलीही झाल्या. त्यांच्याबरोबर गमतीचे चार शब्द दिवसाकाठी बोलणे हाच त्यांचा विरंगुळा होता. पण तो जरूरीचा होता. वाइल्सच्या प्रयत्नांना यश येत गेले. खडक फोडून मिळवाव्यात अशा मोलाच्या निष्पत्ती एकामागून एक त्यांच्या वाट्याला आल्या. पण हे कुणाकडे बोलायची सोय नव्हती. आपले झगडे आणि आपल्या उपलब्धी आपल्यातच जिरवाव्या लागत होत्या. मॉड्युलॅरिटी अनुमान सिद्ध करण्यासाठी एलिप्टिक कर्व्हजचे कितीतरी प्रकार त्यांना हाताळावे लागले. त्यात बऱ्याच परिगणना (calculations) कराव्या लागल्या. त्या एकूण-एक सगळ्या बरोबर आहेत हे कोणीतरी तपासावे असे त्यांना वाटले. शेवटी प्रिन्स्टन विद्यापीठातील त्यांचे सहकारी प्राध्यापक निक काट्झ यांना विश्वासात घ्यायचे ठरवले. काट्झनी तपासायचे मान्य केले, पण ती काही साधीसोपी वाइल्सच्या ऑफिसमध्ये बसून करायची गोष्ट नव्हती. यातून मार्ग काढण्यासाठी वाइल्सनी प्रिन्स्टन विद्यापीठातील पदव्युत्तर विद्यार्थ्यांकरता एक कोर्स देऊ केला. त्याचे शीर्षक होते ‘एलिप्टिक कर्व्हजसंबंधी परिगणन’ (Calculations on Elliptic Curves). काही विद्यार्थी आणि काट्झ उपस्थित राहू लागले. वाइल्स फळ्यावर सर्व तपशील उलगडून दाखवायचे आणि काट्झ ते सगळे तपासायचे. पण हे परिगणन कशासाठी चालले आहे याची सुतराम कल्पना नसल्याने विद्यार्थ्यांचा उत्साह मावळत गेला, आणि एकेक करून ते यायचे थांबले. ही स्थिती वाइल्स आणि काट्झ यांच्या पथ्यावरच पडली.

असे तावून सुलाखून निघाल्यावर आपला पराक्रम जाहीर करायची वेळ आली आहे असे वाइल्सनी मनात आणले. सनई-चौघडे वाजवून तसे न करता त्यांनी एका परिषदेमध्ये तीन व्याख्याने देण्यासाठी वेळ मागून घेतला. इंग्लंडमधील केंब्रिज विद्यापीठातील आयझॅक न्यूटन संस्थेत ही परिषद जून १९९३ मध्ये भरली. वाइल्सच्या व्याख्यानमालिकेचे नाव होते ‘एलिप्टिक कर्व्हज, मॉड्युलर फॉर्मस आणि गालवा रिप्रेझेंटेशन्स’ (Modular Forms, Elliptic Curves and Galois Representations). केंब्रिजला आल्यावर वाइल्सनी आपले हस्तलिखित बॅरी मेझर (Barry Mazur) या हार्वर्ड विद्यापीठातील एका ज्येष्ठ प्राध्यापकांकडे नजर टाकण्यासाठी सोपवले. ते बघताच मेझरसाहेब आश्चर्याने स्तब्ध झाले. वाइल्स काय बोलणार आहे याचा काट्झ व मेझर यांच्याशिवाय कुणालाही सुगावा लागला नव्हता. पहिले व्याख्यान ऐकल्यानंतर काही गणितज्ञांना हे काय प्रकरण चालले आहे याची अंधुकशी कल्पना येऊ लागली. जगातील अनेक संस्थांच्या गणित विभागांकडे इमेल्स जाऊ लागल्या. दुसऱ्या व्याख्यानानंतर उत्सुकता शिगेला पोहोचली. तरीही वाइल्स स्पष्टपणे फर्माच्या विधानाचा उल्लेखही करत नव्हते. तिसऱ्या व्याख्यानाच्या आधी मात्र काही सुज्ञ लोकांनी हॉलमधील मोक्याच्या जागा पटकावल्या होत्या. फर्माचे विधान सिद्ध झाल्याची घोषणा होत असलेल्या, या शतकांमध्ये क्वचित घडणाऱ्या घटनेचे आपण जवळून साक्षी असावे हा हेतु. फर्माचे विधान सिद्ध करायला मॉड्युलॅरिटी अनुमानाचा जो भाग आवश्यक होता त्याची सिद्धता कशी द्यायची हे दाखवल्यावर व्याख्यानाच्या अखेरीस वाइल्सनी फक्त फर्माचे विधान फळ्यावर लिहिले आणि ते म्हणाले, ‘मला वाटते मी आता थांबावे’.

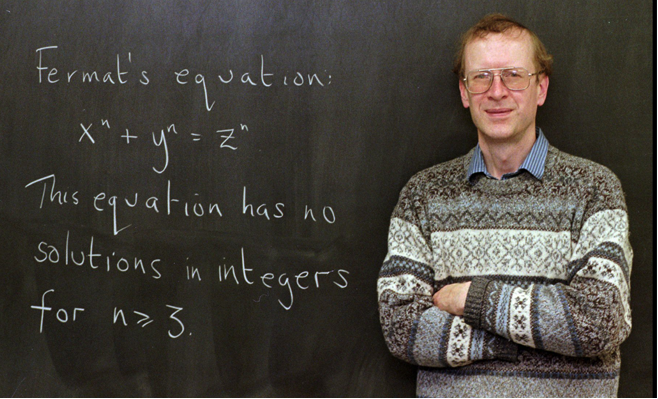
फर्माचे विधान आणि अँड्रयू वाइल्स

टाळ्यांचा कडकडाट झाला. संस्थेच्या निदेशकांनी आणलेली शॅम्पेनची बाटली उघडल्याचा आवाज आला. छायाचित्रे लखलखली. दुसऱ्या दिवशी (२४ जून १९९३) न्यू यॉर्क टाइम्सच्या पहिल्या पानावर मथळा होता: ‘अखेरीस, गणितातील दीर्घकालीन कोड्याचे उत्तर सापडले’ (At last, Shout of Eureka! In Age-old Math Mystery).

न्यू यॉर्क टाइम्समधील मथळा, २४ जून १९९३

लवकरच वाइल्सचा ‘वर्षातील सर्वात जास्त विलक्षण असणाऱ्या पंचवीस जणांमध्ये (The 25 Most Intriguing People of the Year) समावेश झाला. इतकेच काय, पुरुषांचे कपडे बनवणाऱ्या एका कंपनीने वाइल्सकडून पुष्टी (endorsement) मागितली!

गणितातील प्रमेयाची सिद्धता परिषदेत व्याख्यान देऊन भागवता येत नाही. ती एका शोधनिबंधात सविस्तरपणे आणि बिनचूकपणे लिहून एखाद्या शास्त्रीय ज्ञानपत्रिकेकडे पाठवावी लागते. वाइल्सनी आपला दोनशे पानी शोधनिबंध ‘गणितातील नवे शोध’ (Inventiones mathematicae) या प्रख्यात जर्नलकडे पाठवला. त्याचे संपादक होते बॅरी मेझर. नेहमीप्रमाणे दोन किंवा तीन परीक्षक न नेमता, त्यांनी वाइल्सच्या शोधनिबंधाचे सहा भाग करून सहा परीक्षकांकडे पाठवले. त्यांना स्पष्टीकरणासाठी वाइल्सशी संपर्क साधण्याची मुभा दिली. आता वाइल्सना घरी जाऊन परीक्षकांच्या निर्वाळ्याची वाट बघणे क्रमप्राप्त होते. आपले काम दोनदोनदा तपासून पाहिले असल्याने काही किरकोळ चिह्नपद्धतीसंबंधीच्या (notation) किंवा नजरचुकीने झालेल्या गोष्टी सोडल्या तर बाकी सर्व गोष्टी ठीकच असा वाइल्सना विश्वास होता. सुरुवातीला तसेच झाले. वाइल्स परीक्षकांच्या शंकांचे तत्काळ निराकरण करत गेले.

सहा परीक्षकांपैकी एक होते निक काट्झ. त्यांनी पूर्वीच वाइल्सबरोबर एलिप्टिक कर्व्हजच्या बाबतीतील परिगणना तपासल्या होत्या. त्यांच्याकडे तेच सत्तर पानी प्रकरण आले होते. आता मात्र कुठलीही सिद्धता ‘ठीकच असणार’ असे मानून चालणार नव्हते. त्यांच्याही गणिती ख्यातीची ही एक परीक्षा होती. ते डोळ्यात तेल घालून बारकाईने प्रत्येक युक्तिवाद समजून घेत होते. वाइल्स ईमेलने किंवा फॅक्सने त्यांना उत्तरे पुरवत होते. काही महिन्यांनी, सप्टेंबर १९९४ मध्ये, एका निर्णायक स्वरूपाच्या बाबीत वाइल्सना त्यांचे समाधान करता आले नाही. जास्त विचारांती दोघांनाही कळून चुकले की ती एक छोटीशी चूक नसून युक्तिवादातील सूक्ष्म पण मूलभूत उणीव होती. दोघांनाही आश्चर्य वाटून राहिले की ती आधी त्यांच्या नजरेतून कशी सुटली. आता ती दुरुस्त केल्याखेरीज गत्यंतर नव्हते.

अँड्रयू वाइल्सनी आकाश-पाताळ एक केले, पण त्यांना सिद्धतेतील त्रुटी भरून काढता येईना. हाता-तोंडाशी आलेला घास गळून पडायची पाळी आली. ह्या परिस्थतीची माहिती फक्त त्या जर्नलचे संपादक आणि वाइल्सच्या शोधनिबंधाचे परीक्षक यांनाच होती. तरी इतरांना काहीतरी अनपेक्षित घटत असल्याची कुणकुण लागत होती. शेवटी डिसेंबरच्या सुरुवातीला वाइल्सने ईमेलद्वारे सद्यःस्थितीची इतरांना कल्पना दिली आणि लवकरच उर्वरित काम पुरे होईल असा विश्वास प्रकट केला. पण गणिती समाजाचे समाधान झाले नाही. ज्यांनी जून महिन्यात वाइल्सच्या संयमित पण जाहीर निवेदनाचे उत्साहाने स्वागत केले होते, त्यांपैकीच काही जण आता म्हणू लागले की चुकीची तर चुकीची, पण काय सिद्धता आहे ते आम्हाला कळू तरी द्या. वाइल्सना तसे बिलकुल करायचे नव्हते. कारण मग खूप जणांनी चूक सुधारायचा प्रयत्न केला असता, व जो कोणी सर्वात आधी यशस्वी होईल त्याला श्रेय मिळून गेले असते. पर्वतारोहणात जसे जो पहिल्यांदा शिखरावर पाय ठेवतो त्यानेच ते काबीज केले असे होते, तसेच गणिती दुनियेतसुद्धा किती जणांनी केवढे काम आधी करून ठेवले होते याचा फारसा विचार होत नाही, तर सिद्धतेचा शेवटचा दुवा जोडून देणाऱ्याच्याच नावाने ते प्रमेय ओळखले जाते. सात वर्षे सतत तहान-भूक विसरून केलेले काम दुसऱ्या कोणाला आयते सुपूर्द करायची वाइल्सची तयारी नव्हती. शिवाय एकदा का त्यांनी आपण काय केले आहे ते मुक्तपणे सांगून टाकले की त्यांना अनेक शंकाकुशंकांना तोंड द्यावे लागले असते, व त्यांचा स्वतःचा दुरुस्तीचा प्रयत्न लांब राहिला असता. एकीकडे त्यांच्यावरचा दबाव दिवसेंदिवस वाढत होता, व दुसरीकडे दुरुस्ती जमत नव्हती.

शेवटी वाइल्सने प्रिन्स्टन विद्यापीठातील आपला मित्र पीटर सारनाक (Peter Sarnak) याच्याजवळ कबूल केले की ते पराजय पत्करायच्या मार्गावर आहेत. ते दोघे जवळपास एकाच वेळी प्रिन्स्टनला आले होते. या मित्राने सुचवल्यावरून वाइल्सनी रिचर्ड टेलर या केम्ब्रिज विद्यापीठातील गणितज्ञाला विश्वासात घ्यायचे ठरवले. त्याने १९८८ साली वाइल्सच्याच मार्गदर्शनाखाली प्रिन्स्टन विद्यापीठात पीएच. डी. केली होती. वाइल्सचा शोधनिबंध तपासत असलेल्या सहा जणांत तोही होता. जानेवारी १९९४ पासून दोघांनी ‘पुनश्च हरि ओम’ म्हणत वाइल्सच्या सिद्धतेचा पुरा आराखडा तपासणे सुरु केले. आधी सोडून दिलेले मार्ग परत चोखाळायचा प्रयत्न केला, जेणेकरून निक काट्झने दाखवलेली फट भरून निघेल.

रिचर्ड टेलर, १९९९

तेवढ्यात १९९४ सालच्या एप्रिल महिन्याच्या सुरुवातीला कित्येक जणांच्या संगणकांवर हान्री डार्मो (Henri Darmon), प्रिन्स्टन विद्यापीठ, या नावे एक इमेल आली. त्यात लिहिले होते की नोॲम एल्किस (Noam Elkies) यांना फर्माच्या विधानाविरुद्ध एक उदाहरण मिळाले आहे. त्यांनी एक 1020 पेक्षा मोठी मूळ संख्या n शोधली आहे, आणि x, y आणि z अशा नैसर्गिक संख्या त्यांना सापडल्या आहेत की ज्यांनी xⁿ + yⁿ = zⁿ हे समीकरण संपन्न होते. संपले, सगळेच मुसळ केरात गेले म्हणायचे. सहा वर्षांपूर्वी हार्वर्ड विद्यापीठातील याच प्राध्यापक एल्किस यांनी एक उदाहरण देऊन ऑयलरने १७६९ मध्ये केलेले एक अनुमान खोटे ठरवले होते. ऑयलरचे म्हणणे होते की x, y, z आणि w अशा कुठल्याही नैसर्गिक संख्यांनी x⁴ + y⁴ + z⁴ = w⁴ हे समीकरण साध्य होणे शक्य नाही. दोनशे वर्षे हे अनुमान ना कुणी सिद्ध करू शकले ना खोटे ठरवू शकले. पण १९८८ साली एल्किस यांनी

हे प्रत्युदाहरण (counterexample). अशी अनंत प्रत्युदाहरणे मिळवायची एक पद्धती त्यांनी दाखवली. त्यांना मिळालेले हे त्यांतल्या त्यात लहान प्रत्युदाहरण होते. त्याच वर्षी एल्किस यांचे तंत्र वापरून रॉजर फ्राय यांनी संगणकाच्या साह्याने सर्वात लहान प्रत्युदाहरण मिळवले. ते होते

यातील आकडे किती अवाढव्य आहेत, पण यांपेक्षा लहान आकड्यांनी ऑयलरचे समीकरण साध्य होत नाही. गणिती लोक तर्काच्या कसोटीवर उतरणाऱ्या सिद्धतेचा का आग्रह धरतात हे यावरून स्पष्ट होते. आता एल्किस जर फर्माच्या विधानासाठी प्रत्युदाहरण देत असले, तर वाइल्सला त्याची ‘सिद्धता’ दुरुस्त करता येणारच नाही, कारण फर्माचे विधानच खोटे ठरले जाते! या इमेलने खळबळ माजली, पण थोडा काळच, कारण तिच्यावरची सुरुवातीची तारीख होती एक एप्रिल! ही वाइल्सची क्रूर चेष्टा ठरली होती, पण त्यांच्या मागचा तगादा कमी झाला नव्हता. जणू ‘बाप दाखव नाहीतर श्राद्ध कर’ असे गणिती लोक म्हणत होते.

१९९४ सालचा सप्टेंबर उजाडला तरी बोगद्याच्या शेवटाचा प्रकाश दिसत नव्हता. लहानपणच्या गोड स्वप्नाचे एका दुःस्वप्नात रूपांतर होत होते. वाइल्सनी हार मानून आपली फर्माच्या विधानाची अपूर्ण सिद्धता गणितज्ञांना उपलब्ध करून द्यायचे ठरवले. सगळा प्रवास काही वाया गेलेला नाही, फर्माचे विधान सिद्ध करण्यात आपण भरघोस प्रगती तरी नक्कीच केली आहे अशी स्वतःची समजूत घालायला वाइल्सनी सुरुवात केली. पण रिचर्ड टेलरने केम्ब्रिजला परतण्यापूर्वी महिनाभर चिकाटीने काम चालू ठेवले. तीन वर्षांपासून अवलंबलेला नवा मार्ग नेमका कुठल्या खाईत लुप्त होतो आहे हे तरी पाहू या, या सामान्य उद्देशाने विचार करत असताना वाइल्सला अचानक दिसून आले की जुना मार्ग आणि नवा मार्ग यांपैकी कोणत्याच मार्गाने पुढे जाता येत नसले तरी दोन्हीची गुंफण करता येतीय. निक काट्झने दाखवलेली फट भरून काढता आली नाही तरी तिला बगल देता येईल (circumvent)!

एका प्रेरकशक्तीने भारलेल्या क्षणी हा साक्षात्कार झाला होता. हा दोन मार्गांचा संयोग इतके महिने कसा ध्यानात आला नाही याचा त्यांना अचंबा वाटला. पण ही वेळ आश्चर्य करत राहण्याची नव्हती. तरीही एक रात्र वाइल्सनी तशीच जाऊ दिली. दुसऱ्या दिवशी छपराजवळच्या खोलीतून खाली येऊन ते पत्नीला – नाडाला - म्हणाले, ‘मला ते मिळालंय, मला वाटतं मला ते सापडलंय’. नाडाला वाटले ते त्यांच्या लहान मुलीच्या हरवलेल्या खेळण्याबद्दल बोलत आहेत. वाइल्स म्हणाले, ‘खेळणे नाही, फर्माचे फर्मान!’ नाडाचा वाढदिवस ऑक्टोबर महिन्यात असतो. गेल्या वर्षी सप्टेंबर महिन्यात वाइल्स निराशेच्या गर्तेत असताना ती म्हणाली होती की तिला वाढदिवसाची एकच भेट हवी आहे, ती म्हणजे फर्माच्या विधानाची बिनचूक सिद्धता. पण ती भेट वाइल्स देऊ शकले नव्हते. यंदा वाढदिवसाच्या दिवशी त्यांनी नाडाच्या हातात परिपूर्ण शोधनिबंधाची प्रत ठेवली. आठ वर्षांच्या निरलस व व्यापक कामाचे ते फळ होते. फर्माच्या विधानाने गणितज्ञांना दिलेली शेवटची हुलकावणी संपली होती.

सिद्धतेसाठी नव्याने वापरलेली पद्धत जास्त सुटसुटीत होती, पृष्ठसंख्या दोनशेवरून दीडशेच्या आत आली. वाइल्सनी त्यांच्या संशोधनाची दोन शोधनिबंधात विभागणी केली: पहिला, मोठा स्वतःच्या नावावर आणि दुसरा, छोटा पण निर्णायक, स्वतःच्या व रिचर्ड टेलर या दोघांच्या नावांवर. ऑक्टोबर १९९४ च्या मध्याला दोन्ही शोधनिबंध ॲनल्स ऑफ मॅथेमॅटिक्स या अत्युत्कृष्ट ज्ञानपत्रिकेकडे रवाना झाले. ते दोन्ही १९९५ मध्ये पाठोपाठ प्रसिद्ध झाले. त्यांमध्ये तानियामा व शिमुरा यांचे मॉड्युलॅरिटी अनुमान फक्त काही प्रकारच्या एलिप्टिक कर्व्हजसाठी, सेमिस्टेबल कर्व्हजसाठी, सिद्ध केले होते. तेवढे फर्माचे विधान सिद्ध करायला पुरेसे होते. त्यानंतरच्या चार-पाच वर्षांत इतर गणितज्ञांनी तानियामा व शिमुरा यांचे मॉड्युलॅरिटी अनुमान पूर्णतः सिद्ध केले. विसाव्या शतकातील गणिती शोधनिबंधांत अँड्रयू वाइल्स यांचा शोधनिबंध सर्वात महत्त्वाचा मानला जातो. ‘लँगलँडस प्रोग्रॅम’ (Langland’s Program) हा गणितातील दोन अगदी भिन्न शाखांत एकसूत्रता आणून देणारा, एकमेकांत सेतू बांधून देणारा महत्त्वाकांक्षी प्रकल्प आहे. वाइल्सनी प्रथम उपयोगात आणलेल्या तंत्रांचा वापर या प्रकल्पातील विविध सेतू बांधण्यासाठी झाला आहे, अजूनही होत आहे. इतकेच नव्हे तर, आता या प्रकल्पाच्या पलीकडचे धागेदोरे शोधण्यात जगातील उत्तमोत्तम गणिती मग्न आहेत. वाइल्सनी आपला शोधनिबंध पत्नीला आणि तीन मुलींना अर्पण केला आहे. स्वतः लिहिलेले पुस्तक कुणाला तरी अर्पण करण्याची सर्वसामान्य रीत आहे. कधी कधी आपल्या दिवंगत मार्गदर्शकाला किंवा सहकाऱ्याला शोधनिबंध अर्पण केल्याचे आढळते. मात्र अँड्रयू वाइल्सच्या शोधनिबंधाचे समर्पण बोलके आहे.

अंकशास्त्रज्ञ तरलोक शोरी या माझ्या मित्राने मला १९९५ साली पाठवलेल्या बातमीवजा इमेलनंतर जवळजवळ तीन वर्षांनी एका शुक्रवारच्या संध्याकाळी माझ्या पत्रपेटीत मला एक छोटेखानी पुस्तक मिळाले. ते तरलोकनेच पाठवले होते, सायमन सिंग (Simon Singh) याने लिहिलेले, ‘फर्माचे रहस्य’ (Fermat’s Enigma) या शीर्षकाचे.

माझा वाचनाचा वेग खूप कमी असूनही ते तीनशे पानी पुस्तक मी रविवारपर्यंत वाचून संपवले. तरलोकला आभारप्रदर्शक लांबलचक इमेल पाठवली. त्यानंतर माझी पत्नी निर्मला आणि माझे मित्र, मग ते गणिती असोत वा नसोत, सगळ्यांनी त्या पुस्तकाची किती पारायणे केली असतील ते मोजवत नाही. त्यात अंतर्भूत केलेल्या गोष्टी जास्त रोचक आहेत की लिहिण्याची शैली जास्त खुसखुशीत आहे ते सांगणे कठीण आहे.

(पुढील भाग)
---

बालमोहन लिमये

(balmohan.limaye@gmail.com)



लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.

बालमोहन लिमये यांचे इतर लिखाण