पायथागोरसचे प्रमेय - भाग २
पायथागोरसचे प्रमेय
(मी शाळेत न शिकलेले पण आय. आय. टी.त शिकवलेले)
बालमोहन लिमये
https://aisiakshare.com/node/8508 हे लेख नंदा खरे यांच्या स्मृतीला अर्पण, ज्यांनी मला लिहिते केले. भाग २ पहिल्या भागात पाहिलेले पायथागोरसचे प्रमेय आयताच्या किंवा काटकोन त्रिकोणाच्या कर्णासंबंधी आहे. या दोन्ही आकृती दोन मिती (dimension) असलेल्या प्रतलावर (on a plane) काढता येतात. या द्विमितीय प्रमेयाची तीन मिती असलेल्या अवकाशात दोन वेगवेगळी प्रतिरूपे (analogues) होऊ शकतात, एक लांबीची संकल्पना विचारात घेऊन आणि दुसरे क्षेत्रफळाची संकल्पना विचारात घेऊन. आमच्या काळी तीन मितीच्या अवकाशातील भूमिती महाविद्यालयीन गणिताचा एक भाग होता. तिला घन भूमिती (Solid Geometry) असे म्हणत. मात्र या त्रिमितीय प्रतिरूपांपैकी कोणतेच आमच्या वाट्याला आले नाही. ती प्रतिरूपे आमच्या अभ्यासक्रमात नव्हती हे खरे, पण ज्यांना पायथागोरसचे द्विमितीय प्रमेय नीट समजले आहे, त्यांना ती सहज उमजली असती व उद्बोधकही वाटली असती. या दोन प्रतिरूपांचा काही अन्योन्य संबंध असू शकतो का याची उकल मात्र मला अजून झालेली नाही. पायथागोरसचे त्रिमितीय प्रमेय अवकाशात आयताचे प्रतिरूप म्हणजे आयताकृती पेटी (rectangular box). ती घनासारखी (cube) दिसते म्हणून तिला घनाभ (cuboid) असे म्हणतात. घनाभाच्या आयताकारी सहा फलकांपैकी प्रत्येक फलकावर दोन कर्ण (face diagonals) काढता येतात. त्यांपैकी समोरासमोरील फलकांवरच्या चार कर्णांची लांबी समान असते. या शिवाय घनाभाच्या आठ शिरोबिंदूंपैकी एकाच फलकात नसलेले दोन शिरोबिंदू जोडून चार अवकाश कर्ण (space diagonals) देखील काढता येतात. त्या सर्वांची लांबी समान असते. अवकाशातील पायथागोरसचे प्रमेय सांगते की घनाभाच्या अवकाश कर्णाच्या लांबीचा वर्ग हा घनाभाच्या लांबी, रुंदी व उंची यांच्या वर्गांच्या बेरीजेइतका असतो.

वरील आकृतीतील घनाभाची a, b, c अशी लांबी, रुंदी, उंची अनुक्रमे नारिंगी, निळसर व हिरवा या रंगांनी काढलेल्या कडांनी दाखवली आहे. तसेच त्याच्या अवकाश कर्णाची लांबी d तुटक निळ्या रेषेने दाखवली आहे, आणि a लांबी व b रुंदी असलेल्या घनाभाच्या आयताकृती फलकाच्या कर्णाची लांबी p तुटक तांबड्या रेषेने दाखवली आहे. या आयतासाठी पायथागोरसचे प्रमेय वापरून आपल्याला a2 + b2 = p2 असे समीकरण मिळते. आता हिरव्या रंगाने दाखवलेली c लांबीची कडा नारिंगी आणि निळसर या रंगांनी दाखवलेल्या a आणि b लांबीच्या दोन्ही कडांशी काटकोन करत असल्याने ती p लांबीच्या कर्णाशीही काटकोन करते. या p आणि c लांबीच्या बाजू असलेल्या काटकोन त्रिकोणाच्या कर्णाची लांबी आहे d. परत एकदा पायथागोरसचे प्रमेय वापरून आपल्याला p2 + c2 = d2 असे समीकरण मिळते. ही दोन समीकरणे एकत्र केली की आपल्याला a2 + b2 + c2 = p2 + c2 = d2 हे हवे असलेले समीकरण मिळवता येते. 'द ग्वा'चे प्रमेय आता चौकोनांऐवजी त्रिकोणांचा विचार करू या. अवकाशात त्रिकोणाचा समधर्मी म्हणजे चतुष्फलक (tetrahedron). त्याचे चारही फलक (faces) म्हणजे पृष्ठभाग त्रिकोणी असतात. इजिप्तमधील पिरॅमिडचे बाहेरून दिसणारे चारही फलक त्रिकोणी असले तरी त्याला एक पाचवा फलक असतो, तो म्हणजे त्याचा चौकोनी पायथा; म्हणून तो पिरॅमिड काही चतुष्फलक नाही. आपण चतुष्फलकाला त्रिकोणी मेरु (triangular pyramid) म्हणू शकतो. त्याच्या चार शिरोबिंदूंपैकी (vertices) प्रत्येक शिरोबिंदूशी तीन कडा (edges) येऊन मिळतात. जर एखाद्या चतुष्फलकाच्या एका शिरोबिंदूशी मिळणाऱ्या तिन्ही कडा एकमेकींशी काटकोन करत असतील तर त्याला काटकोन त्रिकोणी चतुष्फलक म्हणायचे. उदाहरणार्थ, एका आयताकार पेटीचा एक छोटा कोपरा करवतीने तिरका कापून काढला तर काटकोन त्रिकोणी चतुष्फलक मिळू शकतो. खालील आकृतीत चतुष्फलकाच्या एका शिरोबिंदूशी मिळणाऱ्या तिन्ही कडा एकमेकींशी कशा काटकोन करतात ते दाखवले आहे; तो शिरोबिंदू असणारे तीन काटकोन त्रिकोणी फलक दिसत आहेत, पण त्या शिरोबिंदूसमोरचा फलक दृष्टिआड आहे.
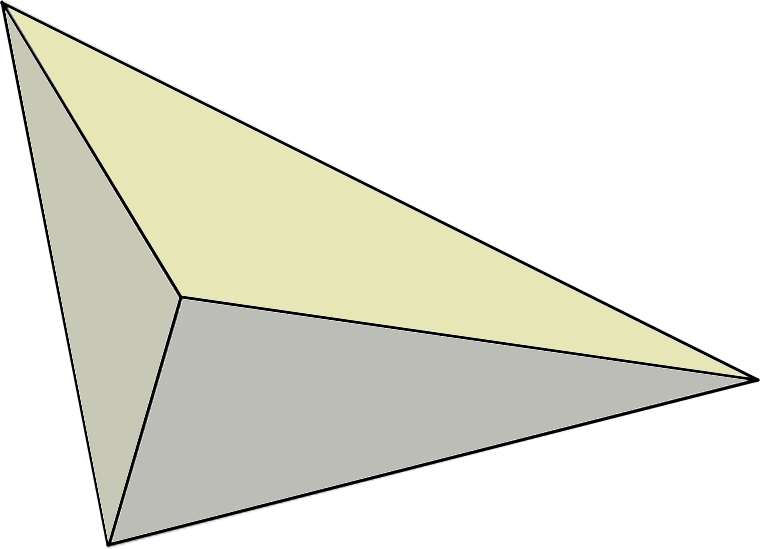
काटकोन त्रिकोणी चतुष्फलक
पायथागोरसच्या प्रमेयाप्रमाणेच द ग्वा (de Gua) या फ्रेंच गणितज्ञाच्या नावाने ओळखले जाणारे प्रमेय सांगते की काटकोन त्रिकोणी चतुष्फलकातील ज्या शिरोबिंदूशी तिन्ही कडा काटकोनात असतात त्याच्या समोरील फलकाच्या क्षेत्रफळाचा वर्ग हा इतर तीन फलकांच्या क्षेत्रफळांच्या वर्गांच्या बेरीजेइतका असतो. खरे म्हणजे द ग्वाच्या आधी योहान फाउलहाबर (Johann Foulhaber) या जर्मन गणितज्ञाला ते प्रमेय सोळाव्या शतकातच अवगत होते (Modern Pure Solid Geometry, by N. Altschiller-Court, New York, p. 300). पायथागोरसचे प्रमेय वापरून आपण ते सिद्ध करू या.
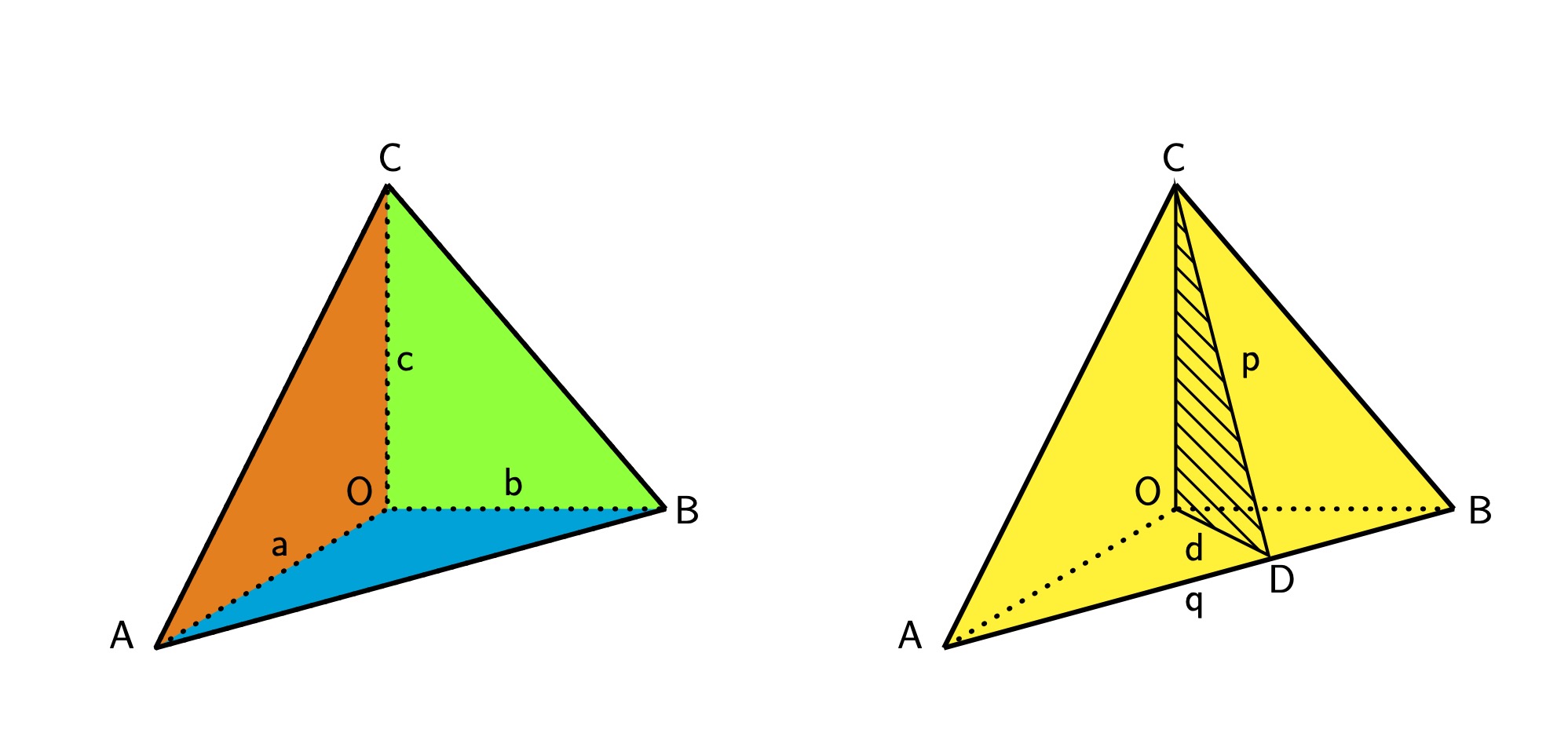
काटकोन त्रिकोणी चतुष्फलक
वरीलपैकी पहिल्या आकृतीमध्ये O, A, B, C हे एका काटकोन त्रिकोणी चतुष्फलकाचे शिरोबिंदू आहेत. त्यातील O ह्या शिरोबिंदूशी मिळणाऱ्या तिन्ही कडा एकमेकींशी काटकोन करतात. समजा या तीन कडांच्या लांबी a, b, c आहेत. मग O हा शिरोबिंदू असणाऱ्या, निळसर, हिरवा व नारिंगी या रंगांनी दाखवलेल्या, काटकोन त्रिकोणी फलकांची क्षेत्रफळे अनुक्रमे ab/2, bc/2, ca/2 अशी होतील, व म्हणून त्यांचे वर्ग होतील a2b2/4, b2c2/4, c2a2/4 असे. शेजारील आकृतीत OC ह्या कडेतून जाणारे व AB ह्या कडेला लंब असलेले प्रतल आपल्या चतुष्फलकाला OCD ह्या काटकोन त्रिकोणात छेदताना दाखवले आहे. या प्रतलावरील प्रत्येक सरळ रेषा AB या सरळ रेषेशी काटकोन करते, व म्हणून CD आणि AB या रेषा काटकोनात आहेत. OD, CD, AB या रेषांच्या लांबी अनुक्रमे d, p, q अशा दाखवल्या आहेत. आता O या शिरोबिंदूसमोरील ABC ह्या पिवळ्या रंगाने दाखवलेल्या त्रिकोणी फलकाचे क्षेत्रफळ आहे pq/2, व म्हणून त्याचा वर्ग आहे p2q2/4. पण OCD ह्या काटकोन त्रिकोणासाठी पायथागोरसचे प्रमेय वापरून p2 = c2 + d2 असे समीकरण मिळते. तसेच OAB ह्या काटकोन त्रिकोणासाठी पायथागोरसचे प्रमेय वापरून q2 = a2 + b2 असे समीकरण मिळते, आणि त्याच काटकोन त्रिकोणासाठी पायथागोरसचे व्युत्क्रमी प्रमेय वापरून d2 = a2b2/(a2 + b2) असे समीकरण मिळते. या तिन्ही समीकरणाच्या साह्याने p2q2/4 = (c2 + d2)(a2 + b2)/4 = (a2b2 + b2c2 + c2a2)/4 हे हवे असलेले उत्तर सहज मिळून जाते. पायथागोरसची चतुष्के (Pythagorean Quadruples) पुन्हा थोडे अंकशास्त्रात शिरू या. पायथागोरसच्या त्रिमितीय प्रमेयानुसार, जर एका घनाभाची लांबी, रुंदी, उंची a, b, c अशी असेल, व त्याच्या अवकाश कर्णाची लांबी d असेल तर तर a2 + b2 + c2 = d2, म्हणजे a2 + b2 + c2 या संख्येचे वर्गमूळ d असते, व तसेच द ग्वाच्या प्रमेयानुसार जर एका काटकोन त्रिकोणी चतुष्फलकातील फलकांची क्षेत्रफळे α, β, γ, δ अशी असतील व त्यांपैकी δ हे क्षेत्रफळ ज्या शिरोबिंदूशी तिन्ही कडा काटकोनात असतात त्याच्या समोरील फलकाचे असेल, तर α2 + β2 + γ2 = δ2, म्हणजे α2 + β2 + γ2 या संख्येचे वर्गमूळ δ असते. आता जर a, b, c किंवा α, β, γ या तिन्ही संख्या धन पूर्णांक असतील, तर d किंवा δ ही संख्यासुद्धा पूर्णांकच असेल असे काही नाही, जसे त्या तिन्ही संख्या 1 हा पूर्णांक असल्या तरी √ 3 हा काही पूर्णांक नाही. जर a, b, c, d हे चारही धन पूर्णांक असतील आणि d2 = a2 + b2 + c2 हे समीकरण साधत असेल, तर (a, b, c, d) या चौकडीला पायथागोरसचे चतुष्क (Pythagorean quadruple) असे म्हणतात. उदाहरणार्थ, (1, 2, 2, 3) हे पायथागोरसचे चतुष्क आहे, कारण 12 + 22 + 22 = 9 = 32. समजा (a, b, c, d) हे पायथागोरसचे चतुष्क आहे. मग (b, a, c, d) हे पण असणारच, कारण b2 + a2 + c2 = a2 + b2 + c2 = d2. तीच गोष्ट (c, b, a, d), (a, c, b, d) , (b, c, a, d) , (c, a, b, d) या चौकड्यांबाबत. परंतु ही चतुष्के काही वेगळी समजायला नकोत. तसेच p हा कुठलाही धन पूर्णांक असेल तर (pa, pb, pc, pd) हे देखील पायथागोरसचे चतुष्क असते, कारण (pa)2 + (pb)2 + (pc)2 = p2(a2 + b2 + c2) = p2d2 = (pd)2. परंतु हे नवे चतुष्क काही फारसे वेगळे नाही. ही पुनरावृत्ती टाळणे आवश्यक आहे. (a, b, c, d) या चतुष्कातील a, b, c या पूर्णांकांना 1 सोडून दुसऱ्या कोणत्याच पूर्णांकाने भाग जात नसेल, म्हणजे त्यांचा म. सा. वि. (g. c. d.) 1 असेल, तर त्या चतुष्काला आदिम चतुष्क असे म्हणू या. पायथागोरसची अनंत चतुष्के मिळवण्याचा एक मार्ग असा आहे. समजा a ही 1 पेक्षा मोठी कुठलीही विषम संख्या आहे, आणि a = 2k +1. मग b = 2k(k + 1) आणि c = 2k2 +2k +1 अशा संख्या घेतल्या तर (a, b, c) हे पायथागोरसचे आदिम त्रिक कसे मिळते हे आपण पाहिले आहे. या त्रिकातील c ही संख्या विषम असल्याने त्याच रीतीने दुसरे पायथागोरसचे आदिम त्रिक (c, d, e) आपण मिळवू शकतो. मग (a, b, d, e) हे पायथागोरसचे चतुष्क होते, कारण a2 + b2+ d2 = c2 + d2 = e2. आता e ही संख्यादेखील विषम असल्याने आपण आधीच्याच रीतीने तिसरे पायथागोरसचे आदिम त्रिक (e, f, g) मिळवले, तर (c, d, f, g) हे पायथागोरसचे चतुष्क होते, कारण c2 + d2+ f2 = e2 + f2 = g2. उदाहरणार्थ, (3, 4, 5) आणि (5, 12, 13) ही पायथागोरसची आदिम त्रिके आहेत, म्हणून (3, 4, 12, 13) हे पायथागोरसचे चतुष्क होते; तसेच (5, 12, 13) आणि (13, 84, 85) ही पायथागोरसची आदिम त्रिके आहेत, म्हणून (5, 12, 84, 85) हे पायथागोरसचे चतुष्क होते. ही कारवाई अशीच करत राहिलो तर आपल्याला पायथागोरसची अनंत चतुष्के मिळतात; ती सगळी आदिम असतात. मात्र या रीतीने सगळी आदिम चतुष्के मिळत नाहीत, जसे (1, 2, 2, 3) किंवा (3, 2, 6, 7). सगळी आदिम चतुष्के मिळवण्यासाठी युक्लिडने त्रिकांसाठी दिलेल्या सूत्रासारखेच एक वेगळे सूत्र आहे. जर (a, b, c, d) हे आदिम चतुष्क असेल, तर a, b, c यांपैकी एक तरी संख्या विषम असली पाहिजे. समजा a ही संख्या विषम आहे. आता m, n, p, q असे पूर्णांक घ्यायचे की m2 + n2 > p2 + q2 आणि nq > mp. मग a = m2 + n2 - p2 - q2, b = 2(nq - mp), c = 2(mq + np) या संख्या घेतल्या तर आपल्याला a2 + b2+ c2= (m2 + n2 + p2 + q2)2 असे समीकरण मिळते. त्यामुळे d = m2 + n2 + p2 + q2 ही संख्या घेतल्यास (a, b, c, d) हे पायथागोरसचे चतुष्क आपल्याला मिळते. अशी मिळवलेली सगळी चतुष्के आदिम नसली, तरी प्रत्येक आदिम चतुष्क, फार तर a, b, c यांची अदलाबदल करून, या रीतीने मिळवता येते. उदाहरणार्थ, आधीच्या रीतीने न मिळालेले (1, 2, 2, 3) हे आदिम त्रिक m = n = q = 1, p = 0 घेऊन मिळते; तसेच (3, 2, 6, 7) हे आदिम त्रिक m = p = q = 1, n = 2 घेऊन मिळवता येते. या विधानाची सिद्धता प्रथम लिओनार्ड डिक्सन (Leonard Dickson) या अमेरिकन गणितज्ञाने 1920 साली दिली, फ्रान्समधील स्त्रासबूर्ग (Strassbourg) या गावी भरलेल्या दुसऱ्या महायुद्धानंतरच्या पहिल्यावहिल्या आंतरराष्ट्रीय महासभेत (International Congress of Mathematicians). पायथागोरसच्या चतुष्कांचा एक गुणधर्म लक्षणीय आहे. जर (a, b, c, d) हे पायथागोरसचे चतुष्क असेल, तर a, b, c, d या चार संख्यांपैकी दोघींना तरी 2ने भाग जातो आणि एकीला तरी 3 ने भाग जातो. भाजक अंकगणित (दुवा) वापरून तर हे सिद्ध करणे सोयीस्कर ठरते. त्यामुळे abcd या चारी संख्यांच्या गुणाकाराला 12 ने नेहमीच भाग जातो. (1, 2, 2, 3) या सर्वात लहान चतुष्कासाठी तर हा गुणाकार बरोबर 12 आहे. समजा एका आयताकृती पेटीची लांबी, रुंदी, उंची a, b, c आहे, आणि ते तिन्ही पूर्णांक आहेत. जर तिच्या अवकाश कर्णाची लांबी d असेल, आणि तिच्या फलकांवरील कर्णांची लांबी p, q, r असेल, तर प्रश्न असा विचारू या की d, p, q, r हे चारही पूर्णांक असू शकतात का?

आपण आधी बघितल्याप्रमाणे फक्त अवकाश कर्णाची लांबी d पूर्णांकात हवी असेल तर a = 2, b = 2, c = 1 घेऊन काम भागते, कारण या छोट्या पेटीच्या अवकाश कर्णाची लांबी d = 3 असते; किंवा a = 6, b = 3, c = 2 घेऊनही काम भागते, कारण या जराशा मोठ्या पेटीच्या अवकाश कर्णाची लांबी d = 7 असते. जर फक्त फलकांवरील तीन कर्णांची लांबी p, q, r पूर्णांकात हवी असेल तर a = 240, b = 117, c = 44 या मोजमापाची अवाढव्य पेटी घ्यावी लागते. या पेटीच्या फलकांवरील कर्णांची लांबी p = 267, q = 125, r = 244 असते हे सहज पडताळून पाहता येते, कारण 2402 + 1172 = 2672, 1172 + 442 = 1252, 442 + 2402 = 2442. ही मनोरंजक आकडेमोड अठराव्या शतकापासून गणितज्ञांना माहित होती. पण d, p, q, r या चारही कर्णांची लांबी पूर्णांकात असणारी पेटी अजून कुणालाच सापडलेली नाही. उलटपक्षी अशी आयताकृती पेटी असूच शकणार नाही हे पण कुणाला सकारण दाखवता आलेले नाही. म्हणून आपला प्रश्न आजतागायत अनुत्तरित राहिला आहे. गणिती भाषेत हा प्रश्न असा आहे: a2 + b2 + c2, a2 + b2, b2 + c2 आणि c2 + a2 ह्या चारही संख्या पूर्ण वर्ग (perfect squares) होतील असे पूर्णांक a, b, c असतात की नसतात? पाहा तुमचे नशीब आजमावून किंवा गणिती कौशल्य पणाला लावून! दोन बिंदूंमधील अंतर इथपर्यंत आपण पायथागोरसच्या द्विमितीय आणि त्रिमितीय प्रमेयांची चर्चा केली. त्यांचा एक अतिशय महत्त्वाचा उपयोग आता पाहू. आपण नेहमी दोन जागांमधील किंवा दोन गोष्टींमधील किंवा दोन व्यक्तींमधील अंतरासंबंधी बोलत असतो. अशा गोष्टींचे प्रतिनिधित्व (representation) आपण बिंदूंनी करू या, व दोन बिंदूंमधील अंतर शोधून काढण्याचे सूत्र मिळवू या. त्यापूर्वी आपण द्विमितीय आणि त्रिमितीय भूमितीला बीजगणिताचे स्वरूप देणार आहोत. हे काम सर्वप्रथम फ्रान्समधील रेने देकार्त (René Descartes) या गणिती तत्त्ववेत्त्याने सतराव्या शतकाच्या मध्याला केले.

रेने दकार्तचे प्रतिमाचित्र
प्रतलावरील किंवा अवकाशातील बिंदूंचा दोन किंवा तीन संख्यांनी कसा निर्देश करायचा हे त्याने दाखवले. या संख्यांना त्या त्या बिंदूचे निर्देशांक (coordinates) असे म्हणतात, व त्यांचा वापर करणाऱ्या भूमितीला निर्देशक भूमिती (coordinate geometry) किंवा देकार्तची भूमिती (Cartesian geometry) असे नाव देतात. तिचा परिचय सध्या महाराष्ट्र राज्य पाठ्यपुस्तक निर्मिती मंडळाने प्रसिद्ध केलेल्या इयत्ता नववीच्या बालभारती या पुस्तकात करून दिला आहे. मात्र तिचा उपयोग करून मिळणारे दोन बिंदूंमधील अंतराचे सूत्र इयत्ता दहावीच्या दुसऱ्या भागापर्यंत लांबवले आहे. कुठे तरी सुरुवात तर केली पाहिजे म्हणून आपण एक विशिष्ट बिंदू निश्चित करू या व त्याला आरंभबिंदू (origin) असे नाव देऊ या. बहुतांशी तो O या अक्षराने दर्शवतात. प्रथम आपण फक्त एका आडव्या सरळ रेषेवरच वावरत आहोत असे समजू या व तिला संख्यारेषा मानू या. आपले बिंदू म्हणजे या रेषेवरील संख्या. सोयीसाठी आरंभबिंदू 0 (शून्य) या संख्येशी निगडित आहे मानू या. त्याच्या उजवीकडे धन संख्या व डावीकडे ऋण संख्या असतात. त्यांत -1, 1 सारखे पूर्णांक, -5/3 सारखे अपूर्णांक आणि √ 2 सारख्या अपरिमेय संख्या समाविष्ट आहेत.
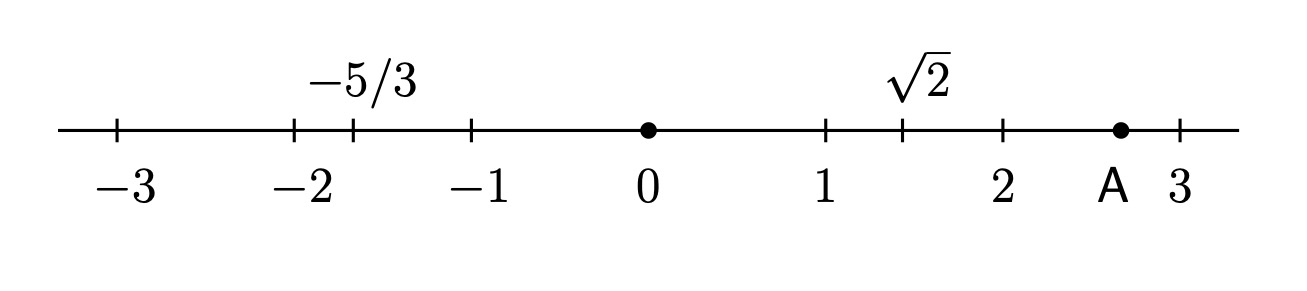
संख्यारेषा
रेषेवरील a या संख्येचे 0 या संख्येपासूनचे अंतर |a| या चिह्नाने दाखवतात व त्याला aचे केवल मूल्य (absolute value) असे म्हणतात. जर a ही संख्या धन असेल तर |a| = a आणि जर a ही संख्या ऋण असेल तर |a| = - a; जसे |3| = 3, पण |-3| = 3. यामुळे 0 या आरंभबिंदूपासूनचे अंतर कधीच ऋण नसते. (दुवा) दोन मितींचे प्रतल आता समजा आपण नुसत्या एका सपाट पृष्ठभागावर वावरत आहोत; त्याला प्रतल (plane) असे म्हणतात. प्रतलावरील A या बिंदूचा निर्देश आपण दोन संख्यांनी करणार आहोत.
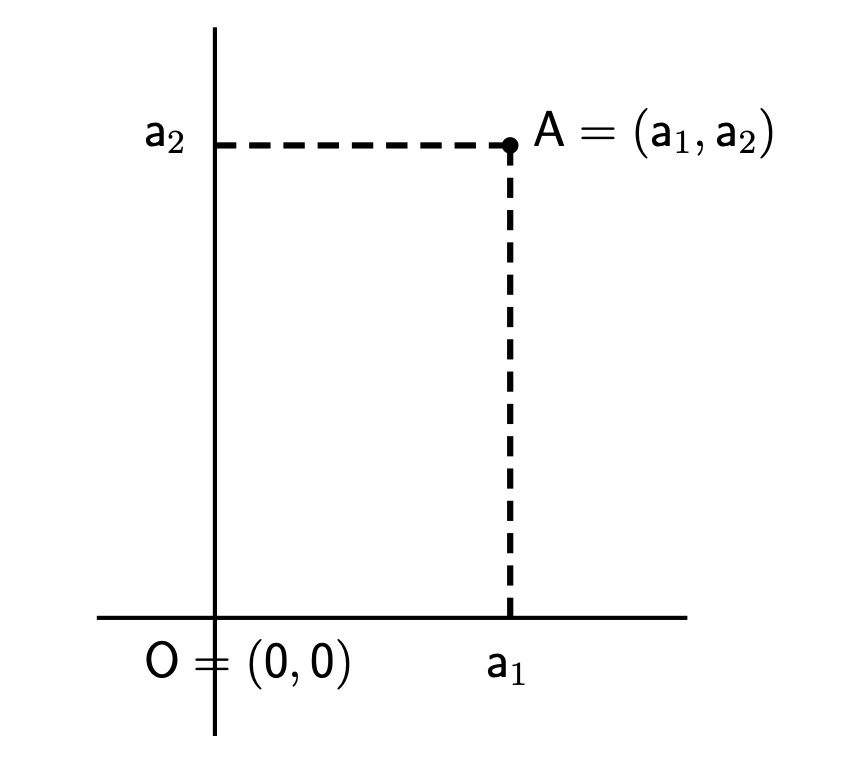
आपण आधी काढलेल्या आडव्या सरळ रेषेला काटकोन करणारी, व 0 या संख्येतून जाणारी एक उभी सरळ रेषा काढू या, व तिलाही संख्यारेषा मानू या. या दोन रेषा एकमेकींना प्रतलावरील ज्या बिंदूत छेदतात त्या बिंदूला आपण प्रतलावरील आरंभबिंदू मानू या, आणि त्याचा निर्देश O = (0, 0) असा करू या. समजा प्रतलावरील A या बिंदूपासून आडव्या संख्यारेषेवर टाकलेला लंब a1 या संख्येवर पडतो आणि उभ्या संख्यारेषेवर टाकलेला लंब a2 या संख्येवर पडतो. मग A या बिंदूचा निर्देश आपण A = (a1, a2) असा करायचा. या बिंदूचे आरंभबिंदूपासूनचे अंतर म्हणजे एका काटकोन त्रिकोणाच्या कर्णाची लांबी आहे, आणि त्या त्रिकोणाच्या इतर दोन बाजूंची लांबी आहे |a1| व |a2|. पायथागोरसच्या प्रमेयानुसार या कर्णाच्या लांबीचा वर्ग |a1|2 + |a2|2 , म्हणजेच a12 + a22, असला पाहिजे. प्रतलावरील A = (a1, a2) या बिंदूचे O = (0, 0) या आरंभबिंदूपासूनचे अंतर ||A|| या चिह्नाने दाखवण्याची पद्धत आहे. याप्रकारे पायथागोरसच्या प्रमेयाचा उपयोग करून आपल्याला
हे सूत्र मिळते. (दुवा) उदाहरणार्थ, A = (3, 4) यासाठी ||A|| = √ 32+42 = √ 25 = 5, तर B = (1, 2) यासाठी ||B|| = √ 12+22 = √ 5 . या सूत्राचा वापर करून आपण पायथागोरसचे प्रमेय वेगळ्या भाषेत मांडू शकतो. कसे ते आता पाहू. आपण नेहमी जशी a, b या संख्यांची बेरीज करून a + b अशी लिहितो, त्याप्रमाणे प्रतलावरील बिंदूंचीही बेरीज करता येते. समजा A = (a1, a2) आणि B = (b1, b2) हे प्रतलावरील बिंदू आहेत. त्यांची बेरीज अगदी स्वाभाविकपणे A + B = (a1 + b1, a2 + b2) अशी करायची, जसे (1, 2) + (3, 4) = (1 + 3, 2 + 4) = ( 4, 6).
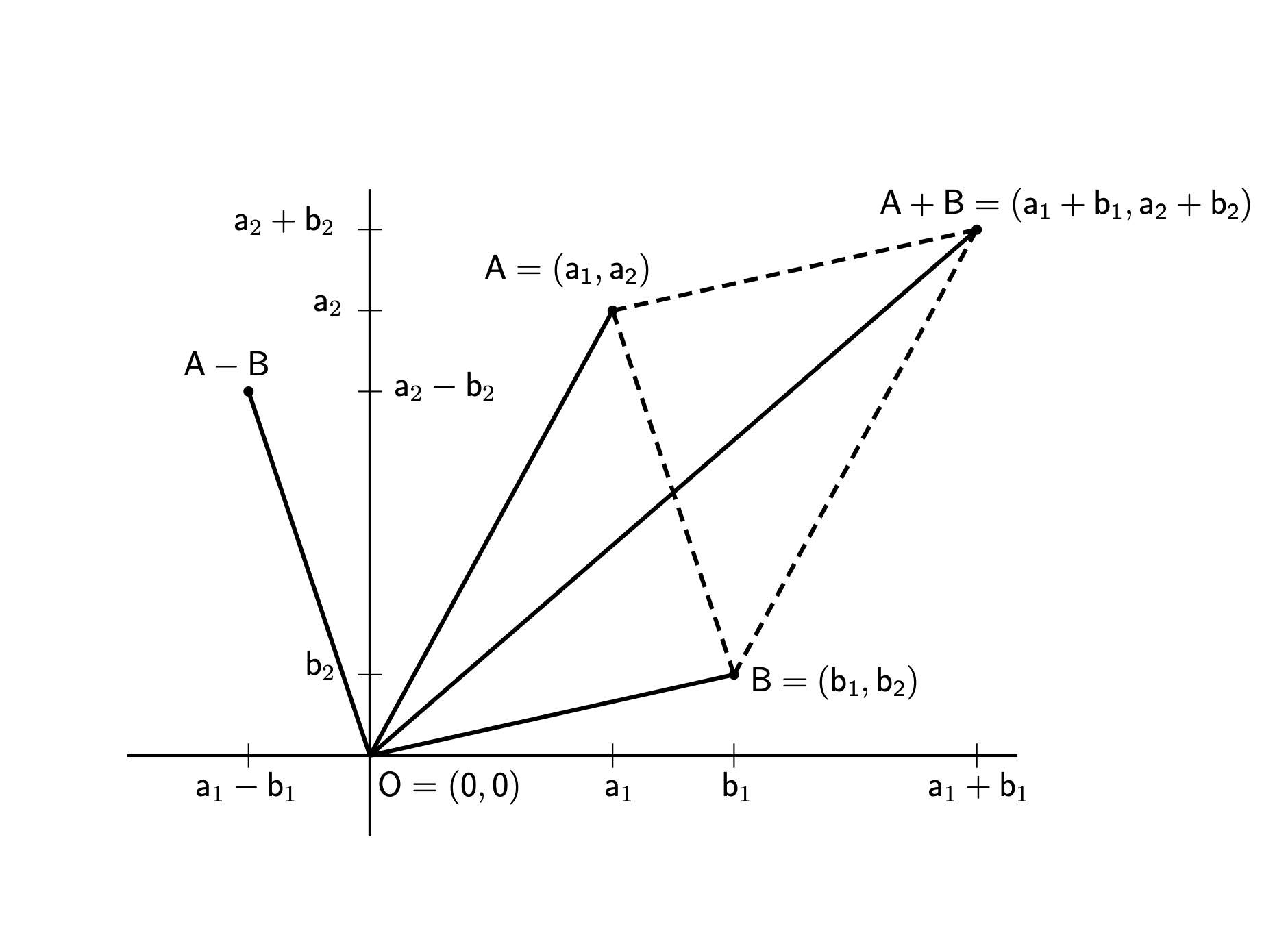
ही आकृती दाखवते की A + B हा बिंदू म्हणजे OA आणि OB या शेजारील बाजू असलेल्या समांतरभुज चौकोनाच्या (parallelogram) कर्णाचे दुसरे टोक आहे. (दुवा) आता A – B हा असा बिंदू असला पाहिजे की ज्याची आणि B या बिंदूची बेरीज केली की A हा बिंदू मिळेल, म्हणजे A - B = (a1 - b1, a2 - b2). वरील आकृतीत दाखवल्याप्रमाणे A आणि B या बिंदूंना जोडणारी रेषा O आणि A – B या बिंदूंना जोडणाऱ्या रेषेला समांतर असते. शिवाय त्या दोघींची लांबी तेवढीच, म्हणजे ||A - B|| असते. याचा अर्थ असा की A आणि B या प्रतलावरील बिंदूंमधील अंतर
या सूत्राने मिळते. उदाहरणार्थ, A = (3, 4) आणि B = (1, 2) या बिंदूंमधील तर आहे ||A - B|| = √ (3 -1)2 + (4 - 2)2 = √ 22 + 22 = √ 8 = 2√ 2 . एकमेकांशी काटकोन करणाऱ्या दोन रेषांपासून A हा बिंदू किती अंतरावर आहे, व तसेच B हा बिंदू किती अंतरावर आहे हे माहीत असले, तर या सूत्रामुळे आपण प्रतलावरील A व B या बिंदूंमधील अंतर शोधून काढू शकतो. त्यासाठी आपल्याला दोन संख्यांच्या बेरजेचे वर्गमूळ काढावे लागते. असे करणे नेहमीच सोपे नसते, हे खरे आहे. आता पायथागोरसचे प्रमेय आपल्याला सांगते की त्रिकोणाच्या OA आणि OB या बाजू जर एकमेकींशी काटकोन करत असतील तर ||A||2 + ||B||2 = ||A - B||2 हे समीकरण मिळते, आणि त्या प्रमेयाचा व्यत्यास आपल्याला सांगतो की जर ||A||2 + ||B||2 = ||A - B||2 हे समीकरण साधत असेल तर त्रिकोणाच्या OA आणि OB या बाजू एकमेकींशी काटकोन करतात. दोन्ही मिळून आपल्या पदरात पडते ते असे की ||A||2 + ||B||2 = ||A - B||2 हे समीकरण साधत असेल तेव्हाच त्रिकोणाच्या OA आणि OB या बाजू एकमेकींशी काटकोनात असतात. टिंब गुणाकार आणि काटकोन प्रतलावरील बिंदूंच्या बेरीज-वजाबाकीखेरीज एक वेगळ्या प्रकारचा गुणाकार उपयोगी ठरतो. A = (a1, a2) आणि B = (b1, b2) ह्या बिंदूंचा टिंब गुणाकार (dot product) A·B = a1b1 + a2b2 असा करायचा. उदाहरणार्थ, A = (3, 4) आणि B = (1, 2) या बिंदूंचा टिंब गुणाकार आहे A·B = 3 + 8 = 11. एक गोष्ट चटकन लक्षात येईल, ती म्हणजे जर B = A, म्हणजे b1 = a1, b2 = a2 असे असेल, तर A·A = a12 + a22 = ||A ||2. याचा अर्थ असा की एखाद्या बिंदूचा त्याच्याबरोबरच केलेला टिंब गुणाकार, आणि त्या बिंदूच्या आरंभबिंदूपासूनच्या अंतराचा वर्ग हे समान असतात. हा संबंध (relation) महत्त्वाचा आहे. आता ||A||2 = a12 + a22 , || B ||2 = b12 + b22 आणि ||A - B||2 = (a1 - b1)2 + (a2 - b2)2 = a12 + a22 + b12 + b22 - 2(a1b1 + a2b2) = ||A||2 + ||B||2 - 2 A·B. यावरून समजून येते की ||A||2 + ||B||2 = ||A - B||2 हे समीकरण तेव्हाच साधेल जेव्हा A·B = 0 असेल. आपण मघाच पाहिले की त्रिकोणाच्या OA आणि OB या बाजूंनी एकमेकींशी काटकोन करणे याचाच अर्थ ||A||2 + ||B||2 = ||A - B||2 हे समीकरण साधले जाणे. तात्पर्य, त्रिकोणाच्या OA आणि OB या बाजूंनी एकमेकींशी काटकोन करणे व A आणि B या बिंदूंचा टिंब गुणाकार A·B शून्य असणे या दोन गोष्टी अभिन्न (identical) आहेत, त्यांच्यात काही फरक नाही. असा मेळ असतो भूमिती आणि बीजगणित या दोहोंमध्ये!

उदाहरणार्थ, A = (-1, 1) आणि B = (1, 1), C = (1, 0) हे बिंदू घेतले तर, A·B = -1 + 1 = 0, व म्हणून OA आणि OB या दोन रेषा एकमेकींशी काटकोन करतात, पण B·C = 1 + 0 = 1, C·A = -1 + 0 = -1, व म्हणून OB आणि OC या दोन रेषा एकमेकींशी काटकोन करत नाहीत, व OC आणि OA या दोन रेषा एकमेकींशी काटकोन करत नाहीत. या तयारीनिशी आपल्याला पायथागोरसचे प्रमेय पुढीलप्रमाणे मांडता येते: A आणि B या प्रतलावरील बिंदूंचा टिंब गुणाकार जर शून्य असेल, तर ||A + B||2 = ||A||2 + ||B||2.
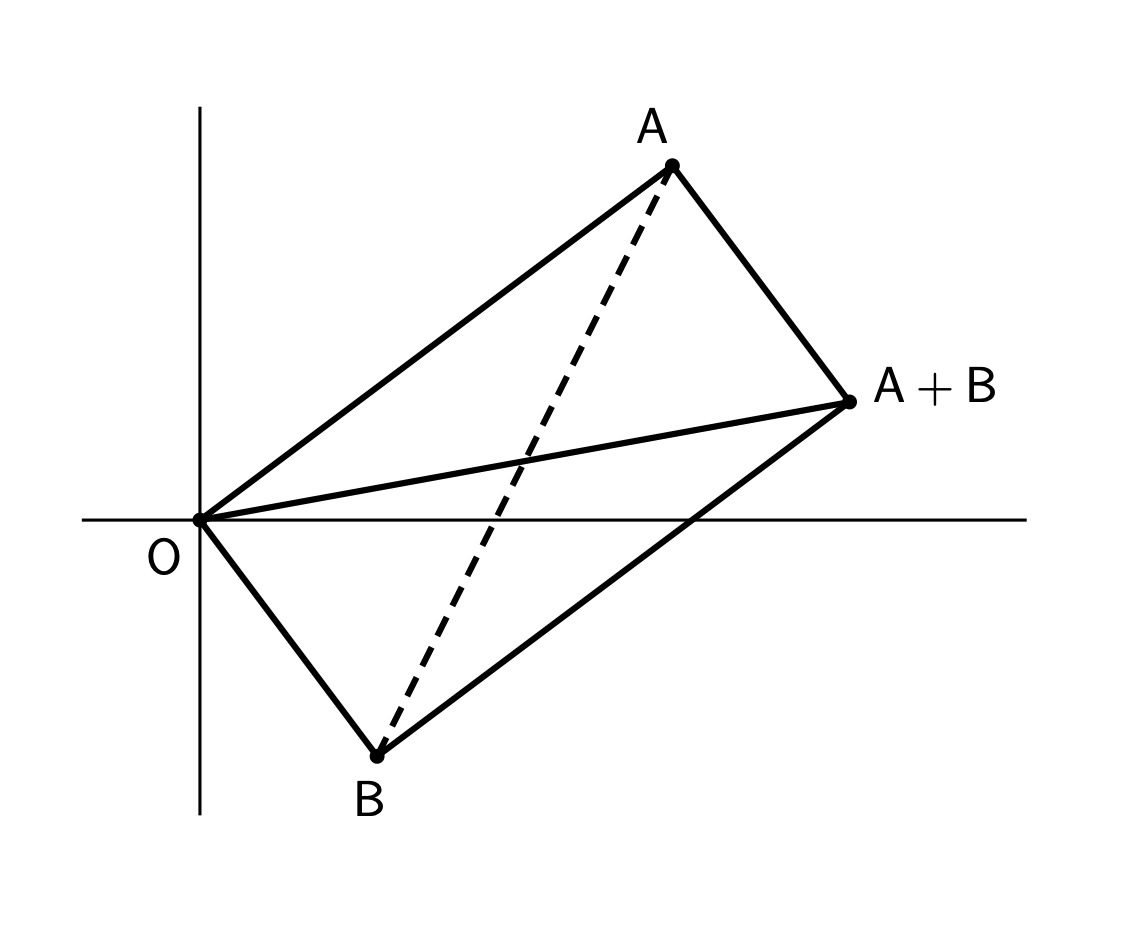
या प्रमेयाची बीजगणितावर आधारलेली सिद्धता सोपी आहे:
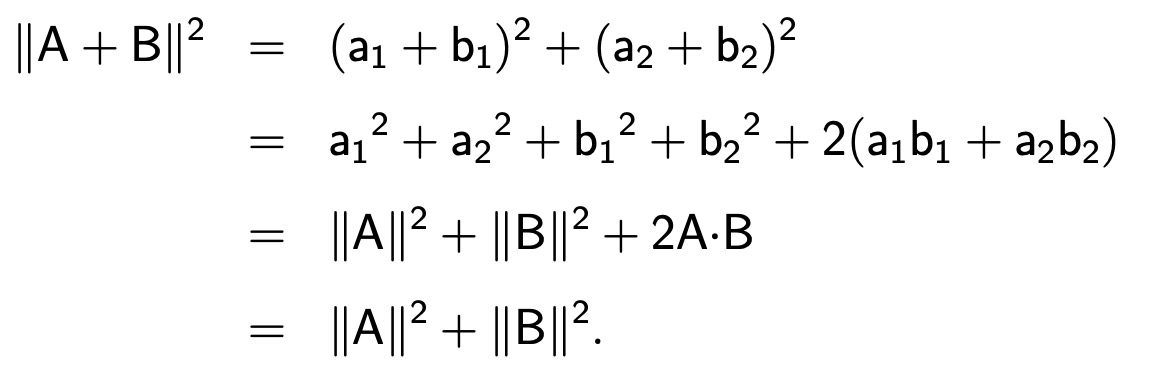
याचप्रमाणे पायथागोरसच्या प्रमेयाचा व्यत्यास पुढीलप्रमाणे मांडता येतो: A आणि B या प्रतलावरील बिंदूंसाठी || A + B||2 = ||A||2 + ||B||2 हे समीकरण साधत असेल तर त्या बिंदूंचा टिंब गुणाकार शून्य असतो. या व्यत्यासाची सिद्धता वर दिलेल्या सिद्धतेतच अंतर्भूत आहे. तीन मितींचे अवकाश अवकाशातील A या बिंदूचा निर्देश आपण तीन संख्यांनी करणार आहोत. आपण काढलेल्या आडव्या आणि उभ्या अशा दोन्ही सरळ रेषांना काटकोन करत (0, 0)मधून वर-खाली जाणारी एक तिसरी सरळ रेषा काढू या, व तिलाही संख्यारेषा मानू या. या तीन रेषा एकमेकींना ज्या बिंदूत छेदतात त्या बिंदूला आपण आरंभबिंदू मानू या, आणि त्याचा निर्देश O = (0, 0, 0) असा करू या. समजा अवकाशातील A या बिंदूपासून प्रतलावर टाकलेला लंब (a1, a2) या बिंदूवर पडतो आणि प्रतलाच्या वर-खाली जाणाऱ्या संख्यारेषेवर टाकलेला लंब a3 या संख्येवर पडतो. मग अवकाशातील A या बिंदूचा निर्देश आपण A = (a1, a2, a3) असा करायचा. या बिंदूचे आरंभबिंदूपासूनचे अंतर म्हणजे एका घनाभाच्या अवकाश कर्णाची लांबी आहे, आणि त्या घनाभाची लांबी, रुंदी, उंची आहे |a1|, |a2|, |a3|.
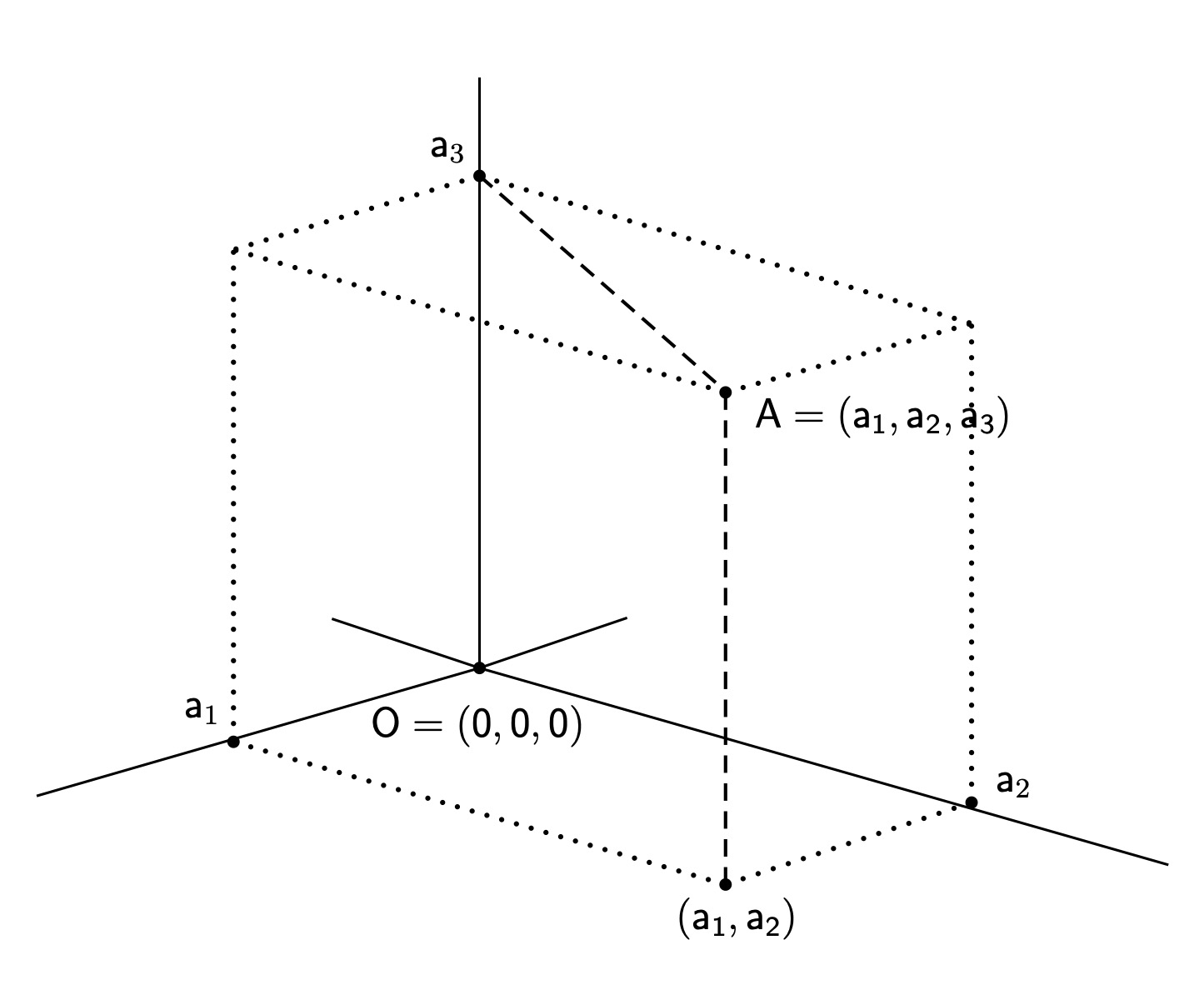
पायथागोरसच्या प्रमेयानुसार या अवकाश कर्णाच्या लांबीचा वर्ग |a1|2 + |a2|2 + |a3|2, म्हणजेच a12 + a22 + a32, असला पाहिजे. अवकाशातील A = (a1, a2, a3) या बिंदूचे O = (0, 0, 0) या आरंभबिंदूपासूनचे अंतरही ||A|| याच चिह्नाने दाखवण्याची पद्धत आहे. याप्रकारे पायथागोरसच्या प्रमेयाचा उपयोग करून आपल्याला
हे सूत्र मिळते. उदाहरणार्थ, A = (1, 2, 2) साठी ||A|| = √ 12 + 22 + 22 = √ 9 = 3, तर B = (1, 1, 1) साठी ||B|| = √ 12 + 12 + 12 = √ 3 . एकमेकांशी काटकोन करणाऱ्या तीन रेषांपासून A हा बिंदू किती अंतरावर आहे, व तसेच B हा बिंदू किती अंतरावर आहे हे माहीत असले, तर या सूत्रामुळे आपण अवकाशातील A व B या बिंदूंमधील अंतर शोधून काढू शकतो. आता समजा A = (a1, a2, a3) आणि B = (b1, b2, b3) हे अवकाशातील बिंदू आहेत. त्यांची बेरीज A + B = (a1 + b1, a2 + b2, a3 + b3) अशी करायची, प्रतलावरील बिंदूंच्या बेरजेसारखीच.
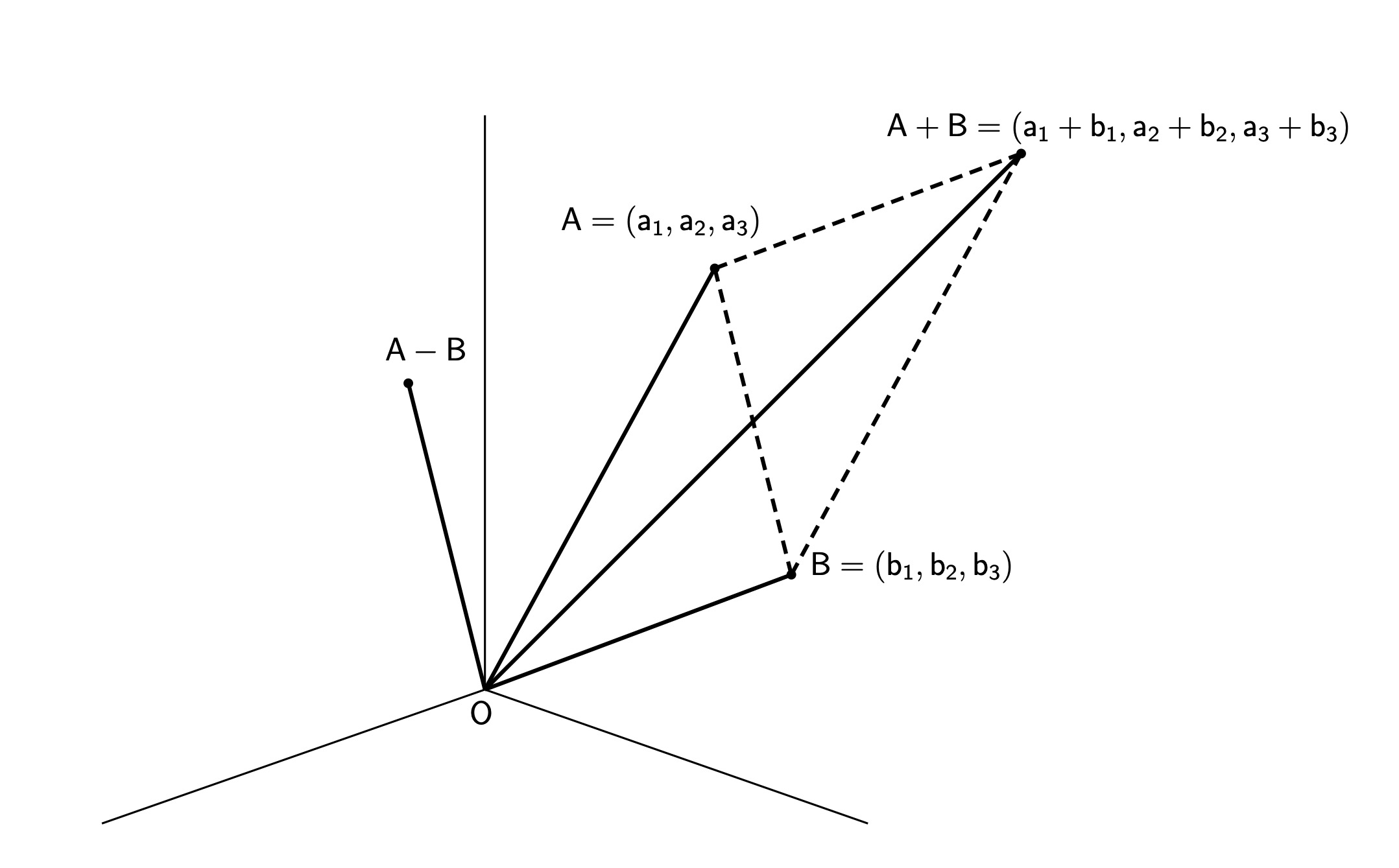
आधीप्रमाणेच A + B हा बिंदू म्हणजे OA आणि OB या शेजारील बाजू असलेल्या समांतरभुज चौकोनाच्या कर्णाचे दुसरे टोक आहे. तसेच वजाबाकी A - B = (a1 - b1, a2 - b2, a3 - b3) अशी करायची. त्यामुळे A आणि B या अवकाशातील बिंदूंमधील अंतर
या सूत्राने मिळते. उदाहरणार्थ, A = (1, 2, 2) आणि B = (1, 1, 1) या बिंदूंमधील अंतर आहे
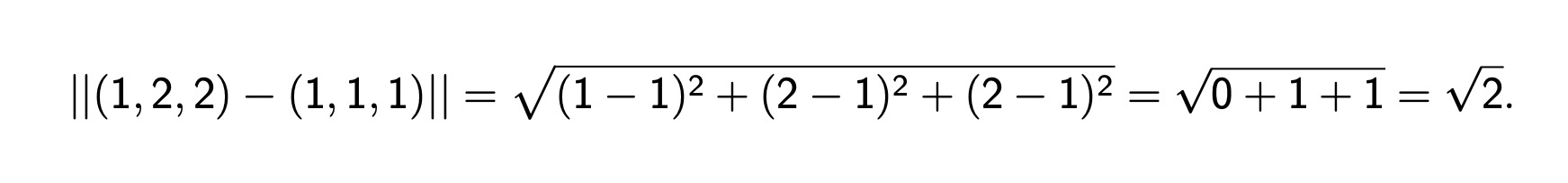
आता O, A, B, A + B आणि A - B हे अवकाशातील बिंदू एकाच प्रतलावर वास्तव्य करीत असल्याने OA आणि OB या बाजू असलेल्या त्रिकोणाला पायथागोरसचे द्विमितीय प्रमेय आणि त्याचा व्यत्यास लागू पडतो. त्यामुळे त्रिकोणाच्या OA आणि OB या बाजू एकमेकींशी तेव्हाच काटकोन करतील जेव्हा ||A||2 + ||B||2 = ||A - B||2 हे समीकरण साधत असेल. द्विमितीय बिंदूंप्रमाणेच A आणि B या त्रिमितीय बिंदूंचा टिंब गुणाकार A·B = a1b1 + a2b2 + a3b3 असा करायचा. उदाहरणार्थ, A = (1, 2, 2) आणि B = (1, 1, 1) या बिंदूंचा टिंब गुणाकार आहे A·B = 1 + 2 + 2 = 5. आता जर B = A, म्हणजे b1 = a1, b2 = a2, b3 = a3 असे असेल, तर A·A = a12 + a22 + a32 = ||A||2 हा महत्त्वाचा संबंध (relation) आपल्याला मिळतो, व त्यामुळे
||A - B||2 = a12 + a22 + a32 + b12 + b22 + b32- 2(a1b1 + a2b2 + a3b3) = ||A||2 + ||B||2 - 2 A·B.
हे समीकरण मिळते. यावरून समजून येते की ||A||2 + ||B||2 = ||A - B||2 हे समीकरण तेव्हाच साधेल जेव्हा A·B = 0. याचा अर्थ असा की त्रिकोणाच्या OA आणि OB या बाजूंनी एकमेकींशी काटकोन करणे व A आणि B या बिंदूंचा टिंब गुणाकार A·B शून्य असणे या दोन गोष्टींत काही फरक नाही, आधीप्रमाणेच.
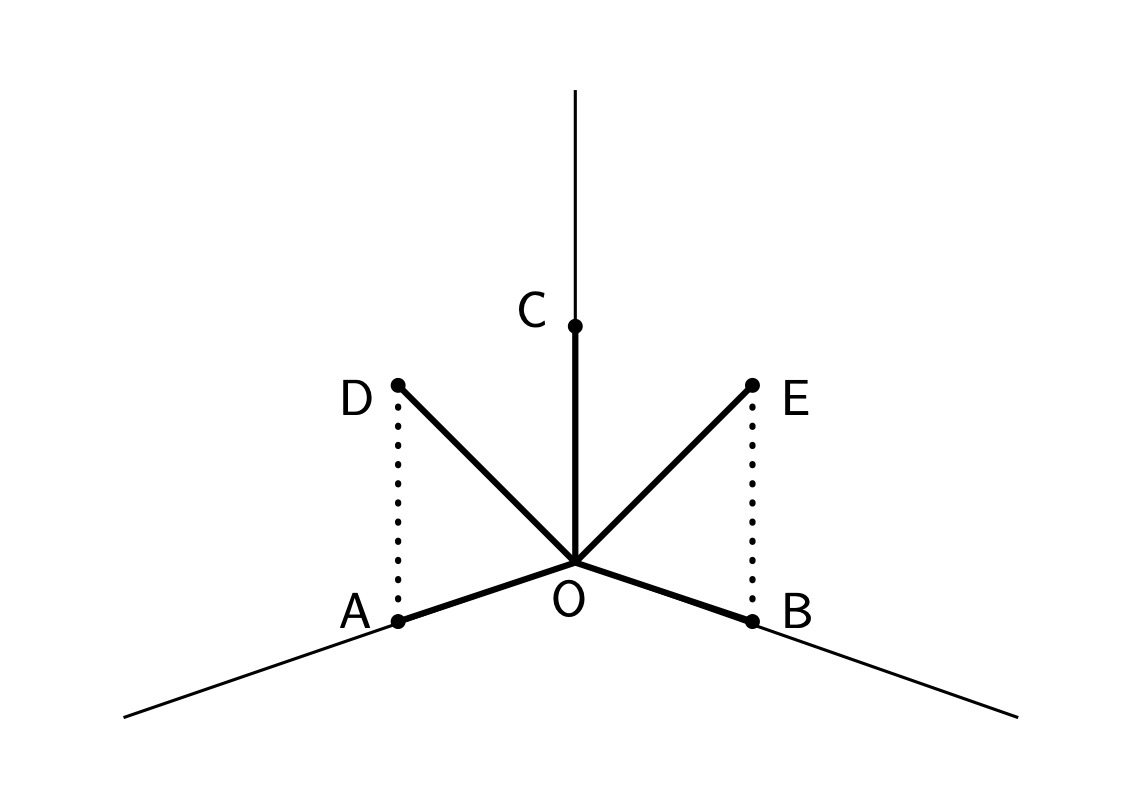
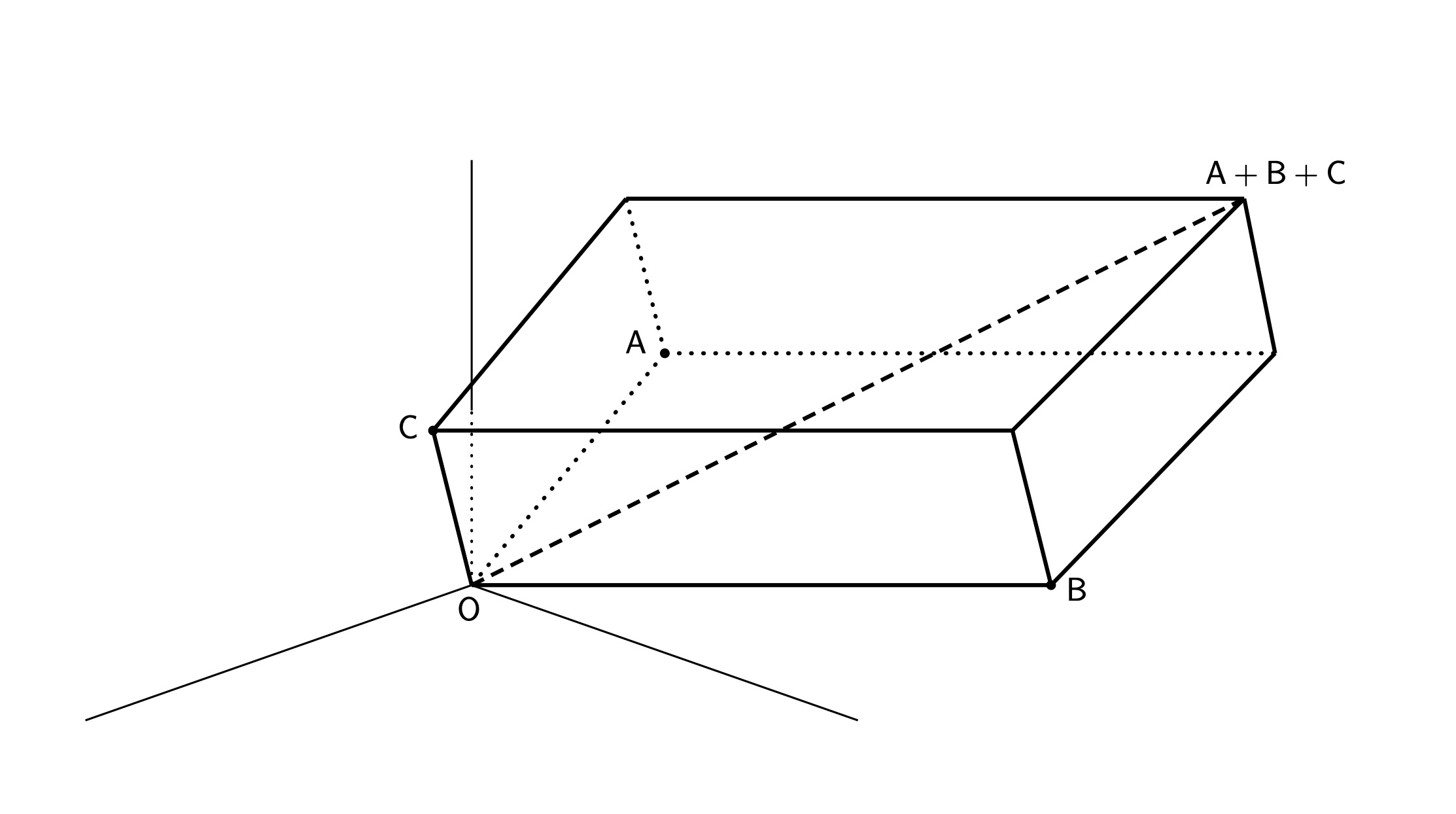
उदाहरणार्थ, जर A = (1, 0, 0), B = (0, 1, 0), C = (0, 0, 1) हे बिंदू घेतले, तर A·B = 0 + 0 + 0 = 0, व तसेच B·C = C·A = 0; म्हणून OA, OB, OC यांपैकी कुठल्याही दोन रेषा एकमेकींशी काटकोन करतात. पण D = (1, 0, 1) आणि E = (0, 1, 1) हे बिंदू घेतले, तर A·D = 1 + 0 + 0 = 1; म्हणून OA आणि OD या दोन रेषा एकमेकींशी काटकोन करत नाहीत, व B·E = 0 + 1 + 0 = 1; म्हणून OB आणि OE या दोन रेषा एकमेकींशी काटकोन करत नाहीत. आता समजा A , B, C हे अवकाशातील तीन बिंदू आहेत. मग A + B + C = (A + B ) + C हा बिंदू म्हणजे O या आरंभबिंदूपासून पासून A + B आणि C या दोन बिंदूंपर्यंत जाणाऱ्या सरळ रेषा शेजारील बाजू असलेल्या समांतरभुज चौकोनाच्या कर्णाचे दुसरे टोक आहे. तोच बिंदू आपल्याला B + C आणि A या दोन बिंदूंची बेरीज करून, व तसेच C + A आणि B या दोन बिंदूंची बेरीज करूनही मिळतो. अशाप्रकारे तयार होणारा समांतर षट्फलक (parallelepiped) खालील आकृतीत दाखवला आहे. त्याच्या सहा फलकांपैकी प्रत्येक फलक समांतरभुज चौकोन असतो; समोरासमोरील दोन चौकोन सारख्याच आकाराचे आणि एकमेकांना समांतर असतात. O या आरंभबिंदूपासून पासून A + B + C या बिंदूपर्यंत जाणारी सरळ रेषा या समांतर षट्फलकाचा एक अवकाश कर्ण असते.
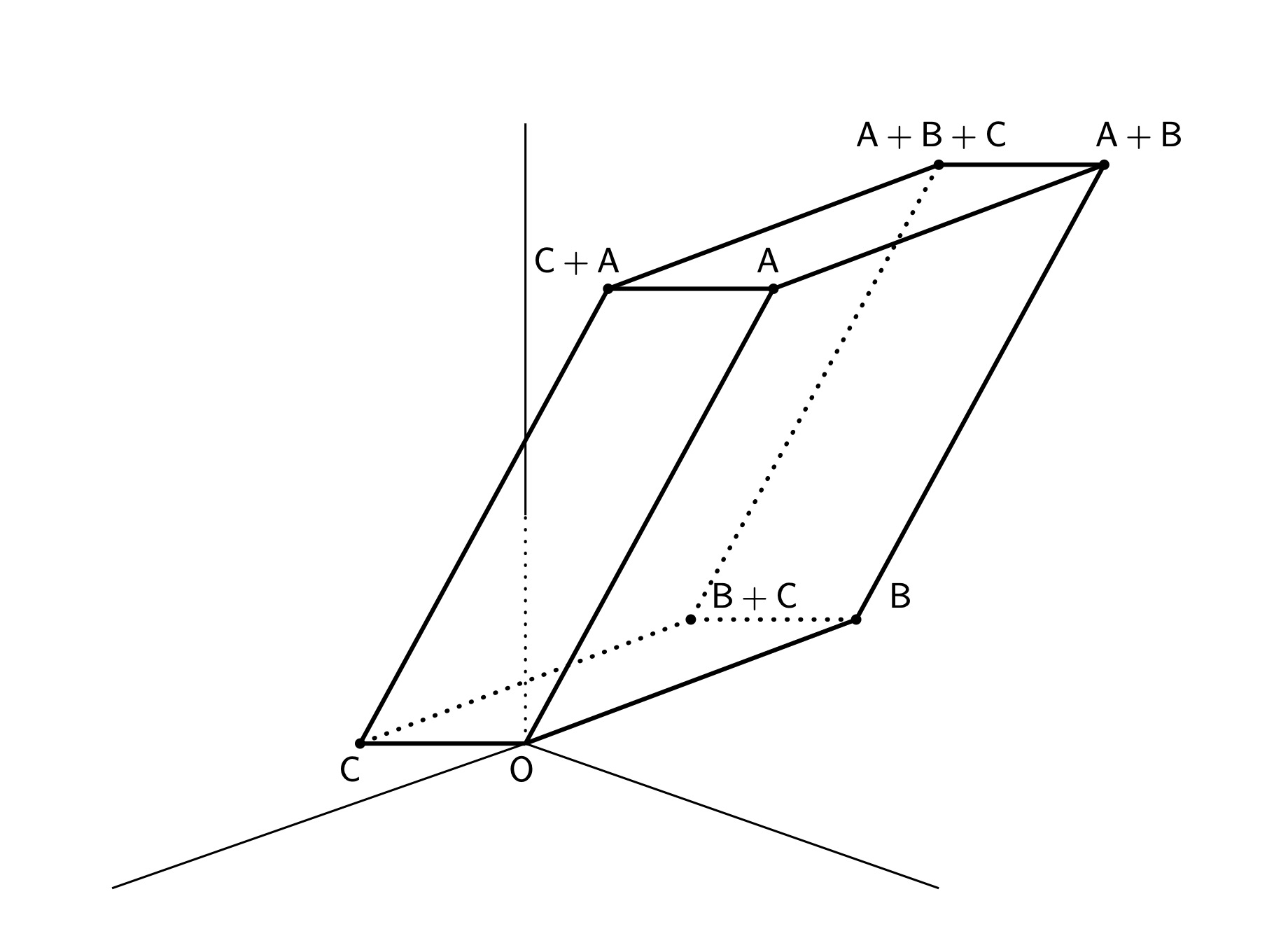
आता समजा की OA आणि OB काटकोनात आहेत, OB आणि OC काटकोनात आहेत, व OC आणि OA काटकोनात आहेत, म्हणजे OA, OB, OC यांपैकी प्रत्येकी दोन (pairwise) रेषा काटकोनात आहेत. मग आपल्याला ||A||, ||B||, ||C|| अशी लांबी, रुंदी, उंची असणारी एक आयताकृती पेटी म्हणजे घनाभ (cuboid) मिळतो. या घनाभाच्या अवकाश कर्णाची लांबी असते ||A + B + C||. पायथागोरसच्या त्रिमितीय प्रमेयानुसार ||A + B + C ||2 = ||A||2 + ||B||2 + || C ||2 असे समीकरण उपलब्ध होते. या प्रमेयाची भूमितीवर आधारलेली सिद्धता आपण पाहिलीच आहे. हेच प्रमेय आता पुढीलप्रमाणे मांडता येते. जर A, B, C या अवकाशातील बिंदूंपैकी प्रत्येकी दोन (pairwise) बिंदूंचा टिंब गुणाकार जर 0 असेल, तर ||A + B + C ||2 = ||A||2 + ||B||2 + || C ||2.
याची बीजगणितावर आधारलेली सिद्धता सोपी आहे.
||A + B + C ||2 = (a1 + b1 + c1)2 + (a2 + b2 + c2)2 + (a3 + b3 + c3)2 = ||A||2 + ||B||2 + || C ||2 + 2A·B + 2B·C + 2C·A = ||A||2 + ||B||2 + || C ||2
प्रतलावरील पायथागोरसच्या प्रमेयाचा व्यत्यास सत्य असल्याचे युक्लिडनेच सिद्ध केले होते. आता अवकाशातील पायथागोरसच्या प्रमेयाचा व्यत्यास सत्य आहे का, म्हणजे अवकाशातील A, B, C या बिंदूंसाठी ||A + B + C ||2 = ||A||2 + ||B||2 + || C ||2 हे समीकरण साधत असेल, तर A, B, C यांपैकी प्रत्येकी दोन बिंदूंचा टिंब गुणाकार शून्य असला पाहिजे का असा प्रश्न विचारू या. या प्रश्नाचे उत्तर नकारात्मक आहे. हे दाखवण्यासाठी फक्त एक उदाहरण दिले की पुरे. अवकाशात A = (1, 0, 0), B = (1, 0, 1) आणि C = (1, 1, -3) हे बिंदू घेतले, तर ||A||2 + ||B||2 + || C ||2 = 1 + 2 + 11 = 14. तसेच A + B + C = (3, 1, -2), आणि म्हणून ||A + B + C ||2 = 9 + 1 + 4 = 14; म्हणजे ||A + B + C ||2 = ||A||2 + ||B||2 + || C ||2, परंतु A·B = 1, B·C = -2 आणि C·A = 1 यांपैकी कुठलाही टिंब गुणाकार 0 नाही, म्हणजे OA, OB आणि OC यांपैकी कुठल्याही दोन रेषा काटकोनात नाहीत. या उदाहरणावरून आणि प्रमेयाच्या वर दिलेल्या बीजगणिती सिद्धतेवरून लक्षात येते की ||A + B + C ||2 = ||A||2 + ||B||2 + || C ||2 या निष्कर्षाप्रत येण्यासाठी A·B, B· C, C·A हे तिन्ही टिंब गुणाकार स्वतंत्रपणे शून्य असण्याची आवश्यकता नाही; फक्त त्यांची बेरीज A·B + B·C + C·A शून्य असली तरी पुरे आहे. पायथागोरसच्या त्रिमितीय प्रमेयाची आपण भौमितिक सिद्धता या लेखाच्या सुरुवातीला बघितली; तिच्यातही A·B = 0 व C·(A + B ) = 0, म्हणजे OA आणि OB या रेषा एकमेकींशी काटकोन करतात, व OC ही रेषा आणि O या आरंभबिंदूपासून A + Bपर्यंत जाणारी रेषा एकमेकींशी काटकोन करतात एवढेच वापरले आहे. पुढील भागात आपण तीनपेक्षा जास्त मिती असलेल्या विश्वांकडे मोर्चा वळवणार आहोत. आपले मार्गक्रमण सुकर होण्यासाठी या भागात विकसित केलेल्या यंत्रसामग्रीचा, म्हणजे निर्देशक भूमितीचा, भरपूर उपयोग करावा लागणार आहे. (क्रमशः) ---
बालमोहन लिमये
(balmohan.limaye@gmail.com)
लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण

लेख़ छान लिहीला आहे!
लेख़ छान लिहीला आहे!